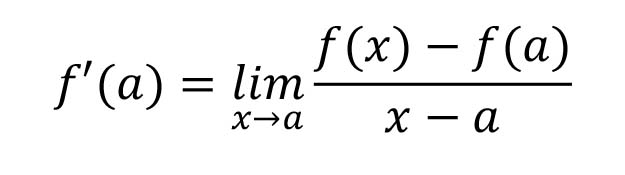The Infinite

Working with the infinite is tricky business. Zeno’s paradoxes first alerted Western philosophers to this in 450 B.C.E. when he argued that a fast runner such as Achilles has an infinite number of places to reach during the pursuit of a slower runner. Since then, there has been a struggle to understand how to use the notion of infinity in a coherent manner. This article concerns the significant and controversial role that the concepts of infinity and the infinite play in the disciplines of philosophy, physical science, and mathematics.

Philosophers want to know whether there is more than one coherent concept of infinity; which entities and properties are infinitely large, infinitely small, infinitely divisible, and infinitely numerous; and what arguments can justify answers one way or the other.

Here are some examples of these four different ways to be infinite. The density of matter at the center of a black hole is infinitely large. An electron is infinitely small. An hour is infinitely divisible. The integers are infinitely numerous. These four claims are ordered from most to least controversial, although all four have been challenged in the philosophical literature.

This article also explores a variety of other questions about the infinite. Is the infinite something indefinite and incomplete, or is it complete and definite? What did Thomas Aquinas mean when he said God is infinitely powerful? Was Gauss, who was one of the greatest mathematicians of all time, correct when he made the controversial remark that scientific theories involve infinities merely as idealizations and merely in order to make for easy applications of those theories, when in fact all physically real entities are finite? How did the invention of set theory change the meaning of the term “infinite”? What did Cantor mean when he said some infinities are smaller than others? Quine said the first three sizes of Cantor’s infinities are the only ones we have reason to believe in. Mathematical Platonists disagree with Quine. Who is correct? We shall see that there are deep connections among all these questions.

Table of Contents

1. What “Infinity” Means
   1. Actual, Potential, and Transcendental Infinity
   2. The Rise of the Technical Terms
2. Infinity and the Mind
3. Infinity in Metaphysics
4. Infinity in Physical Science
   1. Infinitely Small and Infinitely Divisible
   2. Singularities
   3. Idealization and Approximation
   4. Infinity in Cosmology
5. Infinity in Mathematics
   1. Infinite Sums
   2. Infinitesimals and Hyperreals
   3. Mathematical Existence
   4. Zermelo-Fraenkel Set Theory
   5. The Axiom of Choice and the Continuum Hypothesis
6. Infinity in Deductive Logic
   1. Finite and Infinite Axiomatizability
   2. Infinitely Long Formulas
   3. Infinitely Long Proofs
   4. Infinitely Many Truth Values
   5. Infinite Models
   6. Infinity and Truth
7. Conclusion
8. References and Further Reading

1. What “Infinity” Means

The term “the infinite” refers to whatever it is that the word “infinity” correctly applies to. For example, the infinite integers exist just in case there is an infinity of integers. We also speak of infinite quantities, but what does it mean to say a quantity is infinite? In 1851, Bernard Bolzano argued in The Paradoxes of the Infinite that, if a quantity is to be infinite, then the measure of that quantity also must be infinite. Bolzano’s point is that we need a clear concept of infinite number in order to have a clear concept of infinite quantity. This idea of Bolzano’s has led to a new way of speaking about infinity, as we shall see.

The term “infinite” can be used for many purposes. The logician Alfred Tarski used it for dramatic purposes when he spoke about trying to contact his wife in Nazi-occupied Poland in the early 1940s. He complained, “We have been sending each other an infinite number of letters. They all disappear somewhere on the way. As far as I know, my wife has received only one letter” (Feferman 2004, p. 137). Although the meaning of a term is intimately tied to its use, we can tell only a very little about the meaning of the term from Tarski’s use of it to exaggerate for dramatic effect.

Looking back over the last 2,500 years of use of the term “infinite,” three distinct senses stand out: actually infinite, potentially infinite, and transcendentally infinite. These will be discussed in more detail below, but briefly, the concept of potential infinity treats infinity as an unbounded or non-terminating process developing over time. By contrast, the concept of actual infinity treats the infinite as timeless and complete. Transcendental infinity is the least precise of the three concepts and is more commonly used in discussions of metaphysics and theology to suggest transcendence of human understanding or human capability.

To give some examples, the set of integers is actually infinite, and so is the number of locations (points of space) between London and Moscow. The maximum length of grammatical sentences in English is potentially infinite, and so is the total amount of memory in a Turing machine, an ideal computer. An omnipotent being’s power is transcendentally infinite.

For purposes of doing mathematics and science, the actual infinite has turned out to be the most useful of the three concepts. Using the idea proposed by Bolzano that was mentioned above, the concept of the actual infinite was precisely defined in 1888 when Richard Dedekind redefined the term “infinity” for use in set theory and Georg Cantor made the infinite, in the sense of infinite set, an object of mathematical study. Before this turning point, the philosophical community generally believed Aristotle’s concept of potential infinity should be the concept used in mathematics and science.

a. Actual, Potential, and Transcendental Infinity

The Ancient Greeks generally conceived of the infinite as formless, characterless, indefinite, indeterminate, chaotic, and unintelligible. The term had negative connotations and was especially vague, having no clear criteria for distinguishing the finite from the infinite. In his treatment of Zeno’s paradoxes about infinite divisibility, Aristotle (384-322 B.C.E.) made a positive step toward clarification by distinguishing two different concepts of infinity, potential infinity, and actual infinity. The latter is also called complete infinity and completed infinity. The actual infinite is not a process in time; it is an infinity that exists wholly at one time. By contrast, Aristotle spoke of the potentially infinite as a never-ending process over time, but which is finite at any specific time.

The word “potential” is being used in a technical sense. A potential swimmer can learn to become an actual swimmer, but a potential infinity cannot become an actual infinity. Aristotle argued that all the problems involving reasoning with infinity are really problems of improperly applying the incoherent concept of actual infinity instead of the coherent concept of potential infinity. (See Aristotle’s Physics, Book III, for his account of infinity.)

For its day, this was a successful way of treating Zeno’s Achilles paradox since, if Zeno had confined himself to using only potential infinity, he would not have been able to develop his paradoxical argument. Here is why. Zeno said that to go from the start to the finish line, the runner must reach the place that is halfway-there, then after arriving at this place he still must reach the place that is half of that remaining distance, and after arriving there he again must reach the new place that is now halfway to the goal, and so on. These are too many places to reach because there is no end to these places since for any one there is another. Zeno made the mistake, according to Aristotle, of supposing that this infinite process needs completing when it really doesn’t; the finitely long path from start to finish exists undivided for the runner, and it is Zeno the mathematician who is demanding the completion of such a process. Without that concept of a completed infinite process there is no paradox.

Although today’s standard treatment of the Achilles paradox disagrees with Aristotle and says Zeno was correct to use the concept of a completed infinity and to imply the runner must go to an actual infinity of places in a finite time, Aristotle had so many other intellectual successes that his ideas about infinity dominated the Western world for the next two thousand years.

Even though Aristotle promoted the belief that “the idea of the actual infinite−of that whose infinitude presents itself all at once−was close to a contradiction in terms…,” (Moore 2001, 40) during those two thousand years, others did not treat it as a contradiction in terms. Archimedes, Duns Scotus, William of Ockham, Gregory of Rimini, and Leibniz made use of it. Archimedes used it, but had doubts about its legitimacy. Leibniz used it but had doubts about whether it was needed.

Here is an example of how Gregory of Rimini argued in the fourteenth century for the coherence of the concept of actual infinity:

If God can endlessly add a cubic foot to a stone—which He can—then He can create an infinitely big stone. For He need only add one cubic foot at some time, another [cubic foot] half an hour later, another a quarter of an hour later than that, and so on ad infinitum. He would then have before Him an infinite stone at the end of the hour. (Moore 2001, 53)

Leibniz envisioned the world as being an actual infinity of mind-like monads, and in (Leibniz 1702) he freely used the concept of being infinitesimally small in his development of the calculus in mathematics.

The term “infinity” that is used in contemporary mathematics and science is based on a technical development of this earlier, informal concept of actual infinity. This technical concept was not created until late in the 19^th century.

b. The Rise of the Technical Terms

In the centuries after the decline of ancient Greece, the word “infinite” slowly changed its meaning in Medieval Europe. Theologians promoted the idea that God is infinite because He is limitless, and this at least caused the word “infinity” to lose its negative connotations. Eventually, during the Medieval Period, the word had come to mean endless, unlimited, and immeasurable–but not necessarily chaotic. The question of its intelligibility and conceivability by humans was disputed.

The term actual infinity is now very different. There are actual infinities in the technical, post-1880s sense, which are neither endless, unlimited, nor immeasurable. A line segment one meter long is a good example. It is not endless because it is finitely long, and it is not a process because it is timeless. It is not unlimited because it is limited by both zero and one. It is not immeasurable because its length measure is one meter. Nevertheless, the one-meter line is infinite in the technical sense because it has an actual infinity of sub-segments, and it has an actual infinity of distinct points. So, there definitely has been a conceptual revolution.

This can be very shocking to those people who are first introduced to the technical term “actual infinity.” It seems not to be the kind of infinity they are thinking about. The crux of the problem is that these people really are using a different concept of infinity. The sense of infinity in ordinary discourse these days is either the Aristotelian one of potential infinity or the medieval one that requires infinity to be endless, immeasurable, and perhaps to have connotations of perfection or inconceivability. This article uses the name transcendental infinity for the medieval concept although there is no generally accepted name for the concept. A transcendental infinity transcends human limits and detailed knowledge; it might be incapable of being described by a precise theory. It might also be a cluster of concepts rather than a single one.

Those people who are surprised when first introduced to the technical term “actual infinity” are probably thinking of either potential infinity or transcendental infinity, and that is why, in any discussion of infinity, some philosophers will say that an appeal to the technical term “actual infinity” is changing the subject. Another reason why there is opposition to actual infinities is that they have so many counter-intuitive properties. For example, consider a continuous line that has an actual infinity of points. A single point on this line has no next point! Also, a one-dimensional continuous curve can fill a two-dimensional area. Equally counterintuitive is the fact that some actually infinite numbers are smaller than other actually infinite numbers. Looked at more optimistically, though, most other philosophers will say the rise of this technical term is yet another example of how the discovery of a new concept has propelled civilization forward.

Resistance to the claim that there are actual infinities has had two other sources. One is the belief that actual infinities cannot be experienced. The other is the belief that use of the concept of actual infinity leads to paradoxes, such as Zeno’s. In order to solve Zeno’s Paradoxes, the standard solution makes use of calculus. The birth of the new technical definition of actual infinity is intimately tied to the development of calculus and thus to properly defining the mathematician’s real line, the linear continuum. The set of real numbers in their standard order was given the name “the continuum” or “the linear continuum” because it was believed that the real numbers fill up the entire number line continuously without leaving gaps. The integers have gaps, and so do the fractions.

Briefly, the argument for actual infinities is that science needs calculus; calculus needs the continuum; the continuum needs a very careful definition; and the best definition requires there to be actual infinities (not merely potential infinities) in the continuum.

Defining the continuum involves defining real numbers because the linear continuum is the intended model of the theory of real numbers just as the plane is the intended model of the theory of ordinary two-dimensional geometry. It was eventually realized by mathematicians that giving a careful definition to the continuum and to real numbers requires formulating their definitions within set theory. As part of that formulation, mathematicians found a good way to define a rational number in the language of set theory; then they defined a real number to be a certain pair of actually infinite sets of rational numbers. The continuum’s eventual definition required it to be an actually infinite collection whose elements are themselves infinite sets. The details are too complex to be presented here, but the curious reader can check any textbook in classical real analysis. The intuitive picture is that any interval or segment of the continuum is a continuum, and any continuum is a very special infinite set of points that are packed so closely together that there are no gaps. A continuum is perfectly smooth. This smoothness is reflected in there being a very great many real numbers between any two real numbers (technically a nondenumerable infinity between them).

Calculus is the area of mathematics that is more applicable to science than any other area. It can be thought of as a technique for treating a continuous change as being composed of an infinite number of infinitesimal changes. When calculus is applied to physical properties capable of change such as spatial location, ocean salinity, or an electrical circuit’s voltage, these properties are represented with continuous variables that have real numbers for their values. These values are specific real numbers, not ranges of real numbers and not just rational numbers. Achilles’ location along the path to his goal is such a property.

It took many centuries to rigorously develop the calculus. A very significant step in this direction occurred in 1888 when Richard Dedekind re-defined the term “infinity” and when Georg Cantor used that definition to create the first set theory, a theory that eventually was developed to the point where it could be used for embedding all classical mathematical theories. See the example in the Zeno’s Paradoxes article of how Dedekind used set theory and his new idea of “cuts” to define the real numbers in terms of infinite sets of rational numbers. In this way, additional rigor was given to the concepts of mathematics, and it encouraged more mathematicians to accept the notion of actually infinite sets. What this embedding requires is first defining the terms of any mathematical theory in the language of set theory, then translating the axioms and theorems of the mathematical theory into sentences of set theory, and then showing that these theorems follow logically from the axioms. (The axioms of any theory, such as set theory, are the special sentences of the theory that can always be assumed during the process of deducing the other theorems of the theory.)

The new technical treatment of infinity that originated with Dedekind in 1888 and was adopted by Cantor in his new set theory provided a definition of “infinite set” rather than simply “infinite.” Dedekind says an infinite set is a set that is not finite. The notion of a finite set can be defined in various ways. We might define it numerically as a set having n members, where n is some non-negative integer. Dedekind found an essentially equivalent definition of finite set (assuming the axiom of choice, which will be discussed later), but Dedekind’s definition does not require mentioning numbers:

A (Dedekind) finite set is a set for which there exists no one-to-one correspondence between it and one of its proper subsets.

By placing the finger-tips of your left hand on the corresponding fingertips of your right hand, you establish a one-to-one correspondence between the set of fingers of each hand; in that way, you establish that there is the same number of fingers on each of your hands, without your needing to count the fingers. More generally, there is a one-to-one correspondence between two sets when each member of one set can be paired off with a unique member of the other set, so that neither set has an unpaired member.

Here is a one-to-one correspondence between the natural numbers and its proper subset of even numbers, demonstrating that the natural numbers are infinite:

1	2	3	4	…
↕	↕	↕	↕
2	4	6	8	…

Informally expressed, any infinite set can be matched up to a part of itself; so the whole is equivalent to a part. This is a surprising definition because, before this definition was adopted, the idea that actually infinite wholes are equinumerous with some of their parts was taken as clear evidence that the concept of actual infinity is inherently paradoxical. For a systematic presentation of the many alternative ways to successfully define “infinite set” non-numerically, see (Tarski 1924).

Dedekind’s new definition of “infinite” is defining an actually infinite set, not a potentially infinite set because Dedekind appealed to no continuing operation over time. The concept of a potentially infinite set is then given a new technical definition by saying a potentially infinite set is a growing, finite subset of an actually infinite set. Cantor expressed the point this way:

In order for there to be a variable quantity in some mathematical study, the “domain” of its variability must strictly speaking be known beforehand through a definition. However, this domain cannot itself be something variable…. Thus this “domain” is a definite, actually infinite set of values. Thus each potential infinite…presupposes an actual infinite. (Cantor 1887)

The new idea is that the potentially infinite set presupposes an actually infinite one. If this is correct, then Aristotle’s two notions of the potential infinite and actual infinite have been redefined and clarified.

Two sets are the same if any member of one is a member of the other, and vice versa. Order of the members is irrelevant to the identity of the set, and to the size of the set. Two sets are the same size if there exists a one-to-one correspondence between them. This definition of same size was recommended by both Cantor and Frege. Cantor defined “finite” by saying a set is finite if there is a one-to-one correspondence with the set {1, 2, 3, …, n} for some positive integer n; and he said a set is infinite if it is not finite.

Cardinal numbers are measures of the sizes of sets. There are many definitions of what a cardinal number is, but what is essential for cardinal numbers is that two sets have the same cardinal just in case there is a one-to-one correspondence between them; and set A has a smaller cardinal number than a set B (and so set A has fewer members than B) provided there is a one-to-one correspondence between A and a subset of B, but B is not the same size as A. In this sense, the set of even integers does not have fewer members than the set of all integers, although intuitively you might think it does.

How big is infinity? This question does not make sense for either potential infinity or transcendental infinity, but it does for actual infinity. Finite cardinal numbers such as 0, 1, 2, and 3 are measures of the sizes of finite sets, and transfinite cardinal numbers are measures of the sizes of actually infinite sets. The transfinite cardinals are aleph-null, aleph-one, aleph-two, and so on; we represent them with the numerals ℵ₀, ℵ₁, ℵ₂, …. The smallest infinite size is ℵ₀ which is the size of the set of natural numbers, and it is said to be countably infinite (or denumerably infinite or enumerably infinite). The other alephs are measures of the uncountable infinities. However, calling a set of size ℵ₀ countably infinite is somewhat misleading since no process of counting is involved. Nobody would have the time to count from 0 to ℵ₀.

The set of even integers, the set of natural numbers and the set of rational numbers all can be shown to have the same size, but surprisingly they all are smaller than the set of real numbers. The set of points in the continuum and in any interval of the continuum turns out to be larger than ℵ₀, although how much larger is still an open problem, called the continuum problem. A popular but controversial suggestion is that a continuum is of size ℵ₁, the next larger size.

When creating set theory, mathematicians did not begin with the belief that there would be so many points between any two points in the continuum nor with the belief that for any infinite cardinal there is a larger cardinal. These were surprising consequences discovered by Cantor. To many philosophers, this surprise is evidence that what is going on is not invention but rather is discovery about mind-independent reality.

The intellectual community has always been wary of actually infinite sets. Before the discovery of how to embed calculus within set theory (a process that is also called giving calculus a basis in set theory), it could have been more easily argued that science does not need actual infinities. The burden of proof has now shifted, and the default position is that actual infinities are indispensable in mathematics and science, and anyone who wants to do without them must show that removing them does not do too much damage and has additional benefits. There are no known successful attempts to reconstruct the theories of mathematical physics without basing them on mathematical objects such as numbers and sets, but for one attempt to do so using second-order logic, see (Field 1980).

Here is why some mathematicians believe the set-theoretic basis is so important:

Just as chemistry was unified and simplified when it was realized that every chemical compound is made of atoms, mathematics was dramatically unified when it was realized that every object of mathematics can be taken to be the same kind of thing [namely, a set]. There are now other ways than set theory to unify mathematics, but before set theory there was no such unifying concept. Indeed, in the Renaissance, mathematicians hesitated to add x² to x³, since the one was an area and the other a volume. Since the advent of set theory, one can correctly say that all mathematicians are exploring the same mental universe. (Rucker 1982, p. 64)

But the significance of this basis can be exaggerated. The existence of the basis does not imply that mathematics is set theory.

Paradoxes soon were revealed within set theory—by Cantor himself and then others—so the quest for a more rigorous definition of the mathematical continuum continued. Cantor’s own paradox surfaced in 1895 when he asked whether the set of all cardinal numbers has a cardinal number. Cantor showed that, if it does, then it doesn’t. Surely the set of all sets would have the greatest cardinal number, but Cantor showed that for any cardinal number there is a greater cardinal number.  [For more details about this and the other paradoxes, see (Suppes 1960).] The most famous paradox of set theory is Russell’s Paradox of 1901. He showed that the set of all sets that are not members of themselves is both a member of itself and not a member of itself. Russell wrote that the paradox “put an end to the logical honeymoon that I had been enjoying.”

These and other paradoxes were eventually resolved satisfactorily by finding revised axioms of set theory that permit the existence of enough well-behaved sets so that set theory is not crippled [that is, made incapable of providing a basis for mathematical theories] and yet the axioms do not permit the existence of too many sets, the ill-behaved sets such as Cantor’s set of all cardinals and Russell’s set of all sets that are not members of themselves. Finally, by the mid-20^th century, it had become clear that, despite the existence of competing set theories, Zermelo-Fraenkel’s set theory (ZF) was the best way or the least radical way to revise set theory in order to avoid all the known paradoxes and problems while at the same time preserving enough of our intuitive ideas about sets that it deserved to be called a set theory, and at this time most mathematicians would have agreed that the continuum had been given a proper basis in ZF. See (Kleene 1967, pp. 189-191) for comments on this agreement about ZF’s success and for a list of the ZF axioms and for a detailed explanation of why each axiom deserves to be an axiom.

Because of this success, and because it was clear enough that the concept of infinity used in ZF does not lead to contradictions, and because it seemed so evident how to use the concept in other areas of mathematics and science where the term “infinity” was being used, the definition of the concept of “infinite set” within ZF was claimed by many philosophers to be the paradigm example of how to provide a precise and fruitful definition of a philosophically significant concept. Much less attention was then paid to critics who had complained that we can never use the word “infinity” coherently because infinity is ineffable or inherently paradoxical.

Nevertheless, there was, and still is, serious philosophical opposition to actually infinite sets and to ZF’s treatment of the continuum, and this has spawned the programs of constructivism, intuitionism, finitism, and ultrafinitism, all of whose advocates have philosophical objections to actual infinities. Even though there is much to be said in favor of replacing a murky concept with a clearer, technical concept, there is always the worry that the replacement is a change of subject that has not really solved the problems it was designed for. More discussion of the role of infinity in mathematics and science continues in later sections of this article.

2. Infinity and the Mind

Can humans grasp the concept of the infinite? This seems to be a profound question. Ever since Zeno, intellectuals have realized that careless reasoning about infinity can lead to paradox and perhaps “defeat” the human mind.

Some critics of infinity argue not just that paradox can occur but that paradox is essential to, or inherent in, the use of the concept of infinity, so the infinite is beyond the grasp of the human mind. However, this criticism applies more properly to some forms of transcendental infinity rather than to either actual infinity or potential infinity. This is a consequence of the development of set theory as we shall see in a later section.

A second reason to believe humans cannot grasp infinity is that the concept must contain an infinite number of sub-concepts, which is too many for our finite minds. A counter to this reason is to defend the psychological claim that if a person succeeds in thinking about infinity, it does not follow that the person needs to have an actually infinite number of ideas in mind at one time.

A third reason to believe the concept of infinity is beyond human understanding is that to have the concept one must have some accurate mental picture of infinity. Thomas Hobbes, who believed that all thinking is based on imagination, might remark that nobody could picture an infinite number of grains of sand at once. However, most contemporary philosophers of psychology believe mental pictures are not essential to have a concept. Regarding the concept of dog, you might have a picture of a brown dog in your mind, and I might have a picture of a black dog in mine, but I can still understand you perfectly well when you say dogs frequently chase cats.

The main issue here is whether we can coherently think about infinity to the extent of being said to have the concept. Here is a simple argument that we can: If we understand negation and have the concept of finite, then the concept of infinite is merely the concept of not-finite. A second argument says the apparent consistency of set theory indicates that infinity in the technical sense of actual infinity is well within our grasp. And since potential infinity is definable in terms of actual infinity, it, too, is within our grasp.

Assuming that infinity is within our grasp, what is it that we are grasping? Philosophers disagree on the answer. In 1883, the father of set theory, Georg Cantor, created a formal theory of infinite sets as a way of clarifying the infinite. This was a significant advance, but the notion of set can be puzzling. If you understand that a pencil is on my desk, must you implicitly understand that a set containing a pencil is on my desk? Plus a set containing that set? And another set containing the set containing the set with the pencil, and so forth to infinity?

In regard to mentally grasping an infinite set or any other set, Cantor said:

A set is a Many which allows itself to be thought of as a One.

Notice the dependence of a set upon thought. Cantor eventually clarified what he meant and was clear that he did not want set existence to depend on mental capability. What he really believed is that a set is a collection of well-defined and distinct objects that exist independently of being thought of, but that might be thought of by a powerful enough mind.

3. Infinity in Metaphysics

There is a concept which corrupts and upsets all others. I refer not to Evil, whose limited realm is that of ethics; I refer to the infinite. —Jorge Luis Borges.

Shakespeare declared, “The will is infinite.” Is he correct or just exaggerating? Critics of Shakespeare, interpreted literally, might argue that the will is basically a product of different brain states. Because a person’s brain contains approximately 10²⁷ atoms, these have only a finite number of configurations or states, and so, regardless of whether we interpret Shakespeare’s remark as implying that the will is unbounded (is potentially infinite) or the will produces an infinite number of brain states (is actually infinite), the will is not infinite. But perhaps Shakespeare was speaking metaphorically and did not intend to be taken literally, or perhaps he meant to use some version of transcendental infinity that makes infinity be somehow beyond human comprehension.

Contemporary Continental philosophers often speak that way. Emmanuel Levinas says the infinite is another name for the Other, for the existence of other conscious beings besides ourselves whom we are ethically responsible for. We “face the infinite” in the sense of facing a practically incomprehensible and unlimited number of possibilities upon encountering another conscious being. (See Levinas 1961.) If we ask what sense of “infinite” is being used by Levinas, it may be yet another concept of infinity, or it may be some kind of transcendental infinity. Another interpretation is that he is exaggerating about the number of possibilities and should say instead that there are too many possibilities to be faced when we encounter another conscious being and that the possibilities are not readily predictable because other conscious beings make free choices, the causes of which often are not known even to the person making the choice.

Leibniz was one of the few persons in earlier centuries who believed in actually infinite sets, but he did not believe in infinite numbers. Cantor did. Referring to his own discovery of the transfinite cardinals ℵ₀, ℵ₁, ℵ₂, …. and their properties, Cantor claimed his work was revealing God’s existence and that these mathematical objects were in the mind of God. He claimed God gave humans the concept of the infinite so that they could reflect on His perfection. Influential German neo-Thomists such as Constantin Gutberlet agreed with Cantor. Some Jesuit math instructors claim that by taking a calculus course and set theory course and understanding infinity, students are getting closer to God. Their critics complain that these mystical ideas about infinity and God are too speculative.

When metaphysicians speak of infinity they use all three concepts: potential infinity, actual infinity, and transcendental infinity. But when they speak about God being infinite, they are usually interested in implying that God is beyond human understanding or that there is a lack of a limit on particular properties of God, such as God’s goodness and knowledge and power.

The connection between infinity and God exists in nearly all of the world’s religions. It is prominent in Hindu, Muslim, Jewish, and Christian literature. For example, in chapter 11 of the Bhagavad Gita of Hindu scripture, Krishna says, “O Lord of the universe, I see You everywhere with infinite form….”

Plato did not envision God (the Demi-urge) as infinite because he viewed God as perfect, and he believed anything perfect must be limited and thus not infinite because the infinite was defined as an unlimited, unbounded, indefinite, unintelligible chaos.

But the meaning of the term “infinite” slowly began to change. Over six hundred years later, the Neo-Platonist philosopher Plotinus was one of the first important Greek philosophers to equate God with the infinite−although he did not do so explicitly. He said instead that any idea abstracted from our finite experience is not applicable to God. He probably believed that if God were finite in some aspect, then there could be something beyond God and therefore God wouldn’t be “the One.” Plotinus was influential in helping remove the negative connotations that had accompanied the concept of the infinite. One difficulty here, though, is that it is unclear whether metaphysicians have discovered that God is identical with the transcendentally infinite or whether they are simply defining “God” to be that way. A more severe criticism is that perhaps they are just defining “infinite” (in the transcendental sense) as whatever God is.

Augustine, who merged Platonic philosophy with the Christian religion, spoke of God “whose understanding is infinite” for “what are we mean wretches that dare presume to limit His knowledge?” Augustine wrote that the reason God can understand the infinite is that “…every infinity is, in a way we cannot express, made finite to God….” [City of God, Book XII, ch. 18] This is an interesting perspective. Medieval philosophers debated whether God could understand infinite concepts other than Himself, not because God had limited understanding, but because there was no such thing as infinity anywhere except in God.

The medieval philosopher Thomas Aquinas, too, said God has infinite knowledge. He definitely did not mean potentially infinite knowledge. The technical definition of actual infinity might be useful here. If God is infinitely knowledgeable, this can be understood perhaps as meaning that God knows the truth values of all declarative sentences and that the set of these sentences is actually infinite.

Aquinas argued in his Summa Theologia that, although God created everything, nothing created by God can be actually infinite. His main reason was that anything created can be counted, yet if an infinity were created, then the count would be infinite, but no infinite numbers exist to do the counting (as Aristotle had also said). In his day this was a better argument than today because Cantor created (or discovered) infinite numbers in the late 19^th century.

René Descartes believed God was actually infinite, and he remarked that the concept of actual infinity is so awesome that no human could have created it or deduced it from other concepts, so any idea of infinity that humans have must have come from God directly. Thus God exists. Descartes is using the concept of infinity to produce a new ontological argument for God’s existence.

David Hume, and many other philosophers, raised the problem that if God has infinite power then there need not be evil in the world, and if God has infinite goodness, then there should not be any evil in the world. This problem is often referred to as “The Problem of Evil” and has been a long-standing point of contention for theologians.

Spinoza and Hegel envisioned God, or the Absolute, pantheistically. If they are correct, then to call God infinite, is to call the world itself infinite. Hegel denigrated Aristotle’s advocacy of potential infinity and claimed the world is actually infinite. Traditional Christian, Muslim, and Jewish metaphysicians do not accept the pantheistic notion that God is at one with the world. Instead, they say God transcends the world. Since God is outside space and time, the space and time that he created may or may not be infinite, depending on God’s choice, but surely everything else he created is finite, they say.

The multiverse theories of cosmology in the early 21^st century allow there to be an uncountable infinity of universes within a background space whose volume is actually infinite. The universe created by our Big Bang is just one of these many universes. Christian theologians often balk at the notion of God choosing to create this multiverse because the theory’s implication that, although there are so many universes radically different from ours, there also are an actually infinite number of ones just like ours. This implies there is an infinite number of indistinguishable copies of Jesus, each of whom has been crucified on the cross. This removal of the uniqueness of Jesus is apparently a removal of his dignity. Augustine had this worry about uniqueness when considering infinite universes, and he responded that “Christ died once for sinners….”

There are many other entities and properties that some metaphysician or other has claimed are infinite: places, possibilities, propositions, properties, particulars, partial orderings, pi’s decimal expansion, predicates, proofs, Plato’s forms, principles, power sets, probabilities, positions, and possible worlds. That is just for the letter p. Some of these are considered to be abstract objects, objects outside of space and time, and others are considered to be concrete objects, objects within, or part of, space and time.

For helpful surveys of the history of infinity in theology and metaphysics, see (Owen 1967) and (Moore 2001).

4. Infinity in Physical Science

From a metaphysical perspective, the theories of mathematical physics seem to be ontologically committed to objects and their properties. If any of those objects or properties are infinite, then physics is committed to there being infinity within the physical world.

Here are four suggested examples where infinity occurs within physical science. (1) Standard cosmology based on Einstein’s general theory of relativity implies the density of the mass at the center of a simple black hole is infinitely large (even though the black hole’s total mass is finite). (2) The Standard Model of particle physics implies the size of an electron is infinitely small. (3) General relativity implies that every path in space is infinitely divisible. (4) Classical quantum theory implies the values of the kinetic energy of an accelerating, free electron are infinitely numerous. These four kinds of infinities—infinite large, infinitely small, infinitely divisible, and infinitely numerous—are implied by theory and argumentation, and are not something that could be measured directly.

Objecting to taking scientific theories at face value, the 18th-century British empiricists George Berkeley and David Hume denied the physical reality of even potential infinities on the empiricist grounds that such infinities are not detectable by our sense organs. Most philosophers of the 21^st century would say that Berkeley’s and Hume’s empirical standards are too rigid because they are based on the mistaken assumption that our knowledge of reality must be a complex built up from simple impressions gained from our sense organs.

But in the spirit of Berkeley’s and Hume’s empiricism, instrumentalists also challenge any claim that science tells us the truth about physical infinities. The instrumentalists say that all theories of science are merely effective “instruments” designed for explanatory and predictive success. A scientific theory’s claims are neither true nor false. By analogy, a shovel is an effective instrument for digging, but a shovel is neither true nor false. The instrumentalist would say our theories of mathematical physics imply only that reality looks “as if” there are physical infinities. Some realists on this issue respond that to declare it to be merely a useful mathematical fiction that there are physical infinities is just as misleading as to say it is mere fiction that moving planets actually have inertia or petunias actually contain electrons. We have no other tool than theory-building for accessing the existing features of reality that are not directly perceptible. If our best theories—those that have been well tested and are empirically successful and make novel predictions—use theoretical terms that refer to infinities, then infinities must be accepted. See (Leplin 2000) for more details about anti-realist arguments, such as those of instrumentalism and constructive empiricism.

a. Infinitely Small and Infinitely Divisible

Consider the size of electrons and quarks, the two main components of atoms. All scientific experiments so far have been consistent with electrons and quarks having no internal structure (components), as our best scientific theories imply, so the “simple conclusion” is that electrons are infinitely small, or infinitesimal, and zero-dimensional. Is this “simple conclusion” too simple? Some physicists speculate that there are no physical particles this small and that, in each subsequent century, physicists will discover that all the particles of the previous century have a finite size due to some inner structure. However, most physicists withhold judgment on this point about the future of physics.

A second reason to question whether the “simple conclusion” is too simple is that electrons, quarks, and all other elementary particles behave in a quantum mechanical way. They have a wave nature as well as a particle nature, and they have these simultaneously. When probing an electron’s particle nature it is found to have no limit to how small it can be, but when probing the electron’s wave nature, the electron is found to be spread out through all of space, although it is more probably in some places than others. Also, quantum theory is about groups of objects, not a single object. The theory does not imply a definite result for a single observation but only for averages over many observations, so this is why quantum theory introduces inescapable randomness or unpredictability into claims about single objects and single experimental results. The more accurate theory of quantum electrodynamics (QED) that incorporates special relativity and improves on classical quantum theory for the smallest regions, also implies electrons are infinitesimal particles when viewed as particles, while they are wavelike or spread out when viewed as waves. When considering the electron’s particle nature, QED’s prediction of zero volume has been experimentally verified down to the limits of measurement technology. The measurement process is limited by the fact that light or other electromagnetic radiation must be used to locate the electron, and this light cannot be used to determine the position of the electron more accurately than the distance between the wave crests of the light wave used to bombard the electron. So, all this is why the “simple conclusion” mentioned at the beginning of this paragraph may be too simple. For more discussion, see the chapter “The Uncertainty Principle” in (Hawking 2001) or (Greene 1999, pp. 121-2).

If a scientific theory implies space is a continuum, with the structure of a mathematical continuum, then if that theory is taken at face value, space is infinitely divisible and composed of infinitely small entities, the so-called points of space. But should it be taken at face value? The mathematician David Hilbert declared in 1925, “A homogeneous continuum which admits of the sort of divisibility needed to realize the infinitely small is nowhere to be found in reality. The infinite divisibility of a continuum is an operation which exists only in thought.” Hilbert said actual, transcendental infinities are real in mathematics, but not in physics. Many physicists agree with Hilbert. Many other physicists and philosophers argue that, although Hilbert is correct that ordinary entities such as strawberries and cream are not continuous, he is ultimately incorrect, for the following reasons.

First, the Standard Model of particles and forces is one of the best tested and most successful theories in all the history of physics. So are the theories of relativity and quantum mechanics. All these theories imply or assume that, using Cantor’s technical sense of actual infinity, there are infinitely many infinitesimal instants in any non-zero duration, and there are infinitely many point places along any spatial path. So, time is a continuum, and space is a continuum.

The second challenge to Hilbert’s position is that quantum theory, in agreement with relativity theory, implies that for any possible kinetic energy of a free electron there is half that energy−insofar as an electron can be said to have a value of energy independent of being measured to have it. Although the energy of an electron bound within an atom is quantized, the energy of an unbound or free electron is not. If it accelerates in its reference frame from zero to nearly the speed of light, its energy changes and takes on all intermediate real-numbered values from its rest energy to its total energy. But mass is just a form of energy, as Einstein showed in his famous equation E = mc², so in this sense mass is a continuum as well as energy.

How about non-classical quantum mechanics, the proposed theories of quantum gravity that are designed to remove the disagreements between quantum mechanics and relativity theory? Do these non-classical theories quantize all these continua we’ve been talking about? One such theory, the theory of loop quantum gravity, implies space consists of discrete units called loops. But string theory, which is the more popular of the theories of quantum gravity in the early 21^st century, does not imply space is discontinuous. [See (Greene 2004) for more details.] Speaking about this question of continuity, the theoretical physicist Brian Greene says that, although string theory is developed against a background of continuous spacetime, his own insight is that

[T]he increasingly intense quantum jitters that arise on decreasing scales suggest that the notion of being able to divide distances or durations into ever smaller units likely comes to an end at around the Planck length (10^-33centimeters) and Planck time (10^-43 seconds). …There is something lurking in the microdepths−something that might be called the bare-bones substrate of spacetime−the entity to which the familiar notion of spacetime alludes. We expect that this ur-ingredient, this most elemental spacetime stuff, does not allow dissection into ever smaller pieces because of the violent fluctuations that would ultimately be encountered…. [If] familiar spacetime is but a large-scale manifestation of some more fundamental entity, what is that entity and what are its essential properties? As of today, no one knows. (Greene 2004, pp. 473, 474, 477)

Disagreeing, the theoretical physicist Roger Penrose speaks about both loop quantum gravity and string theory and says:

…in the early days of quantum mechanics, there was a great hope, not realized by future developments, that quantum theory was leading physics to a picture of the world in which there is actually discreteness at the tiniest levels. In the successful theories of our present day, as things have turned out, we take spacetime as a continuum even when quantum concepts are involved, and ideas that involve small-scale spacetime discreteness must be regarded as ‘unconventional.’ The continuum still features in an essential way even in those theories which attempt to apply the ideas of quantum mechanics to the very structure of space and time…. Thus it appears, for the time being at least, that we need to take the use of the infinite seriously, particular in its role in the mathematical description of the physical continuum. (Penrose 2005, 363)

b. Singularities

There is a good reason why scientists fear the infinite more than mathematicians do. Scientists have to worry that someday we will have a dangerous encounter with a singularity, with something that is, say, infinitely hot or infinitely dense. For example, we might encounter a singularity by being sucked into a black hole. According to Schwarzschild’s solution to the equations of general relativity, a simple, non-rotating black hole is infinitely dense at its center. For a second example of where there may be singularities, there is good reason to believe that 13.8 billion years ago the entire universe was a singularity with infinite temperature, infinite density, infinitesimal volume, and infinite curvature of spacetime.

Some philosophers will ask: Is it not proper to appeal to our best physical theories in order to learn what is physically possible? Usually, but not in this case, say many scientists, including Albert Einstein. He believed that, if a theory implies that some physical properties might have or, worse yet, do have actually infinite values (the so-called singularities), then this is a sure sign of error in the theory. It’s an error primarily because the theory will be unable to predict the behavior of the infinite entity, and so the theory will fail. For example, even if there were a large, shrinking universe pre-existing the Big Bang, if the Big Bang were considered to be an actual singularity, then knowledge of the state of the universe before the Big Bang could not be used to predict events after the Big Bang, or vice versa. This failure to imply the character of later states of the universe is what Einstein’s collaborator Peter Bergmann meant when he said, “A theory that involves singularities…carries within itself the seeds of its own destruction.” The majority of physicists probably would agree with Einstein and Bergmann about this, but the critics of these scientists say this belief that we need to remove singularities everywhere is merely a hope that has been turned into a metaphysical assumption.

But doesn’t quantum theory also rule out singularities? Yes. Quantum theory allows only arbitrary large, finite values of properties such as temperature and mass-energy density. So which theory, relativity theory or quantum theory, should we trust to tell us whether the center of a black hole is or isn’t a singularity? The best answer is, “Neither, because we should get our answer from a theory of quantum gravity.” A principal attraction of string theory, a leading proposal for a theory of quantum gravity to replace both relativity theory and quantum theory, is that it eliminates the many singularities that appear in previously accepted physical theories such as relativity theory. In string theory, the electrons and quarks are not point particles but are small, finite loops of fundamental string. That finiteness in the loop is what eliminates the singularities.

Unfortunately, string theory has its own problems with infinity. It implies an infinity of kinds of particles. If a particle is a string, then the energy of the particle should be the energy of its vibrating string. Strings have an infinite number of possible vibrational patterns each corresponding to a particle that should exist if we take the theory literally. One response that string theorists make to this problem about too many particles is that perhaps the infinity of particles did exist at the time of the Big Bang but now they have all disintegrated into a shower of simpler particles and so do not exist today. Another response favored by string theorists is that perhaps there never were an infinity of particles nor a Big Bang singularity in the first place. Instead, the Big Bang was a Big Bounce or quick expansion from a pre-existing, shrinking universe whose size stopped shrinking when it got below the critical Planck length of about 10^-35 meters.

c. Idealization and Approximation

Scientific theories use idealization and approximation; they are “lies that help us to see the truth,” to use a phrase from the painter Pablo Picasso (who was speaking about art, not science). In our scientific theories, there are ideal gases, perfectly elliptical orbits, and economic consumers motivated only by profit. Everybody knows these are not intended to be real objects. Yet, it is clear that idealizations and approximations are actually needed in science in order to promote genuine explanation of many phenomena. We need to reduce the noise of the details in order to see what is important. In short, approximations and idealizations can be explanatory. But what about approximations and idealizations that involve the infinite?

Although the terms “idealization” and “approximation” are often used interchangeably, John Norton (Norton 2012) recommends paying more attention to their difference by saying that, when there is some aspect of the world, some target system, that we are trying to understand scientifically, approximations should be considered to be inexact descriptions of the target system whereas idealizations should be considered to be new systems or parts of new systems that also are approximations to the target system but that contain reference to some novel object or property. For example, elliptical orbits are approximations to actual orbits of planets, but ideal gases are idealizations because they contain novel objects such as point-sized gas particles that are part of a new system that is useful for approximating the target system of actual gases.

Philosophers of science disagree about whether all appeals to infinity can be known a priori to be mere idealizations or approximations. Our theory of the solar system justifies our belief that the Earth is orbited by a moon, not just an approximate moon. The speed of light in a vacuum really is constant, not just approximately constant. Why then should it be assumed, as it often is, that all appeals to infinity in scientific theory are approximations or idealizations? Must the infinity be an artifact of the model rather than a feature of actual physical reality?  Philosophers of science disagree on this issue. See (Mundy, 1990, p. 290).

There is an argument for believing some appeals to infinity definitely are neither approximations nor idealizations. The argument presupposes a realist rather than an antirealist understanding of science, and it begins with a description of the opponents’ position. Carl Friedrich Gauss (1777-1855) was one of the greatest mathematicians of all time. He said scientific theories involve infinities merely as approximations or idealizations and merely in order to make for easy applications of those theories, when in fact all real entities are finite. At the time, nearly everyone would have agreed with Gauss. Roger Penrose argues against Gauss’ position:

Nevertheless, as tried and tested physical theory stands today—as it has for the past 24 centuries—real numbers still form a fundamental ingredient of our understanding of the physical world. (Penrose 2004, 62)

Gauss’s position could be buttressed if there were useful alternatives to our physical theories that do not use infinities. There actually are alternative mathematical theories of analysis that do not use real numbers and do not use infinite sets and do not require the line to be dense. See (Ahmavaara 1965) for an example. Representing the majority position among scientists on this issue, Penrose says, “To my mind, a physical theory which depends fundamentally upon some absurdly enormous…number would be a far more complicated (and improbable) theory than one that is able to depend upon a simple notion of infinity” (Penrose 2005, 359). David Deutsch agrees. He says, “Versions of number theory that confined themselves to ‘small natural numbers’ would have to be so full of arbitrary qualifiers, workarounds and unanswered questions, that they would be very bad explanations until they were generalized to the case that makes sense without such ad-hoc restrictions: the infinite case.” (Deutsch 2011, pp. 118-9) And surely a successful explanation is the surest route to understanding reality.

In opposition to this position of Penrose and Deutsch, and in support of Gauss’ position, the physicist Erwin Schrödinger remarks, “The idea of a continuous range, so familiar to mathematicians in our days, is something quite exorbitant, an enormous extrapolation of what is accessible to us.” Emphasizing this point about being “accessible to us,” some metaphysicians attack the applicability of the mathematical continuum to physical reality on the grounds that a continuous human perception over time is not mathematically continuous. Wesley Salmon responds to this complaint from Schrödinger:

…The perceptual continuum and perceived becoming [that is, the evidence from our sense organs that the world changes from time to time] exhibit a structure radically different from that of the mathematical continuum. Experience does seem, as James and Whitehead emphasize, to have an atomistic character. If physical change could be understood only in terms of the structure of the perceptual continuum, then the mathematical continuum would be incapable of providing an adequate description of physical processes. In particular, if we set the epistemological requirement that physical continuity must be constructed from physical points which are explicitly definable in terms of observables, then it will be impossible to endow the physical continuum with the properties of the mathematical continuum. In our discussion…, we shall see, however, that no such rigid requirement needs to be imposed. (Salmon 1970, 20)

Salmon continues by making the point that calculus provides better explanations of physical change than explanations which accept the “rigid requirement” of understanding physical change in terms of the structure of the perceptual continuum, so he recommends that we apply Ockham’s Razor and eliminate that rigid requirement. But the issue is not settled.

d. Infinity in Cosmology

Let’s review some of the history regarding the volume of spacetime. Aristotle said the past is infinite because for any past time we can imagine an earlier one. It is difficult to make sense of his belief about the past since he means it is potentially infinite. After all, the past has an end, namely the present, so its infinity has been completed and therefore is not a potential infinity. This problem with Aristotle’s reasoning was first raised in the 13^th century by Richard Rufus of Cornwall. It was not given the attention it deserved because of the assumption for so many centuries that Aristotle couldn’t have been wrong about time, especially since his position was consistent with Christian, Jewish, and Muslim theology which implies the physical world became coherent or well-formed only a finite time ago (even if past time itself is potentially infinite). However, Aquinas argued against Aristotle’s view that the past is infinite; Aquinas’ grounds were that Holy Scripture implies God created the world (and thus time itself) a finite time ago and that Aristotle was wrong to put so much trust in what we can imagine.

Unlike time, Aristotle claimed space is finite. He said the volume of physical space is finite because it is enclosed within a finite, spherical shell of visible, fixed stars with the Earth at its center. On this topic of space not being infinite, Aristotle’s influence was authoritative to most scholars for the next eighteen hundred years.

The debate about whether the volume of space is infinite was rekindled in Renaissance Europe. The English astronomer and defender of Copernicus, Thomas Digges (1546–1595) was the first scientist to reject the ancient idea of an outer spherical shell and to declare that physical space is actually infinite in volume and filled with stars. The physicist Isaac Newton (1642–1727) at first believed the universe’s material is confined to only a finite region while it is surrounded by infinite empty space, but in 1691 he realized that if there were a finite number of stars in a finite region, then gravity would require all the stars to fall in together at some central point. To avoid this result, he later speculated that the universe contains an infinite number of stars in an infinite volume. We now know that Newton’s speculation about the stability of an infinity of stars in an infinite universe is incorrect. There would still be clumping so long as the universe did not expand. (Hawking 2001, p. 9)

Immanuel Kant (1724–1804) declared that space and time are both potentially infinite in extent because this is imposed by our own minds. Space and time are not features of “things in themselves” but are an aspect of the very form of any possible human experience, he said. We can know a priori even more about space than about time, he believed; and he declared that the geometry of space must be Euclidean. Kant’s approach to space and time as something knowable a priori went out of fashion in the early 20^th century. It was undermined in large part by the discovery of non-Euclidean geometries in the 19^th century, then by Beltrami’s and Klein’s proofs that these geometries are as logically consistent as Euclidean geometry, and finally by Einstein’s successful application to physical space of non-Euclidean geometry within his general theory of relativity.

The volume of spacetime is finite at present if we can trust the classical Big Bang theory. [But do not think of this finite space as having a boundary beyond which a traveler falls over the edge into nothingness.] Assuming space is all the places that have been created since the Big Bang, then the volume of space is definitely finite at present, though it is huge and growing ever larger over time. Assuming this expansion will never stop, it follows that the volume of spacetime is potentially infinite but not actually infinite. For more discussion of the issue of the volume of spacetime, see (Greene 2011).

Einstein’s theory of relativity implies that all physical objects must travel at less than light speed (in a vacuum). Nevertheless, by exploiting the principle of time dilation and length contraction in his special theory of relativity, the time limits on human exploration of the universe can be removed. Assuming you can travel safely at any high speed under light speed, then as your spaceship approaches light speed, your trip’s distance and travel time become infinitesimally short. In principle, you have time on your own clock to cross the Milky Way galaxy, a trip that takes light itself 100,000 years as measured on an Earth clock.

5. Infinity in Mathematics

The previous sections of this article have introduced the concepts of actual infinity and potential infinity and explored the development of calculus and set theory, but this section probes deeper into the role of infinity in mathematics. Mathematicians always have been aware of the special difficulty in dealing with the concept of infinity in a coherent manner. Intuitively, it seems reasonable that if we have two infinities of things, then we still have an infinity of them. So, we might represent this intuition mathematically by the equation 2 ∞ = 1 ∞. Dividing both sides by ∞ will prove that 2 = 1, which is a good sign we were not using infinity in a coherent manner. In recommending how to use the concept of infinity coherently, Bertrand Russell said pejoratively:

The whole difficulty of the subject lies in the necessity of thinking in an unfamiliar way, and in realising that many properties which we have thought inherent in number are in fact peculiar to finite numbers. If this is remembered, the positive theory of infinity…will not be found so difficult as it is to those who cling obstinately to the prejudices instilled by the arithmetic which is learnt in childhood. (Salmon 1970, 58)

That positive theory of infinity that Russell is talking about is set theory, and the new arithmetic is the result of Cantor’s generalizing the notions of order and of size of sets into the infinite, that is, to the infinite ordinals and infinite cardinals. These numbers are also called transfinite ordinals and transfinite cardinals. The following sections will briefly explore set theory and the role of infinity within mathematics. The main idea, though, is that the basic theories of mathematical physics are properly expressed using the differential calculus with real-number variables, and these concepts are well-defined in terms of set theory which, in turn, requires using actual infinities or transfinite infinities of various kinds.

a. Infinite Sums

In the 17^th century, when Newton and Leibniz invented calculus, they wondered what the value is of this infinite sum:

1/1 + 1/2 + 1/4 + 1/8 + ….

They believed the sum is 2. Knowing about the dangers of talking about infinity, most later mathematicians hoped to find a technique to avoid using the phrase “infinite sum.” Cauchy and Weierstrass eventually provided this technique two centuries later. They removed any mention of “infinite sum” by using the formal idea of a limit. Informally, the Cauchy-Weierstrass idea is that instead of overtly saying the infinite sum x₁ + x₂ + x₃ + … is some number S, as Newton and Leibniz were saying, one should say that the sequence converges to S just in case the numerical difference between S and any partial sum is as small as one desires, provided that partial sum occurs sufficiently far out in the sequence of partial sums. More formally it is expressed this way:

If an infinite series of real numbers is x₁ + x₂ + x₃ + …, and if the infinite sequence of its partial sums is s₁,  s₂,  s₃, …, then the series converges to S if and only if for every positive number ε there exists an integer n such that, for all integers k > n,  |s_k – S| < ε.

This technique of talking about limits was due to Cauchy in 1821 and Weierstrass in the period from 1850 to 1871. The two drawbacks to this technique are that (1) it is unintuitive and more complicated than Newton and Leibniz’s intuitive approach that did mention infinite sums, and (2) it is not needed because infinite sums were eventually legitimized by being given a set-theoretic foundation.

b. Infinitesimals and Hyperreals

There has been considerable controversy throughout history about how to understand infinitesimal objects and infinitesimal changes in the properties of objects. Intuitively, an infinitesimal object is as small as you please but not quite nothing. Infinitesimal objects and infinitesimal methods were first used by Archimedes in ancient Greece, but he did not mention them in any publication intended for the public because he did not consider his use of them to be rigorous. Infinitesimals became better known when Leibniz used them in his differential and integral calculus. The differential calculus can be considered to be a technique for treating continuous motion as being composed of an infinite number of infinitesimal steps. The calculus’ use of infinitesimals led to the so-called “golden age of nothing” in which infinitesimals were used freely in mathematics and science. During this period, Leibniz, Euler, and the Bernoullis applied the concept. Euler applied it cavalierly (although his intuition was so good that he rarely if ever made mistakes), but Leibniz and the Bernoullis were concerned with the general question of when we could, and when we could not, consider an infinitesimal to be zero. They were aware of apparent problems with these practices in large part because they had been exposed by Berkeley.

In 1734, George Berkeley attacked the concept of infinitesimal as ill-defined and incoherent because there were no definite rules for when the infinitesimal should be and shouldn’t be considered to be zero. Berkeley, like Leibniz, was thinking of infinitesimals as objects with a constant value–as genuinely infinitesimally small magnitudes–whereas Newton thought of them as variables that could arbitrarily approach zero. Either way, there were coherence problems. The scientists and results-oriented mathematicians of the golden age of nothing had no good answer to the coherence problem. As standards of rigorous reasoning increased over the centuries, mathematicians became more worried about infinitesimals. They were delighted when Cauchy in 1821 and Weierstrass in the period from 1850 to 1875 developed a way to use calculus without infinitesimals, and at this time any appeal to infinitesimals was considered illegitimate, and mathematicians soon stopped using infinitesimals.

Here is how Cauchy and Weierstrass eliminated infinitesimals with their concept of limit. Suppose we have a function f,  and we are interested in the Cartesian graph of the curve y = f(x) at some point a along the x-axis. What is the rate of change of  f at a? This is the slope of the tangent line at a, and it is called the derivative f’ at a. This derivative was defined by Leibniz to be

where h is an infinitesimal. Because of suspicions about infinitesimals, Cauchy and Weierstrass suggested replacing Leibniz’s definition of the derivative with

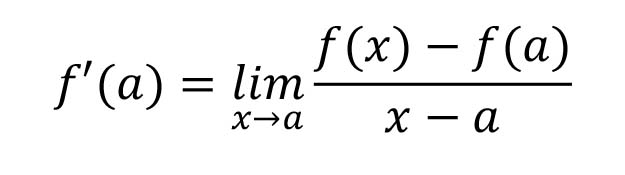
That is,  f'(a) is the limit, as x approaches a, of the above ratio. The limit idea was rigorously defined using Cauchy’s well-known epsilon and delta method. Soon after the Cauchy-Weierstrass definition of derivative was formulated, mathematicians stopped using infinitesimals.

The scientists did not follow the lead of the mathematicians. Despite the lack of a coherent theory of infinitesimals, scientists continued to reason with infinitesimals because infinitesimal methods were so much more intuitively appealing than the mathematicians’ epsilon-delta methods. Although students in calculus classes in the early 21^st century are still taught the unintuitive epsilon-delta methods, Abraham Robinson (Robinson 1966) created a rigorous alternative to standard Weierstrassian analysis by using the methods of model theory to define infinitesimals.

Here is Robinson’s idea. Think of the rational numbers in their natural order as being gappy with real numbers filling the gaps between them. Then think of the real numbers as being gappy with hyperreals filling the gaps between them. There is a cloud or region of hyperreals surrounding each real number (that is, surrounding each real number described nonstandardly). To develop these ideas more rigorously, Robinson used this simple definition of an infinitesimal:

h is infinitesimal if and only if 0 < |h| < 1/n, for every positive integer n.

|h| is the absolute value of h.

Robinson did not actually define an infinitesimal as a number on the real line. The infinitesimals were defined on a new number line, the hyperreal line, that contains within it the structure of the standard real numbers from classical analysis. In this sense, the hyperreal line is the extension of the reals to the hyperreals. The development of analysis via infinitesimals creates a nonstandard analysis with a hyperreal line and a set of hyperreal numbers that include real numbers. In this nonstandard analysis, 78+2h is a hyperreal that is infinitesimally close to the real number 78. Sums and products of infinitesimals are infinitesimal.

Because of the rigor of the extension, all the arguments for and against Cantor’s infinities apply equally to the infinitesimals. Sentences about the standardly-described reals are true if and only if they are true in this extension to the hyperreals. Nonstandard analysis allows proofs of all the classical theorems of standard analysis, but it very often provides shorter, more direct, and more elegant proofs than those that were originally proved by using standard analysis with epsilons and deltas. Objections by practicing mathematicians to infinitesimals subsided after this was appreciated. With a good definition of “infinitesimal” they could then use it to explain related concepts such as in the sentence, “That curve approaches infinitesimally close to that line.” See (Wolf 2005, chapter 7) for more about infinitesimals and hyperreals.

c. Mathematical Existence

Mathematics is apparently about mathematical objects, so it is apparently about infinitely large objects, infinitely small objects, and infinitely many objects. Mathematicians who are doing mathematics and are not being careful about ontology too easily remark that there are infinite-dimensional spaces, the continuum, continuous functions, an infinity of functions, and this or that infinite structure. Do these infinities really exist? The philosophical literature is filled with arguments pro and con and with fine points about senses of existence.

When axiomatizing geometry, Euclid said that between any two points one could choose to construct a line. Opposed to Euclid’s constructivist stance, many modern axiomatizers take a realist philosophical stance by declaring simply that there exists a line between any two points, so the line pre-exists any construction process. In mathematics, the constructivist will recognize the existence of a mathematical object only if there is at present an algorithm (that is, a step by step “mechanical” procedure operating on symbols that is finitely describable, that requires no ingenuity and that uses only finitely many steps) for constructing or finding such an object. Assertions require proofs. The constructivist believes that to justifiably assert the negation of a sentence S is to prove that the assumption of S leads to a contradiction. So, legitimate mathematical objects must be shown to be constructible in principle by some mental activity and cannot be assumed to pre-exist any such construction process nor to exist simply because their non-existence would be contradictory. A constructivist, unlike a realist, is a kind of conceptualist, one who believes that an unknowable mathematical object is impossible. Most constructivists complain that, although potential infinities can be constructed, actual infinities cannot be.

There are many different schools of constructivism. The first systematic one, and perhaps the most well-known version and most radical version, is due to L.E.J. Brouwer. He is not a finitist,  but his intuitionist school demands that all legitimate mathematics be constructible from a basis of mental processes he called “intuitions.” These intuitions might be more accurately called “clear mental procedures.” If there were no minds capable of having these intuitions, then there would be no mathematical objects just as there would be no songs without ideas in the minds of composers. Numbers are human creations. The number pi is intuitionistically legitimate because we have an algorithm for computing all its decimal digits, but the following number g is not legitimate. It is the number whose nth digit is either 0 or 1, and it is 1 if and only if there are n consecutive 7s in the decimal expansion of pi. No person yet knows how to construct the decimal digits of g. Brouwer argued that the actually infinite set of natural numbers cannot be constructed (using intuitions) and so does not exist. The best we can do is to have a rule for adding more members to a set. So, his concept of an acceptable infinity is closer to that of potential infinity than actual infinity. Hermann Weyl emphasizes the merely potential character of these infinities:

Brouwer made it clear, as I think beyond any doubt, that there is no evidence supporting the belief in the existential character of the totality of all natural numbers…. The sequence of numbers which grows beyond any stage already reached by passing to the next number, is a manifold of possibilities open towards infinity; it remains forever in the status of creation, but is not a closed realm of things existing in themselves. (Weyl is quoted in (Kleene 1967, p. 195))

It is not legitimate for platonic realists, said Brouwer, to bring all the sets into existence at once by declaring they are whatever objects satisfy all the axioms of set theory. Brouwer believed realists accept too many sets because they are too willing to accept sets merely by playing coherently with the finite symbols for them when sets instead should be tied to our experience. For Brouwer, this experience is our experience of time. He believed we should arrive at our concept of the infinite by noticing that our experience of a duration can be divided into parts and then these parts can be further divided, and so. This infinity is a potential infinity, not an actual infinity. For the intuitionist, there is no determinate, mind-independent mathematical reality that provides the facts to make mathematical sentences true or false. This metaphysical position is reflected in the principles of logic that are acceptable to an intuitionist. For the intuitionist, the sentence “For all x, x has property F” is true only if we have already proved constructively that each x has property F. And it is false only if we have proved that some x does not have property F. Otherwise, it is neither true nor false. The intuitionist does not accept the principle of excluded middle: For any sentence S, either S or the negation of S. Outraged by this intuitionist position, David Hilbert famously responded by saying, “To take the law of the excluded middle away from the mathematician would be like denying the astronomer the telescope or the boxer the use of his fists.” (quoted from Kleene 1967, p. 197) For a presentation of intuitionism with philosophical emphasis, see (Posy 2005) and (Dummett 1977).

Finitists, even those who are not constructivists, also argue that the actually infinite set of natural numbers does not exist. They say there is a finite rule for generating each numeral from the previous one, but the rule does not produce an actual infinity of either numerals or numbers. The ultrafinitist considers the classical finitist to be too liberal because finite numbers such as 2¹⁰⁰ and 2¹⁰⁰⁰ can never be accessed by a human mind in a reasonable amount of time. Only the numerals or symbols for those numbers can be coherently manipulated. One challenge to ultrafinitists is that they should explain where the cutoff point is between numbers that can be accessed and numbers that cannot be. Ultrafinitsts have risen to this challenge. The mathematician Harvey Friedman says:

I raised just this objection [about a cutoff] with the (extreme) ultrafinitist Yessenin-Volpin during a lecture of his. He asked me to be more specific. I then proceeded to start with 2¹ and asked him whether this is “real” or something to that effect. He virtually immediately said yes. Then I asked about 2², and he again said yes, but with a perceptible delay. Then 2³, and yes, but with more delay. This continued for a couple of more times, till it was obvious how he was handling this objection. Sure, he was prepared to always answer yes, but he was going to take 2¹⁰⁰ times as long to answer yes to 2¹⁰⁰ than he would to answering 2¹. There is no way that I could get very far with this. (Elwes 2010, 317)

This battle among competing philosophies of mathematics will not be explored in-depth in this article, but this section will offer a few more points about mathematical existence.

Hilbert argued that “If the arbitrarily given axioms do not contradict one another, then they are true and the things defined by the axioms exist.” But (Chihara 2008, 141) points out that Hilbert seems to be confusing truth with truth in a model. If a set of axioms is consistent, and so is its corresponding axiomatic theory, then the theory defines a class of models, and each axiom is true in any such model, but it does not follow that the axioms are really true. To give a crude, nonmathematical example, consider this set of two axioms {All horses are blue, all cows are green.}. The formal theory using these axioms is consistent and has a model, but it does not follow that either axiom is really true.

Quine objected to Hilbert’s criterion for existence as being too liberal. Quine’s argument for infinity in mathematics begins by noting that our fundamental scientific theories are our best tools for helping us understand reality and doing ontology. Mathematical theories that imply the existence of some actually infinite sets are indispensable to all these scientific theories, and their referring to these infinities cannot be paraphrased away. All this success is a good reason to believe in some actual infinite sets and to say the sentences of both the mathematical theories and the scientific theories are true or approximately true since their success would otherwise be a miracle. But, he continues, it is no miracle. See (Quine 1960 chapter 7).

Quine believed that infinite sets exist only if they are indispensable in successful applications of mathematics to science; but he believed science so far needs only the first three alephs: ℵ₀ for the integers, ℵ₁ for the set of point places in space, and ℵ₂ for the number of possible lines in space (including lines that are not continuous). The rest of Cantor’s heaven of transfinite numbers is unreal, Quine said, and the mathematics of the extra transfinite numbers is merely “recreational mathematics.” But Quine showed intellectual flexibility by saying that if he were to be convinced more transfinite sets were needed in science, then he’d change his mind about which alephs are real. To briefly summarize Quine’s position, his indispensability argument treats mathematical entities on a par with all other theoretical entities in science and says mathematical statements can be (approximately) true. Quine points out that reference to mathematical entities is vital to science, and there is no way of separating out the evidence for the mathematics from the evidence for the science. This famous indispensability argument has been attacked in many ways. Critics charge, “Quite aside from the intrinsic logical defects of set theory as a deductive theory, this is disturbing because sets are so very different from physical objects as ordinarily conceived, and because the axioms of set theory are so very far removed from any kind of empirical support or empirical testability…. Not even set theory itself can tell us how the existence of a set (e.g. a power set) is empirically manifested.” (Mundy 1990, pp. 289-90). See (Parsons 1980) for more details about Quine’s and other philosophers’ arguments about the existence of mathematical objects.

d. Zermelo-Fraenkel Set Theory

Cantor initially thought of a set as being a collection of objects that can be counted, but this notion eventually gave way to a set being a collection that has a clear membership condition. Over several decades, Cantor’s naive set theory evolved into ZF, Zermelo-Fraenkel set theory, and ZF was accepted by most mid-20^th century mathematicians as the correct tool to use for deciding which mathematical objects exist. The acceptance was based on three reasons. (1) ZF is precise and rigorous. (2) ZF is useful for defining or representing other mathematical concepts and methods. Mathematics can be modeled in set theory; it can be given a basis in set theory. (3) No inconsistency has been uncovered despite heavy usage.

Notice that one of the three reasons is not that set theory provides a foundation for mathematics in the sense of justifying the doing of mathematics or in the sense of showing its sentences are certain or necessary. Instead, set theory provides a basis for theories only in the sense that it helps to organize them, to reveal their interrelationships, and to provide a means to precisely define their concepts. The first program for providing this basis began in the late 19^th century. Peano had given an axiomatization of the natural numbers. It can be expressed in set theory using standard devices for treating natural numbers and relations and functions and so forth as being sets. (For example, zero is the empty set, and a relation is a set of ordered pairs.) Then came the arithmetization of analysis which involved using set theory to construct from the natural numbers all the negative numbers and the fractions and real numbers and complex numbers. Along with this, the principles of these numbers became sentences of set theory. In this way, the assumptions used in informal reasoning in arithmetic are explicitly stated in the formalism, and proofs in informal arithmetic can be rewritten as formal proofs so that no creativity is required for checking the correctness of the proofs. Once a mathematical theory is given a set theoretic basis in this manner, it follows that if we have any philosophical concerns about the higher level mathematical theory, those concerns will also be concerns about the lower level set theory in the basis.

In addition to Dedekind’s definition, there are other acceptable definitions of “infinite set” and “finite set” using set theory. One popular one is to define a finite set as a set onto which a one-to-one function maps the set of all natural numbers that are less than some natural number n. That finite set contains n elements. An infinite set is then defined as one that is not finite. Dedekind, himself, used another definition; he defined an infinite set as one that is not finite, but defined a finite set as any set in which there exists no one-to-one mapping of the set into a proper subset of itself. The philosopher C. S. Peirce suggested essentially the same approach as Dedekind at approximately the same time, but he received little notice from the professional community. For more discussion of the details, see (Wilder 1965, p. 66f, and Suppes 1960, p. 99n).

Set theory implies quite a bit about infinity. First, infinity in ZF has some very unsurprising features. If a set A is infinite and is the same size as set B, then B also is infinite. If A is infinite and is a subset of B, then B also is infinite. Using the axiom of choice, it follows that a set is infinite just in case for every natural number n, there is some subset whose size is n.

ZF’s axiom of infinity declares that there is at least one infinite set, a so-called inductive set containing zero and the successor of each of its members (such as {0, 1, 2, 3, …}). The power set axiom (which says every set has a power set, namely a set of all its subsets) then generates many more infinite sets of larger cardinality, a surprising result that Cantor first discovered in 1874.

In ZF, there is no set with maximum cardinality, nor a set of all sets, nor an infinitely descending sequence of sets x₀, x₁, x₂, … in which x₁ is in x₀, and x₂ is in x₁, and so forth. There is, however, an infinitely ascending sequence of sets x₀, x₁, x₂, … in which x₀ is in x₁, and x₁ is in x₂, and so forth. In ZF, a set exists if it is implied by the axioms; there is no requirement that there be some property P such that the set is the extension of P. That is, there is no requirement that the set be defined as {x| P(x)} for some property P. One especially important feature of ZF is that for any condition or property, there is only one set of objects having that property, but it cannot be assumed that for any property, there is a set of all those objects that have that property. For example, it cannot be assumed that, for the property of being a set, there is a set of all objects having that property.

In ZF, all sets are pure. A set is pure if it is empty or its members are sets, and its members’ members are sets, and so forth. In informal set theory, a set can contain cows and electrons and other non-sets.

In the early years of set theory, the terms “set” and “class” and “collection” were used interchangeably, but in von Neumann–Bernays–Gödel set theory (NBG or VBG) a set is defined to be a class that is an element of some other class. NBG is designed to have proper classes, classes that are not sets, even though they can have members which are sets. The intuitive idea is that a proper class is a collection that is too big to be a set. There can be a proper class of all sets, but neither a set of all sets nor a class of all classes. A nice feature of NBG is that a sentence in the language of ZFC is provable in NBG only if it is provable in ZFC.

Are philosophers justified in saying there is more to know about sets than is contained within ZF set theory? If V is the collection or class of all sets, do mathematicians have any access to V independently of the axioms? This is an open question that arose concerning the axiom of choice and the continuum hypothesis.

e. The Axiom of Choice and the Continuum Hypothesis

Consider whether to believe in the axiom of choice. The axiom of choice is the assertion that, given any collection of non-empty and non-overlapping sets, there exists a ‘choice set’ which is composed of one element chosen from each set in the collection. However, the axiom does not say how to do the choosing. For some sets, there might not be a precise rule of choice. If the collection is infinite and its sets are not well-ordered in any way that has been specified, then there is, in general, no way to define the choice set. The axiom is implicitly used throughout the field of mathematics, and several important theorems cannot be proved without it. Mathematical Platonists tend to like the axiom, but those who want explicit definitions or constructions for sets do not like it. Nor do others who note that mathematics’ most unintuitive theorem, the Banach-Tarski Theorem, requires the axiom of choice. The dispute can get quite intense with advocates of the axiom of choice saying that their opponents are throwing out invaluable mathematics, while these opponents consider themselves to be removing tainted mathematics. See (Wagon 1985) for more on the Banach-Tarski Theorem; see (Wolf 2005, pp. 226-8) for more discussion of which theorems require the axiom.

A set is always smaller than its power set. How much bigger is the power set? Cantor’s controversial continuum hypothesis says that the cardinality of the power set of ℵ₀ is ℵ₁, the next larger cardinal number, and not some higher cardinal. The generalized continuum hypothesis is more general; it says that, given an infinite set of any cardinality, the cardinality of its power set is the next larger cardinal and not some even higher cardinal. Cantor believed the continuum hypothesis, but he was frustrated that he could not prove it. The philosophical issue is whether we should alter the axioms to enable the hypotheses to be proved.

If ZF is formalized as a first-order theory of deductive logic, then both Cantor’s generalized continuum hypothesis and the axiom of choice are consistent with Zermelo Frankel set theory but cannot be proved or disproved from them, assuming that ZF is not inconsistent. In this sense, both the continuum hypothesis and the axiom of choice are independent of ZF. Gödel in 1940 and Cohen in 1964 contributed to the proof of this independence result.

So, how do we decide whether to believe the axiom of choice and continuum hypothesis, and how do we decide whether to add them to the principles of ZF or any other set theory? Most mathematicians do believe the axiom of choice is true, but there is more uncertainty about the continuum hypothesis. The independence does not rule out our someday finding a convincing argument that the hypothesis is true or a convincing argument that it is false, but the argument will need more premises than just the principles of ZF. At this point, the philosophers of mathematics divide into two camps. The realists, who think there is a unique universe of sets to be discovered, believe that if ZF does not fix the truth values of the continuum hypothesis and the axiom of choice, then this is a defect within ZF and we need to explore our intuitions about infinity in order to uncover a missing axiom or two for ZF that will settle the truth values. These persons prefer to think that there is a single system of mathematics to which set theory is providing a foundation, but they would prefer not simply to add the continuum hypothesis itself as an axiom because the hope is to make the axioms “readily believable,” yet it is not clear enough that the axiom itself is readily believable. The second camp of philosophers of mathematics disagree and say the concept of infinite set is so vague that we simply do not have any intuitions that will or should settle the truth values. According to this second camp, there are set theories with and without axioms that fix the truth values of the axiom of choice and the continuum hypothesis, and set theory should no more be a unique theory of sets than Euclidean geometry should be the unique theory of geometry.

Believing that ZFC’s infinities are merely the above-surface part of the great iceberg of infinite sets, many set theorists are actively exploring new axioms that imply the existence of sets that could not be proved to exist within ZFC. So far there is no agreement among researchers about the acceptability of any of the new axioms. See (Wolf 2005, pp. 226-8) and (Rucker 1982, pp. 252-3) for more discussion of the search for these new axioms.

6. Infinity in Deductive Logic

The infinite appears in many interesting ways in formal deductive logic, and this section presents an introduction to a few of those ways. Among all the various kinds of formal deductive logics, first-order logic (the usual predicate logic) stands out as especially important, in part because of the accuracy and detail with which it can mirror mathematical deductions. First-order logic also stands out because it is the strongest logic that has proofs for every one of its infinitely numerous logically true sentences, and that is compact in the sense that if an infinite set of its sentences is inconsistent, then so is some finite subset. But first-order logic has expressive limitations:

[M]any central concepts—such as finitude, countability, minimal closure, wellfoundedness, and well-order, cannot be captured in a first-order language. The Lowenheim-Skolem theorems entail that no infinite structure can be characterized up to isomorphism in a first-order language. …The aforementioned mathematical notions that lack first-order characterizations all have adequate characterizations in second-order languages.
Stewart Shapiro, Handbook of Philosophical Logic, p. 131.

Let’s be clearer about just what first-order logic is. To answer this and other questions, it is helpful to introduce some technical terminology. Here is a chart of what is ahead:

	First-order language	First-order theory	First-order formal system	First-order logic
Definition	Formal language with quantifiers over objects but not over sets of objects.	A set of sentences expressed in a first-order language.	First-order theory plus its method for building proofs.	First-order language with its method for building proofs.

A first-order theory is a set of sentences expressed in a first-order language (which will be defined below). A first-order formal system is a first-order theory plus its deductive structure (method of building proofs). Intuitively and informally, any formal system is a system of symbols that are manipulated by the logician in game-like fashion for the purpose of more deeply understanding the properties of the structure that is represented by the formal system. The symbols denote elements or features of the structure the formal system is being used to represent.

The term “first-order logic” is ambiguous. It can mean a first-order language with its deductive structure, or a first-order language with its semantics, or the academic discipline that studies first-order languages and theories.

Classical first-order logic is classical predicate logic with its core of classical propositional logic. This logic is distinguished by its satisfying certain classically-accepted assumptions: that it has only two truth values (some non-classical logics have an infinite number of truth-values), every sentence (that is, proposition) gets exactly one of the two truth values; no sentence can contain an infinite number of symbols; a valid deduction cannot be made from true sentences to a false one; deductions cannot be infinitely long; the domain of an interpretation cannot be empty but can have any infinite cardinality; an individual constant (name) must name something in the domain; and so forth.

A formal language specifies the language’s vocabulary symbols and its syntax, primarily what counts as being a term or name and what are its well-formed formulas (wffs). A first-order language is a formal language whose symbols are the quantifiers (for example, ∃), connectives (↔), individual constants (a), individual variables (x), predicates or relations (R), and perhaps functions (f) and equality (=). It has a denumerable list of variables. (A set is denumerable or countably infinite if it has size ℵ₀.) A first-order language has a countably finite or countably infinite number of predicate symbols and function symbols, but not a zero number of both. First-order languages differ from each other only in their predicate symbols or function symbols or constants symbols or in having or not having the equality symbol. See (Wolf 2005, p. 23) for more details. There are denumerably many terms, formulas, and sentences. Also, because there are uncountably many real numbers, a theory of real numbers in a first-order language does not have enough names for all the real numbers.

To carry out proofs or deductions in a first-order language, the language needs to be given a deductive structure. There are several different ways to do this (via axioms, natural deduction, sequent calculus), but the ways are all independent of which first-order language is being used, and they all require specifying rules such as modus ponens for how to deduce wffs from finitely many previous wffs in the deduction.

To give some semantics or meaning to its symbols, the first-order language needs a definition of valuation and of truth in a valuation and of validity of an argument. In a propositional logic, the valuation assigns to each sentence letter its own single truth value; in predicate logic each term is given its own denotation (its extension), and each predicate is given a set of objects (its extension) in the domain that satisfy the predicate. The valuation rules then determine the truth values of all the wffs. The valuation’s domain is a set containing all the objects that the terms might denote and that the variables range over. The domain may be of any finite or transfinite size, but the variables can range only over objects in this domain, not over sets of those objects.

Tarski, who was influential in giving an appropriate, rigorous definition to first-ordr language, was always bothered by the tension between his nominalist view of language as the product of human activity, which is finite, and his view that intellectual progress in logic and mathematics requires treating a formal language as having infinite features such as an infinity of sentences. This article does not explore how this tension can be eased, or whether it should be.

Because a first-order language cannot successfully express sentences that generalize over sets (or properties or classes or relations) of the objects in the domain, it cannot, for example, adequately express Leibniz’s Law that, “If objects a and b are identical, then they have the same properties.” A second-order language can do this. A language is second-order if in addition to quantifiers on variables that range over objects in the domain it also has quantifiers (such as the universal quantifier ∀P) on a second kind of variable P that ranges over properties (or classes or relations) of these objects. Here is one way to express Leibniz’s Law in second-order logic:

(a = b) –> ∀P(Pa ↔ Pb)

P is called a predicate variable or property variable. Every valid deduction in first-order logic is also valid in second-order logic. A language is third-order if it has quantifiers on variables that range over properties of properties of objects (or over sets of sets of objects), and so forth. A language is called higher-order if its order is second-order or higher.

The definition of first-order theory given earlier in this section was that it is any set of wffs in a first-order language. A more ordinary definition adds that it is closed under deduction. This additional requirement implies that every deductive consequence of some sentences of the theory also is in the theory. Since the consequences are countably infinite, all ordinary first-order theories are countably infinite.

If the language is not explicitly mentioned for a first-order theory, then it is generally assumed that the language is the smallest first-order language that contains all the sentences of the theory. Valuations of the language in which all the sentences of the theory are true are said to be models of the theory.

If the theory is axiomatized, then in addition to the logical axioms there are proper axioms (also called non-logical axioms); these axioms are specific to the theory (and so usually do not hold in other first-order theories). For example, Peano’s axioms when expressed in a first-order language are proper axioms for the formal theory of arithmetic, but they aren’t logical axioms or logical truths. See (Wolf, 2005, pp. 32-3) for specific proper axioms of Peano Arithmetic and for proofs of some of its important theorems.

Besides the above problem about Leibniz’s Law, there is a related problem about infinity that occurs when Peano Arithmetic is expressed as a first-order theory. Gödel’s First Incompleteness Theorem proves that there are some bizarre truths which are independent of first-order Peano Arithmetic (PA), and so cannot be deduced within PA. None of these truths so far are known to lie in mainstream mathematics. But they might. And there is another reason to worry about the limitations of PA. Because the set of sentences of PA is only countable, whereas there are uncountably many sets of numbers in informal arithmetic, it might be that PA is inadequate for expressing and proving some important theorems about sets of numbers. See (Wolf 2005, pp. 33-4, 225).

It seems that all the important theorems of arithmetic and the rest of mathematics can be expressed and proved in another first-order theory, Zermelo-Fraenkel set theory with the axiom of choice (ZFC). Unlike first-order Peano Arithmetic, ZFC needs only a very simple first-order language that surprisingly has no undefined predicate symbol, equality symbol, relation symbol, or function symbol, other than a single two-place binary relation symbol intended to represent set membership. The domain is intended to be composed only of sets but since mathematical objects can be defined to be sets, the domain contains these mathematical objects.

a. Finite and Infinite Axiomatizability

In the process of axiomatizing a theory, any sentence of the theory can be called an axiom. When axiomatizing a theory, there is no problem with having an infinite number of axioms so long as the set of axioms is decidable, that is, so long as there is a finitely long computation or mechanical procedure for deciding, for any sentence, whether it is an axiom.

Logicians are curious as to which formal theories can be finitely axiomatized in a given formal system and which can only be infinitely axiomatized. Group theory is finitely axiomatizable in classical first-order logic, but Peano Arithmetic and ZFC are not. Peano Arithmetic is not finitely axiomatizable because it requires an axiom scheme for induction. An axiom scheme is a countably infinite number of axioms of similar form, and an axiom scheme for induction would be an infinite number of axioms of the form (expressed here informally): “If property P of natural numbers holds for zero, and also holds for n+1 whenever it holds for natural number n, then P holds for all natural numbers.” There needs to be a separate axiom for every property P, but there is a countably infinite number of these properties expressible in a first-order language of elementary arithmetic.

Assuming ZF is consistent, ZFC is not finitely axiomatizable in first-order logic, as Richard Montague discovered. Nevertheless, ZFC is a subset of von Neumann–Bernays–Gödel (NBG) set theory, and the latter is finitely axiomatizable, as Paul Bernays discovered. The first-order theory of Euclidean geometry is not finitely axiomatizable, and the second-order logic used in (Field 1980) to reconstruct mathematical physics without quantifying over numbers also is not finitely axiomatizable. See (Mendelson 1997) for more discussion of finite axiomatizability.

b. Infinitely Long Formulas

An infinitary logic is a logic that makes one of classical logic’s necessarily finite features be infinite. In the languages of classical first-order logic, every formula is required to be only finitely long, but an infinitary logic might relax this. The original, intuitive idea behind requiring finitely long sentences in classical logic was that logic should reflect the finitude of the human mind. But with increasing opposition to psychologism in logic, that is, to making logic somehow dependent on human psychology, researchers began to ignore the finitude restrictions. Löwenheim in about 1915 was perhaps the pioneer here. In 1957, Alfred Tarski and Dana Scott explored permitting the operations of conjunction and disjunction to link infinitely many formulas into an infinitely long formula. Tarski also suggested allowing formulas to have a sequence of quantifiers of any transfinite length. William Hanf proved in 1964 that, unlike classical logics, these infinitary logics fail to be compact. See (Barwise 1975) for more discussion of these developments.

c. Infinitely Long Proofs

Classical formal logic requires any proof to contain a finite number of steps. In the mid-20^th century with the disappearance of psychologism in logic, researchers began to investigate logics with infinitely long proofs as an aid to simplifying consistency proofs. See (Barwise 1975).

d. Infinitely Many Truth Values

One reason for permitting an infinite number of truth-values is to represent the idea that truth is a matter of degree. The intuitive idea is that, say, depending on the temperature, the truth of “This cup of coffee is warm” might be definitely true, less true, even less true, and so forth.

One of the simplest infinite-valued semantics uses a continuum of truth values. Its valuations assign to each basic sentence (a formal sentence that contains no connectives or quantifiers) a truth value that is a specific number in the closed interval of real numbers from 0 to 1. The truth-value of the vague sentence “This water is warm” is understood to be definitely true if it has the truth value 1 and definitely false if it has the truth value 0. To sentences having main connectives, the valuation assigns to the negation ~P of any sentence P the truth value of one minus the truth value assigned to P. It assigns to the conjunction P & Q the minimum of the truth values of P and of Q. It assigns to the disjunction P v Q the maximum of the truth values of P and of Q, and so forth.

One advantage of using an infinite-valued semantics is that by permitting modus ponens to produce a conclusion that is slightly less true than either premise, we can create a solution to the paradox of the heap, the sorites paradox. One disadvantage is that there is no well-motivated choice for the specific real number that is the truth value of a vague statement. What is the truth value appropriate to “This water is warm” when the temperature is 100 degrees Fahrenheit and you are interested in cooking pasta in it? Is the truth value 0.635? This latter problem of assigning truth values to specific sentences without being arbitrary has led to the development of fuzzy logics in place of the simpler infinite-valued semantics we have been considering. Lofti Zadeh suggested that instead of vague sentences having any of a continuum of precise truth values we should make the continuum of truth values themselves imprecise. His suggestion was to assign a sentence a truth value that is a fuzzy set of numerical values, a set for which membership is a matter of degree. For more details, see (Nolt 1997, pp. 420-7).

e. Infinite Models

A countable language is a language with countably many symbols. The Löwenhim Skolem Theorem says:

If a first-order theory in a countable language has an infinite model, then it has a countably infinite model.

This is a surprising result about infinity. Would you want your theory of real numbers to have a countable model? Strictly speaking, it is a puzzle and not a paradox because the property of being countably infinite is a property it has when viewed from outside the object language not within it. The theorem does not imply first-order theories of real numbers must have no more real numbers than there are natural numbers.

The Löwenhim-Skolem Theorem can be extended to say that if a theory in a countable language has a model of some infinite size, then it also has models of any infinite size. This is a limitation on first-order theories; they do not permit having a categorical theory of an infinite structure. A formal theory is said to be categorical if any two models satisfying the theory are isomorphic. The two models are isomorphic if they have the same structure, and they can’t be isomorphic if they have different sizes. So, if you create a first-order theory intended to describe a single infinite structure of a certain size, the theory will end up having, for any infinite size, a model of that size. This frustrates the hopes of anyone who would like to have a first-order theory of arithmetic that has models only of size ℵ₀, and to have a first-order theory of real numbers that has models only of size 2^ℵ₀. See (Enderton 1972, pp. 142-3) for more discussion of this limitation.

Because of this limitation, many logicians have turned to second-order logics. There are second-order categorical theories for the natural numbers and for the real numbers. Unfortunately, there is no sound and complete deductive structure for any second-order logic having a decidable set of axioms; this is a major negative feature of second-order logics.

To illustrate one more surprise regarding infinity in formal logic, notice that the quantifiers are defined in terms of their domain, the domain of discourse. In a first-order set theory, the expression ∃xPx says there exists some set x in the infinite domain of all the sets such that x has property P. Unfortunately, in ZF there is no set of all sets to serve as this domain. So, it is oddly unclear what the expression ∃xPx means when we intend to use it to speak about sets.

f. Infinity and Truth

According to Alfred Tarski’s Undefinability Theorem, in an arbitrary first-order language, a global truth predicate is not definable. A global truth predicate is a predicate that is satisfied by all and only the names (via, say, Gödel numbering) of all the true sentences of the formal language. According to Tarski, since no single language has a global truth predicate, the best approach to expressing truth formally within the language is to expand the language into an infinite hierarchy of languages, with each higher language (the metalanguage) containing a truth predicate that can apply to all and only the true sentences of languages lower in the hierarchy. This process is iterated into the transfinite to obtain Tarski’s hierarchy of metalanguages. Some philosophers have suggested that this infinite hierarchy is implicit within natural languages such as English, but other philosophers, including Tarski himself, believe an informal language does not contain within it a formal language.

To handle the concept of truth formally, Saul Kripke rejects the infinite hierarchy of metalanguages in favor of an infinite hierarchy of interpretations (that is, valuations) of a single language, such as a first-order predicate calculus, with enough apparatus to discuss its own syntax. The language’s intended truth predicate T is the only basic (atomic) predicate that is ever partially-interpreted at any stage of the hierarchy. At the first step in the hierarchy, all predicates but the single one-place predicate T(x) are interpreted. T(x) is completely uninterpreted at this level. As we go up the hierarchy, the interpretation of the other basic predicates are unchanged, but T is satisfied by the names of sentences that were true at lower levels. For example, at the second level, T is satisfied by the name of the sentence ∀x(Fx v ~Fx). At each step in the hierarchy, more sentences get truth values, but any sentence that has a truth value at one level has that same truth value at all higher levels. T almost becomes a global truth predicate when the inductive interpretation-building reaches the first so-called fixed point level. At this countably infinite level, although T is a truth predicate for all those sentences having one of the two classical truth values, the predicate is not quite satisfied by the names of every true sentence because it is not satisfied by the names of some of the true sentences containing T. At this fixed point level, the Liar sentence (of the Liar Paradox) is still neither true nor false. For this reason, the Liar sentence is said to fall into a “truth gap” in Kripke’s theory of truth. See (Kripke, 1975).

(Yablo 1993) produced a semantic paradox somewhat like the Liar Paradox. Yablo claimed there is no way to coherently assign a truth value to any of the sentences in the countably infinite sequence of sentences of the form, “None of the subsequent sentences are true.” Ask yourself whether the first sentence in the sequence could be true. Notice that no sentence overtly refers to itself. There is controversy in the literature about whether the paradox actually contains a hidden appeal to self-reference, and there has been some investigation of the parallel paradox in which “true” is replaced by “provable.” See (Beall 2001).

7. Conclusion

There are many aspects of the infinite that this article does not cover. Here are some of them: an upper limit on the amount of information in the universe, renormalization in quantum field theory, supertasks and infinity machines, categorematic and syncategorematic uses of the word “infinity,” mereology, ordinal and cardinal arithmetic in ZF, the various non-ZF set theories, non-standard solutions to Zeno’s Paradoxes, Cantor’s arguments for the Absolute, Kant’s views on the infinite, quantifiers that assert the existence of uncountably many objects, and the detailed arguments for and against constructivism, intuitionism, and finitism. For more discussion of these latter three programs, see (Maddy 1992).

8. References and Further Reading

• Ahmavaara, Y. (1965). “The Structure of Space and the Formalism of Relativistic Quantum Theory,” Journal of Mathematical Physics, 6, 87-93.
  • Uses finite arithmetic in mathematical physics, and argues that this is the correct arithmetic for science.
• Barrow, John D. (2005). The Infinite Book: A Short Guide to the Boundless, Timeless and Endless. Pantheon Books, New York.
  • An informal and easy-to-understand survey of the infinite in philosophy, theology, science, and mathematics. Says which Western philosopher throughout the centuries said what about infinity.
• Barwise, Jon. (1975) “Infinitary Logics,” in Modern Logic: A Survey, E. Agazzi (ed.), Reidel, Dordrecht, pp. 93-112.
  • An introduction to infinitary logics that emphasizes historical development.
• Beall, J.C. (2001). “Is Yablo’s Paradox Non-Circular?” Analysis 61, no. 3, pp. 176-87.
  • Discusses the controversy over whether the Yablo Paradox is or isn’t indirectly circular.
• Cantor, Georg. (1887). “Über die verschiedenen Ansichten in Bezug auf die actualunendlichen Zahlen.” Bihang till Kongl. Svenska Vetenskaps-Akademien Handlingar , Bd. 11 (1886-7), article 19. P. A. Norstedt & Sôner: Stockholm.
  • A very early description of set theory and its relationship to old ideas about infinity.
• Chihara, Charles. (1973). Ontology and the Vicious-Circle Principle. Ithaca: Cornell University Press.
  • Pages 63-65 give Chihara’s reasons for why the Gödel-Cohen independence results are evidence against mathematical Platonism.
• Chihara, Charles. (2008). “The Existence of Mathematical Objects,” in Proof & Other Dilemmas: Mathematics and Philosophy, Bonnie Gold & Roger A. Simons, eds., The Mathematical Association of America.
  • In chapter 7, Chihara provides a fine survey of the ontological issues in mathematics.
• Deutsch, David. (2011). The Beginning of Infinity: Explanations that Transform the World. Penguin Books, New York City.
  • Emphasizes the importance of successful explanation in understanding the world, and provides new ideas on the nature and evolution of our knowledge.
• Descartes, René. (1641). Meditations on First Philosophy.
  • The third meditation says, “But these properties [of God] are so great and excellent, that the more attentively I consider them the less I feel persuaded that the idea I have of them owes its origin to myself alone. And thus it is absolutely necessary to conclude, from all that I have before said, that God exists….”
• Dummett, Michael. (1977). Elements of Intuitionism. Oxford University Press, Oxford.
  • A philosophically rich presentation of intuitionism in logic and mathematics.
• Elwes, Richard. (2010). Mathematics 1001: Absolutely Everything That Matters About Mathematics in 1001 Bite-Sized Explanations, Firefly Books, Richmond Hill, Ontario.
  • Contains the quoted debate between Harvey Friedman and a leading ultrafinitist.
• Enderton, Herbert B. (1972). A Mathematical Introduction to Logic. Academic Press: New York.
  • An introduction to deductive logic that presupposes the mathematical sophistication of an advanced undergraduate mathematics major. The corollary proved on p. 142 says that if a theory in a countable language has a model of some infinite size, then it also has models of any infinite size.
• Feferman, Anita Burdman, and Solomon. (2004) Alfred Tarski: Life and Logic, Cambridge University Press, New York.
  • A biography of Alfred Tarski, the 20^th century Polish and American logician.
• Field, Hartry. (1980). Science Without Numbers: A Defense of Nominalism. Princeton: Princeton University Press.
  • Field’s program is to oppose the Quine-Putnam Indispensability argument which apparently implies that mathematical physics requires the existence of mathematical objects such as numbers and sets. Field tries to reformulate scientific theories so, when they are formalized in second-order logic, their quantifiers do not range over abstract mathematical entities. Field’s theory uses quantifiers that range over spacetime points. However, because it uses a second-order logic, the theory is also committed to quantifiers that range over sets of spacetime points, and sets are normally considered to be mathematical objects.
• Gödel, Kurt. (1947/1983). “What is Cantor’s Continuum Problem?” American Mathematical Monthly 54, 515-525. Revised and reprinted in Philosophy of Mathematics: Selected Readings, Paul Benacerraf and Hilary Putnam (eds.), Prentice-Hall, Inc. Englewood Cliffs, 1964.
  • Gödel argues that the failure of ZF to provide a truth value for Cantor’s continuum hypothesis implies a failure of ZF to correctly describe the Platonic world of sets.
• Greene, Brian. (2004). The Fabric of Reality. Random House, Inc., New York.
  • Promotes the virtues of string theory.
• Greene, Brian (1999). The Elegant Universe. Vintage Books, New York.
  • The quantum field theory called quantum electrodynamics (QED) is discussed on pp. 121-2.
• Greene, Brian. (2011). The Hidden Reality: Parallel Universes and the Deep Laws of the Cosmos. Vintage Books, New York.
  • A popular survey of cosmology with an emphasis on string theory.
• Hawking, Stephen. (2001). The Illustrated A Brief History of Time: Updated and Expanded Edition. Bantam Dell. New York.
  • Chapter 4 of Brief History contains an elementary and non-mathematical introduction to quantum mechanics and Heisenberg’s uncertainty principle.
• Hilbert, David. (1925). “On the Infinite,” in Philosophy of Mathematics: Selected Readings, Paul Benacerraf and Hilary Putnam (eds.), Prentice-Hall, Inc. Englewood Cliffs, 1964. 134-151.
  • Hilbert promotes what is now called the Hilbert Program for solving the problem of the infinite by requiring a finite basis for all acceptable assertions about the infinite.
• Kleene, (1967). Mathematical Logic. John Wiley & Sons: New York.
  • An advanced textbook in mathematical logic.
• Kripke, Saul. (1975). “Outline of a Theory of Truth,” Journal of Philosophy 72, pp. 690–716.
  • Describes how to create a truth predicate within a formal language that avoids assigning a truth value to the Liar Sentence.
• Leibniz, Gottfried. (1702). “Letter to Varignon, with a note on the ‘Justification of the Infinitesimal Calculus by that of Ordinary Algebra,'” pp. 542-6. In Leibniz Philosophical Papers and Letters. translated by Leroy E. Loemkr (ed.). D. Reidel Publishing Company, Dordrecht, 1969.
  • Leibniz defends the actual infinite in calculus.
• Levinas, Emmanuel. (1961). Totalité et Infini. The Hague: Martinus Nijhoff.
  • In Totality and Infinity, the Continental philosopher Levinas describes infinity in terms of the possibilities a person confronts upon encountering other conscious beings.
• Maddy, Penelope. (1992). Realism in Mathematics. Oxford: Oxford University Press.
  • A discussion of the varieties of realism in mathematics and the defenses that have been, and could be, offered for them. The book is an extended argument for realism about mathematical objects. She offers a set-theoretic monism in which all physical objects are sets.
• Maor, E. (1991). To Infinity and Beyond: A Cultural History of the Infinite. Princeton: Princeton University Press.
  • A survey of many of the issues discussed in this encyclopedia article.
• Mendelson, Elliolt. (1997). An Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall.
  • Pp. 225–86 discuss NBG set theory.
• Mill, John Stuart. (1843). A System of Logic: Ratiocinative and Inductive. Reprinted in J. M. Robson, ed., Collected Works, volumes 7 and 8. Toronto: University of Toronto Press, 1973.
  • Mill argues for empiricism and against accepting the references of theoretical terms in scientific theories if the terms can be justified only by the explanatory success of those theories.
• Moore, A. W. (2001). The Infinite. Second edition, Routledge, New York.
  • A popular survey of the infinite in metaphysics, mathematics, and science.
• Mundy, Brent. (1990). “Mathematical Physics and Elementary Logic,” Proceedings of the Biennial Meeting of the Philosophy of Science Association. Vol. 1990, Volume 1. Contributed Papers (1990), pp. 289-301.
  • Discusses the relationships among set theory, logic and physics.
• Nolt, John. Logics. (1997). Wadsworth Publishing Company, Belmont, California.
  • An undergraduate logic textbook containing in later chapters a brief introduction to non-standard logics such as those with infinite-valued semantics.
• Norton, John. (2012). “Approximation and Idealization: Why the Difference Matters,” Philosophy of Science, 79, pp. 207-232.
  • Recommends being careful about the distinction between approximation and idealization in science.
• Owen, H. P. (1967). “Infinity in Theology and Metaphysics.” In Paul Edwards (Ed.) The Encyclopedia of Philosophy, volume 4, pp. 190-3.
  • This survey of the topic is still reliable.
• Parsons, Charles. (1980). “Quine on the Philosophy of Mathematics.” In L. Hahn and P. Schilpp (Eds.) The Philosophy of W. V. Quine, pp. 396-403. La Salle IL: Open Court.
  • Argues against Quine’s position that whether a mathematical entity exists depends on the indispensability of the mathematical term denoting that entity in a true scientific theory.
• Penrose, Roger. (2005). The Road to Reality: A Complete Guide to the Laws of the Universe. New York: Alfred A. Knopf.
  • A fascinating book about the relationship between mathematics and physics. Many of its chapters assume sophistication in advanced mathematics.
• Posy, Carl. (2005). “Intuitionism and Philosophy.” In Stewart Shapiro. Ed. (2005). The Oxford Handbook of Philosophy of Mathematics and Logic. Oxford: Oxford University Press.
  • The history of the intuitionism of Brouwer, Heyting and Dummett. Pages 330-1 explains how Brouwer uses choice sequences to develop “even the infinity needed to produce a continuum” non-empirically.
• Quine, W. V. (1960). Word and Object. Cambridge: MIT Press.
  • Chapter 7 introduces Quine’s viewpoint that set-theoretic objects exist because they are needed on the basis of our best scientific theories.
• Quine, W. V. (1986). The Philosophy of W. V. Quine. Editors: Lewis Edwin Hahn and Paul Arthur Schilpp, Open Court, LaSalle, Illinois.
  • Contains the quotation saying infinite sets exist only insofar as they are needed for scientific theory.
• Robinson, Abraham. (1966). Non-Standard Analysis. Princeton Univ. Press, Princeton.
  • Robinson’s original theory of the infinitesimal and its use in real analysis to replace the Cauchy-Weierstrass methods that use epsilons and deltas.
• Rucker, Rudy. (1982). Infinity and the Mind: The Science and Philosophy of the Infinite. Birkhäuser: Boston.
  • A survey of set theory with much speculation about its metaphysical implications.
• Russell, Bertrand. (1914). Our Knowledge of the External World as a Field for Scientific Method in Philosophy. Open Court Publishing Co.: Chicago.
  • Russell champions the use of contemporary real analysis and physics in resolving Zeno’s paradoxes. Chapter 6 is “The Problem of Infinity Considered Historically,” and that chapter is reproduced in (Salmon, 1970).
• Salmon, Wesley, ed. (1970). Zeno’s Paradoxes. The Bobbs-Merrill Company, Inc., Indianapolis.
  • A collection of the important articles on Zeno’s Paradoxes plus a helpful and easy-to-read preface providing an overview of the issues.
• Shapiro, Stewart. (2001). “Systems between First-Order and Second-Order Logics,” in D. M. Gabbay and F. Guenthner (eds.),
  Handbook of Philosophical Logic, 2nd Edition, Volume I,
  Kluwer Academic Publishers, pp. 131-187.
  • Surveys first-order logics, second-order logics, and systems between them.
• Smullyan, Raymond. (1967). “Continuum Problem,” in Paul Edwards (ed.), The Encyclopedia of Philosophy, Macmillan Publishing Co. & The Free Press: New York.
  • Discusses the variety of philosophical reactions to the discovery of the independence of the continuum hypotheses from ZF set theory.
• Suppes, Patrick. (1960). Axiomatic Set Theory. D. Van Nostrand Company, Inc.: Princeton.
  • An undergraduate-level introduction to set theory.
• Tarski, Alfred. (1924). “Sur les Ensembles Finis,” Fundamenta Mathematicae, Vol. 6, pp. 45-95.
  • Surveys and evaluates alternative definitions of finitude and infinitude proposed by Zermelo, Russell, Sierpinski, Kuratowski, Tarski, and others.
• Wagon, Stan. (1985). The Banach-Tarski Paradox. Cambridge University Press: Cambridge.
  • The unintuitive Banach-Tarski Theorem says a solid sphere can be decomposed into a finite number of parts and then reassembled into two solid spheres of the same radius as the original sphere. Unfortunately, you cannot double your sphere of solid gold this way.
• Wilder, Raymond L. (1965) Introduction to the Foundations of Mathematics, 2^nd ed., John Wiley & Sons, Inc.: New York.
  • An undergraduate-level introduction to the foundation of mathematics.
• Wolf, Robert S. (2005). A Tour through Mathematical Logic. The Mathematical Association of America: Washington, D.C.
  • Chapters 2 and 6 describe set theory and its historical development. Both the history of the infinitesimal and the development of Robinson’s nonstandard model of analysis are described clearly on pages 280-316.
• Yablo, Stephen. (1993). “Paradox without Self-Reference.” Analysis 53: 251-52.
  • Yablo presents a Liar-like paradox involving an infinite sequence of sentences that, the author claims, is “not in any way circular,” unlike with the traditional Liar Paradox.

Author Information

Bradley Dowden
Email: dowden@csus.edu
California State University Sacramento
U. S. A.