Classification

One of the main topics of scientific research is classification. Classification is the operation of distributing objects into classes or groups—which are, in general, less numerous than them. It has a long history that has developed during four periods: (1) Antiquity, where its lineaments may be found in the writings of Plato and Aristotle; (2) The Classical Age, with natural scientists from Linnaeus to Lavoisier; (3) The 19th century, with the growth of chemistry and information science; and (4) the 20th century, with the arrival of mathematical models and computer science. Since that time, and from an extensional viewpoint, mathematics, specifically, the theory of orders and the theory of graphs or hypergraphs, has facilitated the precise study of strong and weak forms of order in the world, and the computation of all the possible partitions, chains of partitions, covers, hypergraphs or systems of classes that we can construct on a domain. With the development of computer science, Artificial Intelligence, and new kinds of languages such as oriented-objected languages, an intensional approach has completed the previous one. Ancient discussions between Aristotle and Plato, Ramus and Pascal, Jevons and Joseph found some kind of revival via object-oriented modeling and programming, most of objected oriented languages being concerned with hierarchies, or partial orders: these structures reflect in fact the relations between classes in those languages, which generally admit single or multiple inheritance. In spite of these advances, most of classifications are still based on the evaluation of resemblances between objects that constitute the empirical data. This one is almost always computed by the means of some notion of distance and of some algorithms of aggregation of classes. So all these classifications remain, for technical and epistemological reasons that are detailed below, very unstable ones. A real algebra of classifications, which could explain their properties and the relations existing between them, is lacking. Though the aim of a general theory of classifications is surely a wishful thought, some recent conjecture gives the hope that the existence of a metaclassification (or classification of all classification schemes) is possible.

General Introduction: Classification Problems
A Brief History of Classifications
The Problem of Information Storage and Retrieval
Ranganathan and the PMEST Scheme
Order and Mathematical Models
1. Extensional Structures
2. A Glance at an Intensional Approach
The Idea of a General Theory of Classifications
References and Further Readings

1. General Introduction: Classification Problems

Classification problems are one of the basic topics of scientific research. For example, mathematics, physics, natural sciences, social sciences and, of course, library and information sciences all make use of taxonomies. Classification is a very useful tool for ordering and organization. It has increased knowledge and helped to facilitate information retrieval.

Roughly speaking, ‘classification’ is the operation consisting of sharing, distributing or allocating objects in classes or groups which are, in general, less numerous than them. Commonly, classifications are defined on finite sets. However, if the objects are, for example, mathematical structures there can be infinite classifications. In this case, the previous requirement, of course, must be weakened: we may only want the (infinite) cardinal of the classification to be less than or equal to the (infinite) cardinal of the set of objects to be classified. What we call ‘classification’ is also the result of this operation. We want, as much as it is possible, for this result be constant, namely, that the classification itself remains stable for a little transformation of data (of course, the sense of this requirement will have to become clearer). Various situations may happen: the classes may intersect or not, be finite or infinite, formal or fuzzy, hierarchically ordered or not, and so on.

The basic operation of grouping elements into classes, which simplifies the world, is a very powerful operation, but it also raises many questions. In particular, a number of philosophers, from Socrates to Diderot and even post-modern philosophers, criticized such an operation (see, for instance, Foucault 1967). Indeed, this operation has multiple profits. First is the substitution of a rational and regular order in the chaotic and muddled multiplicities. Second is the reduction of the size of sets, so that, once we have constituted classes of equivalences, we can work with these classes and no more with the elements. Third, and finally, to make a partition of a set means locating in it a symmetry that decreases the complexity of the problem and so simplifies the world. We can say with Dagognet (1984, 1990) than “less is more”: to compress the data really brings an intellectual gain.

Having outlined the main reasons for classifications, let us see how these classifications have developed and which forms they got throughout the course of time.

2. A Brief History of Classifications

The history of classifications (Dahlberg 1976) develops in four periods. From Plato and Aristotle to the 18th century, ancient classifications are hierarchical ones, they are finite and generally based on one single criterion. During the 18th century, some new classifications appear, which are multicriteria – a domain can be co-divided in many ways, as Kant said in his Logic (see Kant 1988) – and indefinite or virtually infinite (Kant believed that we could endlessly subdivide the extension of a concept). At the end of the 18th and at the beginning of the 19th century, with the chemical classifications of Lavoisier and then of Mendeleyev, one discovers combinatorial classifications or multiple crossed orders, like the chemical table of Elements, which correspond to a new concept of classification. In the 20th century, through the progress of mathematical order theory, factorial analysis of correspondence, and automatic classification, formal models begin to develop.

a. From Antiquity to the Renaissance

French commentator of Greek philosophers, R. Joly said that a typical trend of the Greek spirit was to reduce a multiple and complex reality into some categories which satisfy the reason, both by their restricted number and by the clear and precise sense that becomes attached to each of them. Indeed, Plato and Aristotle are among the great classifiers of these ancient times.

In all of Plato’s Dialogues, and especially in the latest ones (Parmenides, Sophist, Politicus, Philaebus), Plato obviously classified a lot of things (ways of life, political constitutions, pleasures, arts, jobs, kinds of knowledge, and so forth). Generally, for Plato, things were classified in relation with the distance that separates them from their archetypal forms, which yields some order (or pre-order) on them. Plato’s classifications are finite, hierarchical, dichotomous, and based on a single criterion. For example, in Gorgias (465c), a set of all practices is divided into two classes, the practices concerning the body and the practices concerning the soul, each of them being then divided into two others: gymnastics and medicine, on one hand, and legislation and justice, on the other hand. In the same way, in Republic (510a), the whole universe, viewed as the set of all real things, is divided into the visible world and the invisible world, each class being subdivided into images and objects or living beings on one hand, mathematical objects and ideas, on the other hand.

According to Plato, the rules of classifications are very simple. First, we have to make symmetric divisions in order to get well-balanced classes. For example, if we classify the peoples, we have to avoid setting the Greek in front of the other peoples, because one of the classes will be plethoric while the other one will have only one element (Politicus, 262a). Second, As a good cook who cuts an animal─this metaphor is in the Phaedrus−it is also necessary to choose the good joints or articulations. For example, in the field of numbers, it would be senseless to set 1000 in front of 999 other numbers. In contrast, the opposition even/odd or prime/not prime, is a real one. Thirds, in general, we must also avoid using negative determinations. For example, we have to avoid determinations like not-A because it is impossible that the non-being has sorts or species, these determinations block the development of thought.

Plato did not observe these wise rules, so incurring Aristotle’s criticisms. Against Plato’s theory, Aristotle argues that the method of division is not a powerful tool because it is non-conclusive. It does not make syllogisms (First Analytics, I, 31). In another text (Second Analytics, II,5), Aristotle insists on the contingency of the passage from a predicate to another one, that is, in the Platonic division, for every new attribute, we can wonder why it is such an attribute oppose to another one. The differences introduced by dichotomies can be also purely negative and thus do not necessarily define a real being. Moreover, binary divisions presuppose that the number of the primitive species is a power of 2. In a division, a predicate can belong to different primitive species, for example “bipedalism” can apply to both birds and humans. But, according to Aristotle, the application of this term is not the same in both cases. Finally, the Platonic division confuses extensional and intensional views. It can identify the triangle, which is a kind, and one of its properties, for example, the equality of the sum of its angles in two right angles.

The previous questions get no answer in Plato’s theory. Aristotle rejected Plato’s method of division. But, Aristotle also rejected the Platonic doctrine of forms. According to Aristotle (Metaphysics, I, 9), Plato’s forms fail to explain how there could be permanence and order in the world. Far more, he argued, Plato’s theory of forms cannot explain anything at all in our material world. The properties that the forms have (according to Plato the forms are eternal, unchanging, transcendent, and so forth) are not compatible with material objects and the metaphor of participation or imitation breaks down in a number of cases. For instance, it is unclear what it mean for a white object to participate in, or to copy, the form of whiteness−that is, it is hard to understand the relationship between the form of whiteness and white objects themselves.

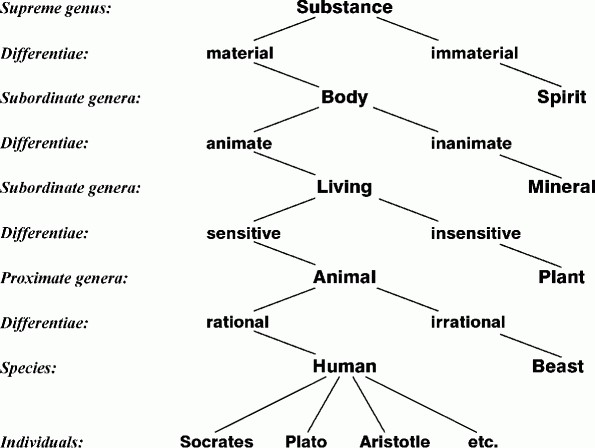
For all these reasons, Aristotle develops his own concepts, and his own logic of classifications. In the Topics (I, chap. 1), Aristotle introduces the notions of kind, species, property and a whole theory of basic predication that has subsequently developed in the work of Porphyry and Boece, respectively. This theory is based on the opposition between essence, all of the characters that define a thing, and accident, the qualities whose presence or absence does not modify the things essence. A commentator of the Aristotelian system, Porphyry (234-305), puts these distinctions to good use and tries to specify the hierarchy of the kinds and the species as defined by Aristotle. The famous Porphyrian Tree is the first abstract tree outlining these distinctions and illustrates the subordination existing between them (See Figure 1).

Figure 1: The Porphyrius Tree

In a passage of his Commentary on Aristotle’s Categories (2014) Porphyry asked good questions at the origin of a hotly-debated controversy over whether or not universals were physical or immaterial substances. That is, a contention over whether universals are separated from sensible things or if they are involved in them, finding their consistency therein. In opposition to the traditional views (Platonic and Aristotelian or scholastic realisms), other solutions appeared. For example, Nominalism (Roscelin, 11th c.) claimed that universals are but words and that nothing corresponds to them in the Nature, which knows only the singular. Against that was Conceptualism (Abélard, 12th cn. and Ockham, 14th cn.), the view that kinds exist as predicates of subjects that, themselves, are real. In the last centuries of Middle Ages and in the Renaissance, we find also great scholars who work on classification. In particular, Francis Bacon (1561-1626), whose work on the classification of knowledge that has inspired the great librarians of the 19th century. But, the logic of classifications, which remains, in this time, the Aristotelian logic, receives practically no new development until the 18th century.

b. From Classical Age to Victorian Taxonomy

In the Classical Age, taxonomy as a fully-fledged discipline began to develop for several reasons. One important reason emerges from the birth of natural science and the need to organize floras and faunas in connection with the growth of the human population on Earth, in the context of the beginning of agronomy (Dagognet, 1970). In this period, naturalists like Tournefort (1656-1708), Linnaeus (1707-1778), De Jussieu (1748-1836), Desfontaines (1750-1833) and Cuvier (1769-1832) tried to classify plants and animals all around the world.

When classifying things or beings, you must get a criterion or an index, in order to make classes and separate varieties inside the classes. Indeed, all those naturalists differ on the criteria of their classifications. For example, concerning the classification of plants, Tournefort chose corolla, while Linnaeus chose the sexual organs of the plant. Concerning the animals, the classification of Cuvier violates Aristotle’s recommendations, by compositing vertebrates and invertebrates which, by chance, are something real. At the end of the century, Kant summarizes, in his Logic (1800), the main part of the knowledge about classifications in this period, by specifying the definitions of a certain number of terms and operations that the naturalists of the time empirically use. Kant was only interested in the forms of the classifications. In his Logic he defines a logical division of a concept as “the division of all the possible contained in it”. The rules of this division are the following: 1) members of the division are mutually exclusive, 2) their union restores the sphere of the divided concept, 3) each member of the division can be itself divided (the division of such divided members is a subdivision). (1) and (2) seem to indicate that Kant was approaching our concept of a partition. But (3) shows that he does not have the concept of a chain of partitions, since he does not see that a subdivision of the same level forms one and the same partition.

These problems were also discussed, during the 19th century in Anglo-Saxon countries, even after Darwin’s theory of evolution. One may think that Darwin’s belief in branching evolution was based upon his familiarity with the taxonomy of his day, from which he was very aware. There were great taxonomists in England in the Victorian age and some of them−for instance, the paleontologist H. Alleyne Nicholson, a specialist of British Stromatoporoids−were prodigious and wrote monographs still in force today (Woodward 1903). At approximately the same time, H. Agassiz (Agassiz 1957), a scholar in classification theory, wrote about taxonomic concepts like categories, divisions, forms, homologies, analogies, and so on. Among different taxonomic systems mentioned in his Essay on Classification, include the classical systems of Leeuckart, Vogt, Linnaeus, Cuvier, Lamarck, de Blainville, Burmeister, Owen, Ehrenberg, Milne-Edwards, von Siebold, Stannius, Oken, Fitzinger, MacLeay, von Baer, van Bencden, and van der Hoeven. In The Origin of Species, Darwin himself said that it was a

truly wonderful fact…that all animals and all plants throughout all time and space should be related to each other in group subordinate to group, in the manner which we everywhere behold−namely, varieties of the same species most closely related together, species of the same genus less closely and unequally related together, forming sections and sub-genera, species of distinct genera much less closely related, and genera related in different degrees, forming sub-families, families, orders, subclasses, and classes. (1859, 128)

But what he called the “principle of divergence”–namely, the fact that during the modification of the descendants of any one species and during the incessant struggle of all species to increase in numbers, the more diversified these descendants become, the better will be their chance of succeeding in the battle of life−was illustrated by his famous tree-like diagram sketched in 1837 in the notebook in which he first posited evolution. From this time, tree-like structures, that has been also of great use in chemistry and would be formalized at the end of the century by the mathematician Arthur Cayley, tended to replace classifications.

c. The Beginning of Modernity

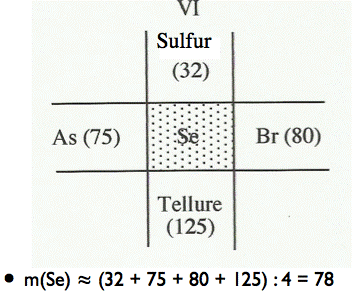
A new kind of classifications appeared at the end of the 18th century, with the development of Chemistry, namely, combinatorial classifications or cross multiple orders. This kind of classifications is either the crossing of two or more divisions, or the crossing of two or more hierarchies of divisions. In such a structure, as Granger (1967) said, “elements are distributed according to two or several dimensions, giving rise to a multiplication table”. In a combinatorial classification, the elements themselves are not necessarily distributed into classes. Only the components of these elements are classified. For Granger, this model refers to the Cartesian plane and to the ordinal principle on which it is based. The Cartesian plane, results from a will of ordering a certain distribution of points in the space, by ordering points in every row and then by ordering the rows themselves. The virtue of multiple orders is to place what is classified in the intersection of a line and a column. So, as Dagognet (1969) has shown, when an element is absent or there is an empty compartment, it can be defined by its surroundings. This is what happened in the Mendeleyev table. This table has two main advantages. First, the table is creative, so the mass of a chemical element can be calculated from those which surround it (see Figure 2), and hence, chemical elements, which did not exist in Nature but were synthesized only 30 years later in laboratories, have already been accounted for by Mendeleyev. Second, the classification is not a purely spatial picture of the world. The temporality, in particular the future, is already present in it.

Figure 2: The mass of an unknown element in the Mendeleyev Table

3. The Problem of Information Storage and Retrieval

At the end of the 19th century, the development of scientific research, which raised the question of information storage and retrieval, encouraged the constitution of voluminous librarian catalogues. This included the Dewey’s decimal classification, Otlet and La Fontaine’s universal decimal classification, and the Library of Congress classification. The aim of these kinds of classifications was to account for the whole of knowledge in the world. But, many problems arose from this attempt of library sciences to organize the whole knowledge. Three rules were commonly respected in more natural classifications: 1) Everything classified must appear in the catalogue (which must be, in principle, finite and complete), 2) there is no empty class, 3) nothing can belong to more than one class. Generally, these rules are not respected in library classifications. To face the extraordinary challenge of cataloguing knowledge growing indefinitely throughout the course of time, the big library classifications designed at the end of the 19th century adopted the principle of decimalization. This system was used because decimal numbers, used as numeral items, authorize indefinite extensions of classifications. Suppose you start with 10 main classes, from 0 to 9. If you add a zero to each number, you get the possibility of forming 100 classes (from 00 to 99) and if you go on, you can obtain 1000 classes (from 000 to 999). Then you can also put a comma or a point, and define items like: 150.234. After the point, the sequence of numbers is potentially infinite and you can go as far as is needed. Another difference is that library classifications can sometimes allow for vacant classes in their hierarchy, and also can, assume the inscription of classified subjects in several places. Vacant classes are used because a librarian must manage some place for new documents that are still temporarily unclassified. Multiple inscriptions are also used because readers, who sometimes do not know exactly what they are looking for, need to have a broad ranging accesses to knowledge. This made made way for the existence of entries like author, subject, time, place, and so forth. The previous requirement of decimalization is obvious in the Dewey Decimal Classification (DDC) proposed by Melvil Dewey in 1876 (Béthery 1982). This classification is made up of ten main classes or categories, each of them being divided into ten secondary classes or subcategories. These last ones contain in turn ten subdivisions. The partition of the ten main classes thus gives successively 100 divisions and 1000 sections.

DDC — main sections

000 – Computer Science, Information and General Works
100 – Philosophy and Psychology
200 – Religion
300 – Social Sciences
400 – Language
500 – Science (including Mathematics)
600 – Technology and Applied Science
700 – Arts and Recreation
800 – Literature
900 – History, Geography and Biography

In the same way, the Universal Decimal Classification (UDC) of Otlet and La Fontaine globally presents the same hierarchical organization, except in the fourth nodal class, which is left empty (thus, applying the previous principle of vacant classes).

As librarians have rapidly observed, one undesirable consequence of such decimal schemes is the increasing fragmentation of subjects as taxonomist’s work proceed. For example, the Dewey Classification, though having this useful advantage of being infinitely extendible, turns out rapidly to be a list or a nomenclature. This is also the case of the UDC of Otlet and La Fontaine, and of all the classifications of the same type. A first attempt to make up for such a disadvantage has consisted of allowing some junctions between categories in the classification. A second one is the possibility of using some tables (7 in the DDC) to aid in the search of a complex object, which may be located in different sites. For instance, a book of poetry, written by various poets from around the world, would appear in several classes, indexed thanks to the tables. In general, DDC used to combine elements from different parts of the structure, in order to construct a number representing the subject content. This one often combines 2 or more subject elements with linking numbers and geographical and temporal elements. The method consists of forming a new item rather than drawing upon a list containing each class and its meaning. For example, 330 (for Economics) + 9 (for Geographic Treatment) + 04 (for Europe) and the use of ‘/’ gives 330/94 (European Economy). Another example is the following: 973 (for United States) + 05 (division for periodicals) and the use of the point ‘.’ gives 973.05 (periodicals concerning the United States generally).

Other specific features occur in library classifications, which tend to make them very different from classical scientific taxonomies. One spectacular difference with hierarchical classifications in Zoology or Botany is, as we have already seen, that it is possible for subjects to appear in more than one class. For example, in DDC, a book on Mathematics could appear in the 372.7 section or in the 510 section, depending on if the book is a monograph instruction for teachers on how to teach mathematics, or a mathematics textbook for children. Another difference is a relative flexibility of library classifications.

Though there exist improvements, UDC and DDC, like most of the classifications constructed at the same time (see Bliss 1929) are based on a perception of knowledge and of the relationships between academic disciplines extant from 1890 to 1910. Moreover, though updated regularly, UDC and DDC, as decimal systems, are less hospitable to the addition of new subjects. These kinds of classification are based on fixed and historically dated categories. One may observe, for example, that none of the main concepts of our present library science (digital library, knowledge organization, automatic indexing, information retrieval, and so forth) were included in the index of the 2005 UDC edition, and that technical taxonomies generally require more complex features (Dobrowolski 1964).

4. Ranganathan and the PMEST Scheme

There have been many pursuits to solve the aforementioned librarian problems. Some of them are well known since the middle of the 20th century. In the course of the 20th century, new modes of indexing and original classification schedules appeared in library science with the Indian librarian Shiyali Ramamrita Ranganathan (1933, 2006) and his faceted classification – also called “Colon classification” (CC), because of its use of the colon to indicate relations between subjects in the former edition.

Ranganathan was at first a mathematician and knew little about the library. But he took charge of the Madras University Library, and was then deputed by his University to study Library Science in London. There, he attended the School of Librarianship in the University College and discovered, as he said later, the “charm of classifications”, and also its problems. He saw very quickly that Decimal Classifications did not give satisfaction to users. On the opposite, he had the vision of a meccano set, where, instead of having ready-made rigid toys, one can construct them with a few fundamental components. This made him think of a new kind of classification.

It appeared to Ranganathan that the new theory might be organized at the higher level in 5 fundamental categories (FC) called facets: Personality, Matter, Energy, Space and Time−in summary PMEST. In each isolate facet a Compound Subject is deemed to be a manifestation of one (and only one) of one or other of the five fundamental categories. There is also subfacets, so that the facet scheme PMEST and the subfacets we may form from it, are then used to sort subclasses in the main classes of the classification.

The difference with previous classifications is in the way one defines ‘subfacets’. Rather than simply dividing the main classes into a series of subordinate classes, one subdivides each main class by particular characteristics into facets. Facets, labeled by Arabic numbers, are then combined to make subordinate classes as needed. For example, Literature may be divided by the characteristic of language into the facet of Language, including English, German, and French. It may also be divided by form, which yields the facet of Form, including poetry, drama and fiction. So CC contains both basic subjects and their facets, which contain isolates. A basic subject stands alone, for example: Literature in the subject English Literature, while an isolate, in contrast, is a term that modifies a basic subject, for example, the term ‘English’. Every isolate in every facet must be a manifestation of one of the five fundamental categories in the PMEST scheme.

The advantages of the CC are numerous. The first one is a greater flexibility in determining new subjects and subject numbers. A second is the concept of phases, which allows taxonomists to readily combine most of the main classes in a subject. Consider for example a subject like Mathematics for biologist. In this case, single class number enumerative systems, as those predominating in US libraries, tend to force classifiers to choose either Mathematics or Biology as the main subject. However, CC supplies a specific notation to indicate this be-phased condition.

Indeed, some problems remain unsolved. In CC, facets, that is, small components of larger entities or units are similar to flat faces of a diamond which reflect the underlying symmetry of the crystal structure, so that the general structure of Ranganathan Classification, as that of a faceted classification in general, is a kind of permutohedron. In principle, all descriptions may be done, whatever the order of them. For example, if we have to classify a paper speaking about seasonal variations of the concentration of noradrenaline in the tissue of the rat, we must get the same access if we have the direct sequence: (1) Seasonal, variations, concentration, noradrenaline, tissue, rat, or the reversed one: (2) Rat, tissue, noradrenaline, concentration, variations, seasonal. In mathematical words, this means clearly that the underlying structure that makes this transformation possible must be a commutative group. But this is not always the case, and for some dihedral groups, this structure is even forbidden. Another potential worry is that the PMEST scheme, which certainly has some connections with Indian thought, is far from being universally accepted (see De Grolier 1962) and has not been very often implemented in libraries, even in India.

So, in spite of all the improvements they receive in the course of time, a lot of problems have been raised in front of library classifications. In particular, library classifications will be strongly questioned in the 20th century by the proliferating development of the knowledge. First, the ceaseless flux of new documents forbids a stiff topology for classifications. The problem, then, is to know how to construct evolutionary structures. Second, the successive orderings of the knowledge (groupings and revisions and not only ramifications) has called relational powerful and automated documentary languages. Classifications still remain necessary, because documentary languages cannot do everything. So the problem is still open. But, with the big development of mathematics in the last century, this general problem, which is the great problem of order, has to be investigated by the means of mathematical structures.

5. Order and Mathematical Models

First attempts to study orders in mathematics began to develop at the end of the 19th century with Peano, Dedekind and Cantor (especially with his theory of ordinals, which are linear ordered sets). They go on with Peirce (1880) and Shröder (1890) and their works around the question of an algebra of logic. Then, in the first part of the 20th century, comes the notion of partial order with an article of MacNeille (1937) and the famous work of G. Birkhoff (1967) who introduced the notion of lattice, algebraically developed later in the great book of Rasiowa and Sikorski (1970). During the same period, mathematical models of hierarchical classifications, which have been investigated in the USA by Sokal and Sneath (1963, 1973) or, in England, by Jardine and Sibson (1971) were developed in France in the works of Barbut and Monjardet (1970), Lerman (1970, 1981), and Benzécri (1973). All these works supposed the big last century advances in mathematical order theory: especially the papers of Birkhoff (1935), Dubreil-Jacotin (1939), Ore (1942, 1943), Krasner (1953-1954) and Riordan (1958). The Belgian logician Leo Apostel (1963) and the Polish mathematicians Luszczewska-Romahnowa and Batog (1965a, 1965b) have also published important articles on the subject. The more and more important use of computers in the search of automatic classifications has also been, in those years, a reason for searchers to get interested in mathematical models.

As there are many forms of classifications in the world of knowledge (we can find them, as we have seen, in mathematics, natural sciences, library and information science, and so forth) there are also many possible mathematical models for classifications. We begin with the study of extensional structures.

a. Extensional Structures

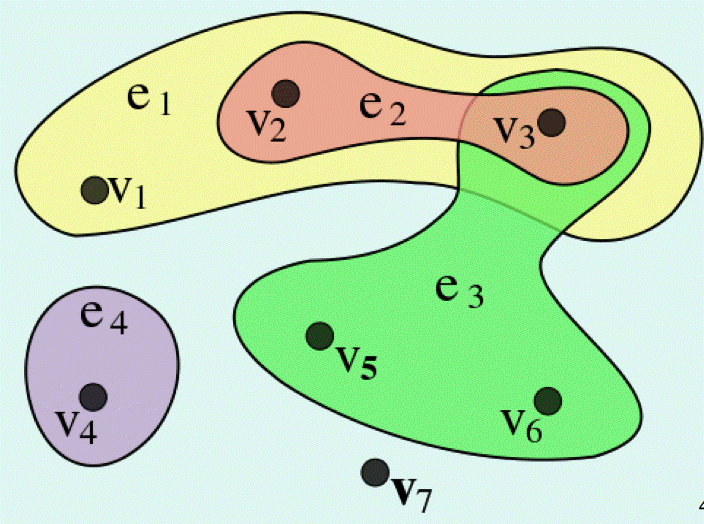
In order to clarify the situation, we start with the weakest form of them and move to stronger forms. Mathematics allows us to begin with very few axioms, that usually define weak general structures, and afterwards, by adding new conditions, one can get other properties and stronger models. In our case, the weakest structure is just a hypergraph H = (X,P) in the sense of Berge (1970), with X a set of vertices and P a set of nonempty subsets called edges (See Figure 3).

Figure 3: A Hypergraph

In this case, the set of edges P does not necessarily cover the set X, and some nodes (vertex of degree zero), may have no link to some edge. Assume the following conditions:

(C0) X ∈ P,

(C1) For all x ∈ P, {x} ∈ P,

Accordingly, we have a system of classes (in the sense of Brucker-Barthélemy 2007).

Add now the following new conditions: for every P_i ∈ P:

(C2) P_i ∩ P_j = Ø,

(C3) ∪ P_i= X,

Then P is a partition of X and the P_iare the blocks of the partition P.

Let now P(X) be the set of partitions on a nonempty finite set X. We may define on P(X) a partial order relation ≤ (reflexive, antisymmetric and transitive) such that P(X), ≤) is a lattice in the sense of Birkhoff (1967), that is, a partial order where every pair of elements has the same least upper bound and the same greatest lower bound. Then, one can prove that all the chains (all the linearly ordered sequences of partitions) of this lattice are equivalent to hierarchical classifications. So, the set C(X) of all these chains is exactly the set of all hierarchical classifications on a set. This set C(X) has itself a mathematical structure: it is a semilattice for set intersection. This model allows us to get all the possible partitions of P(X) and all the possible chains of C(X) (See Figure 4).

Figure 4: The lattice of partitions of a 4-element set.

A first problem is that such partitions are very numerous. For |X| = 9, for example, there is already 21147 partitions. So, when we want to classify some domain of objects (plants, animals, books, and so forth), it is not very easy to examine what classification is the best one among, say, several thousands of them.

A second problem is that the world is not made of chains of partitions. If it were, of course, the game would be over. Everything could be inserted in some hierarchical classification. But, the real world has no reason to present itself as a hierarchical classification. In the real world, we have generally to deal with quite chaotic entities, complicated fuzzy classes and poor structured objects, all that form what we can call ‘rough data’. So when we want to get a clear order, we have to construct it, such that it is extracted from the complicated data. For that, we have to compare objects, to know the degree to which they are similar, and to do so, we need of course a notion of ‘similarity’. In order to make empirical classifications we must evaluate the similarities or dissimilarities between elements to be classified. In the history of taxonomic science, Buffon (1749) and Adanson (1757) have tried to understand the meaning of this evaluation in the following way. First, they claim, we have to measure the distance between the objects by the means of some index, so that we can build classes. Afterwards, we have to measure the distance between classes themselves, so that we can group some classes into classes of classes, and so replace the initial set of objects with an ordered set of classes that is less numerous than them.

What old taxonomists were doing, only basis of observation, can now be carried out with the help of mathematics, using a modern notion of distance. Lerman (1970) and Benzécri (1973) showed that a hierarchical classification, that is, a chain of partitions, is nothing but a particular kind of distance or, a particular kind of dissimilarity (Van Cutsem 1994). It is an ultrametric distance, which gives tree representations (Barthélemy and Guénoche 1988) and also has the special property to correspond exactly with the chain, so that, when considering all the chains, the set of their corresponding distance matrices makes a semiring (R, +, ×) when we interpret the lattice operations min and max in an anusual but clever manner (+ for min, × for max) (Gondran 1976). Problems arise when the distance between the objects classified is not ultrametric. In such cases, we have to choose the closest ultrametric smaller than the given distance, and so, access to the best hierarchical classification we can get and which is the closest one to the data. However, this kind of approach leads, in general, to relatively unstable classifications.

Indeed, there are two kinds of instability for classifications. The first, Intrinsic instability,,is associated to the plurality of methods (distances, algorithms and so forth) that can be used to make the classifications of objects. The second is extrinsic instability, which is connected to the fact that our knowledge is changing with time, so the definitions of objects (or attributes of the objects) are evolving.

An answer to the question of intrinsic instability is a theorem of Lerman (1970) which says that if the number of attributes (or properties) possessed by the objects of a set X is constant, the associated quasi-order given by any natural metric is the same. But this result has two limits. First, when the sample variance of the number of attributes is a big one, of course, the stability is lost and second, if we classify the attributes, instead of classifying the objects, the reverse is not true.

For extrinsic instability the answers are more difficult to find. We may appeal to methods used in library decimal classifications (UDC, Dewey, and so forth), which make possible infinite ramified extensions, but these classifications, as we have seen, are apt to assume that higher levels are invariant and have also the disadvantage to be enumerative and to degenerate rapidly into simple lists. Also, pseudo-complemented structures (Hilman 1964) that admit some kinds of waiting boxes (or compartments) for indexing things that are not yet classified. We get as well structures whose transformations obey certain rules that have been fixed in advance. That is the case of Hopcroft 3-2 trees (Aho, Hopcroft, Ulmann 1983) for instance, or of structures close to these ones (Larson and Walden, 1979). In recent years, new models for making classifications came from conceptual formal analysis (Barwise and Seligman, 2003), computer science or views using non-classical logics in the domain of formal ontologies (Smith 1997, 2003). In computer science, for example, the concept of Abstract Data Type (ADT), related to the concept of Data Abstraction, important in object-oriented programming, may be viewed as a generalization of mathematical structures. An ADT is a mathematical model for data types, where a data type is defined by its behavior from the point of view of a user of the data. More formally, an ADT may be defined as a “class of objects whose logical behavior is defined by a set of values and a set of operations” (Dale-Walker 1996), which is strictly analogous to algebraic structures in mathematics. So, if we are not satisfied by a rough classification like the partition into collections, streams and iterators (support loops accessing data items) and relational data structures that capture relationships between data items, we must admit that ADT can also be regarded as a generalized approach of a number of algebraic structures, such as lattices, groups, and rings (Lidi 2004). Hence, classifications of ADT turn into classifications in algebraic specifications of ADT (Veglioni 1996). In this context, computer science adds nothing to mathematics and the problem is now that a classification of mathematical structures using, for instance, Category theory, as Pierce (1970) tried does not bring a sufficient answer because a category may exist while its objects are not necessarily constructible (Parrochia-Neuville 2013).

So, none of the previous approaches is very convincing for solving the basic problem, which always remains the same. We are lacking a general theory of classifications, which would only be able to study and, in the best case, solve some the main problems of classification.

b. A Glance at an Intensional Approach

Instead of making partitions by dividing a set of entities, so that the classes obtained in this way are extensional classes, as we saw in the previous section, we can instead proceed by associating a description to a set of entities. In this case, the classes are called intensional classes. Aristotle himself mixed the two points of view in his logic but Leibniz was the first to propose a purely intensional interpretation of classes. For a long time, that view was a minority and has never won unanimous support among the Ancient philosophers and logicians (as the numerous discussions between Aristotle and Plato, Ramus and Pascal, Jevons and Joseph demonstrate). However, the development of computer science brought this view back, since for declarative languages and particularly object-oriented languages, pure extensional classes or sets are rather uncommon. In this approach, the intension can be given either a priori, for example by a human actor from his knowledge of the domain, or a posteriori, when it is deduced from the analysis of a set of objects. In object-oriented modeling and programming, classes are traditionally defined a priori, with their extension mostly derived at running stage. This is usually done manually (intension being represented by logical predicates or tags), but techniques for a posteriori class discovery and organization also exist. In the context of programming languages, they deal with local class hierarchy modification by adding interclasses and use similarity-based clustering techniques or the Galois lattice approach (Wille 1996).

When there is an unrelated collection of sets, which is the case in artifact-based software classification, an issue is to compare and organize these sets simply by inclusion, or to apply conceptual clustering techniques. However, most of objected oriented languages are concerned with hierarchies, whose structure may be a tree, a lattice, or any partial order. The reason is that such structures reflect the variety of languages, some of them admitting multiple inheritance (C++, Eiffel), others only single inheritance (Smalltalk). Java has a special policy concerning this point: it admits two kinds of concepts, classes and interfaces, with single inheritance for classes and multiple inheritance for interfaces.

The viewpoint of Aristotle was the following: the division must be exhaustive, with parts mutually exclusive, and an indirect consequence of Aristotle’s principles is that only leaves of the hierarchy should have instances. Furthermore, the divisions must be based on a common concern whose modern name is the ‘discriminator’ in Unified Modeling Language (UML). But usual programming practices do not necessarily satisfy those principles. Multiple inheritance, for example, is contradictory with the assumption of mutually exclusive parts, and instances may in general be directly created from all (non-abstract) classes. Direct subclasses of a class can be derived according to different needs with different discriminators, but there is no evidence that this approach leads to relevant classifications. Objected oriented approaches, which transgress Aristotelian principles, are almost always practical storage modes but do not satisfy the main requisites of good classifications.

There are main principles that yield good classification, which are described in the intensional perspective. First–with Apostel [1963]– are some basic definitions.

From an intensional viewpoint, a division (or partition) is a closed formula F, which contains some assertion of the type (P ⊃ (Q₁ ∨ Q₂ ∨…∨ Q_n)). So, a classification is a sequence of implicative-disjunctive propositions which takes the following form: everything which has the property P has also one of the n properties Q₁… Q_n. Everything which has the property Q_r has also the property S, and so on (Apostel 1963, 188).

A division is essential if the individuals having the property P – and only this individual – may also have one of the properties Q_i. So, we can see that there are degrees in essentiality insofar as the number of individuals having the Q’s without having the P’s is greater or less. At every level, a classification may be probably or necessarily essential or exhaustive, or exclusive.

We call intensional weight w(P) of a property P, the set of disjunctions implied by this property (with necessity, factuality or probability). Properties defining classes in the same level may have extremely variable intensional weights. The basis of a division is the constant relation R, if any, between the properties of two different classes of this division.

A basis of division is (partially or totally) exhausted in some level insofar as, for this level, we do not find, in any case, true disjunctive propositions that are implied by the properties of this level and whose terms are connected by this very relation R.

A division is said to follow another one immediately (or to be immediately subsequent) if, for all P properties of the first, and for all Q properties of the second that are disjunctively implied by the P’s, there exists no sequence of R properties disjunctively implied by the P’s and disjunctively implying the Q’s.

The form of a property defining a class is the logical form of this property (conjunction of properties, disjunction of properties, negation of properties, single property).

For Apostel, an optimal classification should satisfy the following requisites:

Every level needs a basis for division;
No new basis for division shall be introduced before the previous one is exhausted;
Every division is essential;
Intensional weights of classes in a given level are comparable and relations between intensional weights of subsequent division properties in the classification must be constant.
Properties used to define classes are conjunctive ones, and not negative ones.
From the intensional viewpoint, divisions must be immediately subsequent.

In real domains, these requirements, or some of them, fail to hold. Levels are often extensionally equivalent but intensionally, the basis of division, the intensional weight, and so forth may change or not.

A natural classification is such that the definition of the domain classified determines in one and the same way the choice of the criteria of classification. It means that the fundamental set may be divided such that the division in the first level of the classification is an essential and subsequent one.

Intensional and extensional classifications are intimately related. Gathering entities in sets to produce extensional classes implies tagging these entities by their membership to these classes. But, intensional classes, built according to these descriptions, have an extension, which may be different from the initial extensional classes. So, in fact, both perspectives are not totally isomorphic and from Peirce (Hulwitt 1997) to Quine (1969), and presently, the question of natural classes remains an open and somewhat controversial question.

6. The Idea of a General Theory of Classifications

The idea of a general theory of classiﬁcations is not new. Such a project has been anticipated by Kant’s logic at the end of the 18th century. Then it was followed by many attempts to classify sciences at the beginning of the 19th century (Kedrov 1977) and had been posed by Auguste Comte in his Cours de philosophie positive (Comte 1975) as a general theory based on the study of symmetries in nature. Comte was inspired by mathematician Gaspard Monge and his classification of surfaces in geometry. However, this remains, in the work of Comte, a wishful thought. In the same way, the French naturalist Augustin-Pyramus de Candolle, published in 1813 an Elementary Theory of Botany, a book in which he introduced the term ‘taxonomia’, used in this work for the ﬁrst time (de Candolle 1813). De Candolle showed that Botany had to leave artiﬁcial methods for natural ones, in order to get a method independent from the nature of the objects. Unfortunately, nothing very concrete or precise followed his remarks. Moreover, the previous projects were only concerned with ﬁnite classiﬁcations, particularly, biological ones. A higher and more general view came into light around the 1960s with the Belgian logician Leo Apostel. Apostel (1963) wanted to write a concrete version of Set theory, and, in order to do that, needed axioms that allow him to include in the theory only the classes actually existing in the world. As such, Apostel was led to ask some questions about the well-known axioms of Zermelo-Fraenkel’s Set theory. He did not reject the whole ZF-axiomatics but however suspected axioms like the pairing axiom, the axiom of separation and the power set axiom. He also left optional the axiom of infinity and had rather a negative opinion about the axiom of choice. This project got a new revival with the recent book of Parrochia-Neuville (2013).

The hardships of solving the problem of instability of classifications provided motivation for a search for some clear composition laws to be defined on the set of classifications over a set and to a true algebra of classifications, if possible, which is very difficult because this algebra would have to be, in principle, commutative and non-associative. This search is all the more crucial that a recent theorem proved by Kleinberg (2002) shows that one cannot hope to find a classifying function which would be together scale invariant, rich enough and consistent. This result means that we cannot find empirical stable classifications by using traditional clustering methods.

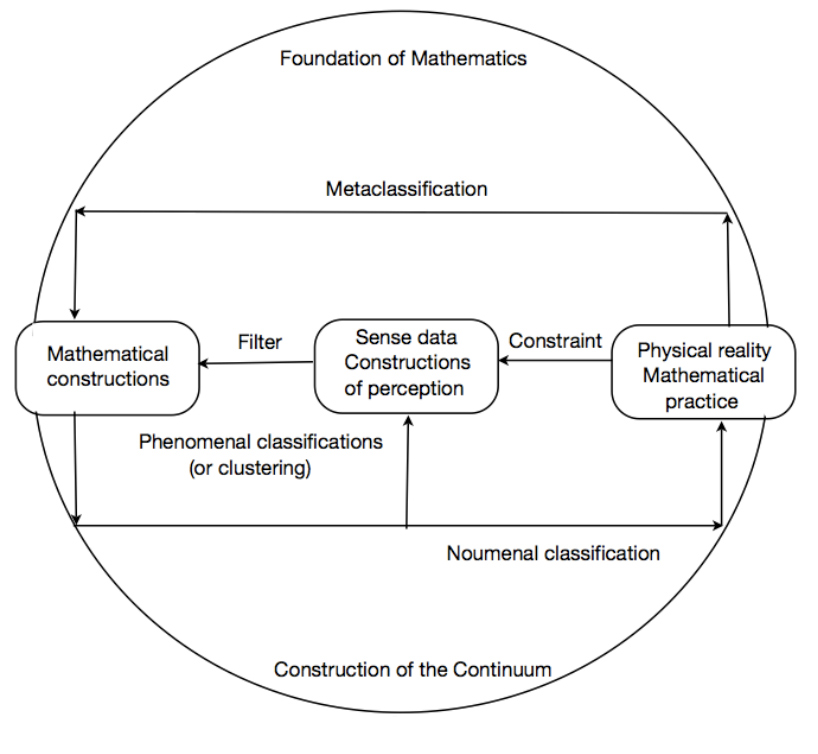
In the past, some attempts have been made to formalize non-commutative parenthesized products: Comtet (1970) and Neuville, in the 1980s used the Lukasiewicz’s Reverse Polish Notation (RPN), named also Postfix Notation, whose advantage is not only to make brackets or parentheses superfluous, but also to perform calculations on trees in the required order. But, a general algebra of classifications on a set is not known, even if some new models−Loday’s dendriform algebras, for example, which work very well for trees (See Dzhumadil’daev-Löfwall 2002)−are good candidates. In any event, we are invited to look for it, for two reasons. First, the world is not completely chaotic and our knowledge is evolving according to some laws. Second, there exist quasi-invariant classifications in physics (elementary particle classification), chemistry (Mendeleyev table of Elements), crystallography (the 232 groups of crystallographic structures) among others. Most of these good classifications are based on some mathematical structures (Lie groups, discrete groups, and so forth.). To address questions concerning classification theory, and clarify the different domains of it, one may propose this final view (See Figure 6):

When our mathematical tools apply only to sense data, we get phenomenal classifications (by clustering methods): these are generally quite unstable.
When our mathematical tools deal with crystallographic or quantum structures, we get what we call, using a Kantian concept, noumenal classifications (for instance, by invariance of discrete groups or Lie Groups). These are generally more stables.
When we search a general theory of classifications (including infinite ones), we are in the domain of pure mathematics. In this field, ordering and articulating the infinite set of classifications comes to construct the continuum.

Figure 6: Metaclassification

This problem is far from being solved because there are a lot of unstable theories (Shelah 1978, 1998). However, the recent work of Parrochia-Neuville (2013) assumes the conjecture that a metaclassification, that is, a classification of all mathematical schemes of classifications, does exist. The reason is that all these forms may be expressed as ellipsoids of an n-dimensional space (Jambu 1983) that must converge necessarily on a point, the index of the classification. If the real proof comes, this will give a theorem of existence of such a structure from which a number of important results could follow.

7. References and Further Readings

Adanson, M. 1757. Histoire naturelle du Sénégal. Paris: Claude-Jean-Baptiste Bauche.
Aho, A.V., Hopcroft, J.E, Ulmann, J.D. 1983. Data Structures and algorithms. Reading (Mass.): Addison-Wesley Publishing Company.
Agassiz, L. 1962. Essay on Classification (1857), reprint. Cambridge: Harvard University Press.
Apostel, L. 1963. Le problème formel des classifications empiriques. La Classification dans les Sciences. Gembloux: Duculot.
Aristotle, 1984. The Complete Works. Princeton: Princeton University Press.
Barbut M., Monjardet, B. 1970. Ordre et classifications, 2 vol. Paris: Hachette.
Barthélemy, J.-P., A. Guénoche. 1988. Les arbres et les représentations des proximités. Paris: Masson.
Barwise, J., Seligman, J. 2003. The logic of distributed systems. Cambridge: Cambridge University Press.
Béthery, A. 1982. Abrégé de la classification décimale de Dewey. Paris: Cercle de la librairie.
Bliss, H. E. 1929. The organization of knowledge and the system of the sciences. New York: H. Holt and Company.
Benzécri, J.-P., et alii. 1973. L’analyse des données, 1, La taxinomie, 2 Correspondances. Paris: Dunod.
Birkhoff, G. 1935. On the structure of abstract algebras. Proc. Camb. Philos. Soc. 31, 433-454.
Birkhoff, G. 1967. Lattice theory (1940), 3rd ed. Providence: A.M.S.
Brucker F., Barthélemy, J.-P. 2007. Eléments de Classification, aspects combinatoires et algorithmiques. Paris: Hermès-Lavoisier.
Buffon, G. L. Leclerc de, 1749. Histoire naturelle générale et particulière (vol. 1). Paris: Imprimerie royale.
Candolle (de), A. P. 1813. Théorie élémentaire de la Botanique ou exposition des principes de la classification naturelle et de l’art d’écrire et d’étudier les végétaux, first edition. Paris: Deterville.
Comte, A. 1975. Philosophie Première, Cours de Philosophie Positive (1830), Leçons 1-45. Paris: Hermann.
Comtet, L. 1970. Analyse combinatoire. Paris: P.U.F..
Dagognet, F. 2002. Tableaux et Langages de la Chimie (1967). Seyssel: Champ Vallon.
Dagognet, F. 1970. Le Catalogue de la Vie. Paris: P.U.F..
Dagognet, F. 1984. Le Nombre et le lieu. Paris: Vrin.
Dagognet, F. 1990. Corps réfléchis. Paris: Odile Jacob.
Dahlberg, I., 1976. Classification theory, yesterday and today. International Classification 3 n°2, pp. 85-90.
Dale, N., Walker, H. M. 1996. Abstract Data Types: Specifications, Implementations, and Applications. Lexington, Massachusetts: D.C. Heath and Company.
Darwin, C.R., 1964. On the Origin of Species (1859), reprint. Cambridge: Harvard University Press.
De Grolier, E. 1962. Etude sur les catégories générales applicables aux classifications documentaires, Unesco.
Dobrowolski, Z. 1964. Etude sur la construction des systèmes de classification. Paris, Gauthier-Villars.
Dubreil, P., Jacotin, M.-L. 1939. Théorie algébrique des relations d’équivalence. J. Math. 18, pp. 63-95.
Dzhumadil’daev,A. et Löfwall, C. 2002. Trees, free right-symmetric algebras, free Novikov Algebras and Identities. Homology, homotopy and Applications, vol.(4(2), pp. 165-190.
Foucault, M. 1967. Les Mots et les Choses. Paris: Gallimard.
Gondran, M. 1976. La structure algébrique des classifications hiérarchiques. Annales de l’Insee, pp. 22-23.
Granger, G.-G. 1980. Pensée formelle et Science de l’Homme (1967). Paris: Aubier-Montaigne.
Hilman, D.J. 1965. Mathematical classification technics for non static document collections, with particular reference to the problem of revelance. Classification Research, Elsinore Conference Proceedings, Munksgaard, Copenhagen, pp. 177-209.
Huchard, M., R. Godin, , A. Napoli, A. 2003. Objects and Classification. ECOOP 2000 Workshop reader, J. Malenfant, S. Moisan, A. Moreira (Eds), LNCS 1964. Berlin-Heidelberg-New York: Springer-Verlag, pp 123-137.
Hulswit, M. 1997. Peirce’s Teleological Approach to Natural Classes. Transactions of the Charles S. Peirce Society, pp. 722-772.
Jambu, M. 1983. Classification automatique pour l’analyse des données, 2 vol.. Paris: Dunod.
Jardine N., Sibson, R. 1971. Numerical Taxonomy. New York: Wiley.
Joly, R. 1956. Le thème philosophique des genres de vie dans l’Antiquité grecque. Bruxelles: Mémoires de l’Académie royale de Belgique, classe des Lettres et des Sciences mor. et pol., tome Ll, fasc. 3.
Kant, E. 1988. Logic. New York: Dover Publications.
Kedrov, B. 1977. La Classification des Sciences (vol. 2). Moscou: Editions du Progrès.
Kleinberg, J. 2002. An impossibility theorem for Clustering. Advances in Neural Information Processing Systems (NIPS), 15, pp. 463-470.
Krastner M. 1953-1954. Espaces ultramétriques et ultramatroïdes. Paris: Séminaire, Faculté des Sciences de Paris.
Larson, J.A., Walden, W.E. 1979. Comparing insertion shemes used to update 3-2 trees. Information Systems, vol.4, pp. 127-136.
Lerman, I.C. 1970. Les bases de la classification automatique. Paris: Gauthier-Villars.
Lerman, I.C. 1981. Classification et analyse ordinale des données. Paris: Dunod.
Lidi R., 2004. Abstract Algebra. Berlin-Heidelberg-New York: Springer-Verlag.
Luszczewska-Romahnowa S., Batog T. 1965a. A generalized classification theory I. Stud. Log., tom XVI, pp. 53-70.
Luszczewska-Romahnowa S., Batog T. 1965b. A generalized classification theory II. Stud. Log., tom XVII, pp. 7-30.
MacNeille 1937. Partially ordered sets. Transaction Amer. Math. Soc., vol. 42, pp. 416-460.
Ore O. 1942. Theory of equivalence relations. Duke Math. J. 9, pp. 573-627.
Ore O. 1943. Some studies on closer relations. Duke Math. J. 10, pp. 761-785.
Parrochia, D., Neuville, P. 2013. Towards a general theory of classifications. Bäsel: Birkhaüser.
Peirce C. S. 1880. On the Algebra of Logic. American Journal of Mathematics 3, pp. 15-57.
Pierce, R.S. 1970. Classification problems. Mathematical System theory, vol. 4, n°1, March, pp. 65-80.
Plato, 1997. The Complete Works. Cambridge: Hacking publishing Company
Porphyry, 2014. On Aristotle’s Categories. London, New York: Bloomsbury Publishing Plc.
Quine, W.V.O. 1969. Ontological Relativity and Other Essays. New York: Columbia University Press.
Ranganathan, S. R. 1933. Colon Classification. Madras: Madras Library Association.
Ranganathan, S. R. 2006. Prolegomena to Library Classification (1937), Reprint. New Delhi: Ess Pub..
Rasiowa H., Sikorski, R. 1970. The Mathematics of Metamathematics. Cracovia: Drukarnia Uniwersytetu Jagiellonskiego.
Riordan, J. 1958. Introduction to combinatorial analysis. New York: Wiley.
Roux, M. 1985. Algorithmes de classification. Paris: Masson.
Shelah, S. 1988. Classification Theory (1978). Amsterdam: North Holland.
Shröder, E. 1890. Vier Kombinatorische Probleme. Z. Math. Phys. 15, pp. 361-376.
Smith, B. 1997. Boundaries: An Essay in Mereotopology. L. Hahn (ed.), The Philosophy of Roderick Chisholm. La Salle, Open Court: Library of Living Philosophers, pp. 534-561.
Smith, B. 2003. Groups, sets and wholes. Revista di estetica, NS (P. Bozzi Festschrift), 24-3, 1209-130.
Sokal R. R., Sneath, P.H. 1963. Principle of numerical taxonomy. San Francisco: W. H. Freeman.
Sokal, R. R., and Sneath, P. H. 1973. Numerical Taxonomy, the principles and practice of numerical classifications. San Francisco: W. H. Freeman.
Van Cutsem B. (ed.) 1994. Classification and dissimilarity analysis. New York-Berlin-Heidelberg: Springer Verlag.
Veglioni, S. 1996. Classifications in Algebraic specifications of Abstract Data Types. CiteSeer^X
Windsor, M. P. 2009. Taxonomy was the foundation of Darwin’s evolution. Taxon 58, 1, pp. 43-49.
Wille, R. 1996. Restructuring lattice theory: an approach based on hierarchy of concepts. Rival, I (ed.) Ordered Sets. Boston: Reidel, pp. 445-470.
Woodward, H. 1903. Memorial to Henry Alleyne Nicholson. M.D., D.Sc., F.R.S. Geological Magazine, 10, pp. 451-452.

Author Information

Daniel Parrochia
Email: daniel.parrochia@wanadoo.fr
Université Jean Moulin – Lyon III
France

Internet Encyclopedia of Philosophy