Inconsistent Mathematics
Inconsistent mathematics is the study of commonplace mathematical objects, like sets, numbers, and functions, where some contradictions are allowed. Tools from formal logic are used to make sure any contradictions are contained and that the overall theories remain coherent. Inconsistent mathematics began as a response to the set theoretic and semantic paradoxes such as Russell’s Paradox and the Liar Paradox—the response being that these are interesting facts to study rather than problems to solve—and has so far been of interest primarily to logicians and philosophers. More recently, though, the techniques of inconsistent mathematics have been extended into wider mathematical fields, such as vector spaces and topology, to study inconsistent structure for its own sake.
To be precise, a mathematical theory is a collection of sentences, the theorems, which are deduced through logical proofs. A contradiction is a sentence together with its negation, and a theory is inconsistent if it includes a contradiction. Inconsistent mathematics considers inconsistent theories. As a result, inconsistent mathematics requires careful attention to logic. In classical logic, a contradiction is always absurd: a contradiction implies everything. A theory containing every sentence is trivial. Classical logic therefore makes nonsense of inconsistency and is inappropriate for inconsistent mathematics. Classical logic predicts that the inconsistent has no structure. A paraconsistent logic guides proofs so that contradictions do not necessarily lead to triviality. With a paraconsistent logic, mathematical theories can be both inconsistent and interesting.
This article discusses inconsistent mathematics as an active research program, with some of its history, philosophy, results and open questions.
Table of Contents
- Introduction
- Background
- Geometry
- Set Theory
- Arithmetic
- Analysis
- Computer Science
- References and Further Reading
1. Introduction
Inconsistent mathematics arose as an independent discipline in the twentieth century, as the result of advances in formal logic. In the nineteenth century, a great deal of extra emphasis was placed on formal rigor in proofs, because various confusions and contradictions had appeared in the analysis of real numbers. To remedy the situation required examining the inner workings of mathematical arguments in full detail. Mathematics had always been conducted through step-by-step proofs, but formal logic was intended to exert an extra degree of control over the proofs, to ensure that all and only the desired results would obtain. Various reconstructions of mathematical reasoning were advanced.
One proposal was classical logic, pioneered by Giuseppe Peano, Gottlob Frege, and Bertrand Russell. Another was paraconsistent logic, arising out of the ideas of Jan Łukasiewicz and N. A. Vasil’év around 1910, and first realized in full by Jaśkowski in 1948. The first to suggest paraconsistency as a ground for inconsistent mathematics was Newton da Costa in Brazil in 1958. Since then, his school has carried on a study of paraconsistent mathematics. Another school, centered in Australia and most associated with the name of Graham Priest, has been active since the 1970s. Priest and Richard Routley have forwarded the thesis that some inconsistent theories are not only interesting, but true; this is dialetheism.
Like any branch of mathematics, inconsistent mathematics is the study of abstract structures using proofs. Paraconsistent logic offers an unusually exacting proof guide that makes sure inconsistency does not get out of hand. Paraconsistency is not a magic wand or panacea. It is a methodology for hard work. Paraconsistency only helps us from getting lost, or falling into holes, when navigating through rough terrain.
a. An Example
Consider a collection of objects. The collection has some size, the number of objects in the collection. Now consider all the ways that these objects could be recombined. For instance, if we are considering the collection {a, b}, then we have four possible recombinations: just a, just b, both a and b, or neither a nor b. In general, if a collection has κ members, it has 2κ recombinations. It is a theorem from the nineteenth century that, even if the collections in question are infinitely large, still κ < 2κ, that is, the number of recombinations is always strictly larger than the number of objects in the original collection. This is Georg Cantor’s theorem.
Now consider the collection of all objects, the universe, V. This collection has some size,
|V|, and quite clearly, being by definition the collection of everything, this size is the absolutely largest size any collection can be. (Any collection is contained in the universe by definition, and so is no bigger than the universe.) By Cantor’s theorem, though, the number of recombinations of all the objects exceeds the original number of objects. So the size of the recombinations is both larger than, and cannot be larger than, the universe,
![]()
This is Cantor’s paradox. Inconsistent mathematics is unique in that, if rigorously argued, Cantor’s paradox is a theorem.
2. Background
a. Motivations
There are at least two reasons to take an interest in inconsistent mathematics, which roughly fall under the headings of pure and applied. The pure reason is to study structure for its own sake. Whether or not it has anything to do with physics, for example, Reimann geometry is beautiful. If the ideas displayed in inconsistent mathematics are rich and elegant and support unexpected developments that make deep connections, then people will study it. G. H. Hardy’s A Mathematician’s Apology (1940) makes a stirring case that pure mathematics is inherently worth doing, and inconsistent mathematics provides some panoramic views not available anywhere else.
The applied reasons derive from a longstanding project at the foundations of mathematics. Around 1900, David Hilbert proposed a program to ensure mathematical security. Hilbert wanted:
- to formalize all mathematical reasoning into an exact notation with algorithmic rules;
- to provide axioms for all mathematical theories, such that no contradictions are provable (consistency), and all true facts are provable (completeness).
Hilbert’s program was (in part) a response to a series of conceptual crises and responses from ancient Greece through Issac Newton and G. W. Leibniz (see section 6 below) to Cantor. Each crisis arose due to the imposition of some objects that did not behave well in the theories of the day—most dramatically in Russell’s paradox, which seems to be about logic itself.
The inconsistency would not have been such trouble, except the logic employed at that time was explosive: From a contradiction, anything at all can be proved, so Russell’s paradox was a disaster. In 1931, Kurt Gödel’s theorems showed that consistency is incompatible with completeness, that any complete foundation for mathematics will be inconsistent. Hilbert’s program as stated is dead, and with it even more ambitious projects like Frege-Russell logicism.
The failure of completeness was hard to understand. Hilbert and many others had felt that any mathematical question should be amenable to a mathematical answer. The motive to inconsistency, then, is that an inconsistent theory can be complete. In light of Gödel’s result, an inconsistent foundation for mathematics is the only remaining candidate for completeness.
b. Perspectives
There are different ways to view the place of inconsistent mathematics, ranging from the ideological to the pragmatic.
The most extreme view is that inconsistent mathematics is a rival to, or replacement for, classical consistent mathematics. This seems to have been Routley’s intent. Routley wanted to perfect an “ultramodal universal logic,” which would be a flexible and powerful reasoning tool applicable to all subjects and in all situations. Routley argued that some subjects and situations are intractably inconsistent, and so the universal logic would be paraconsistent. He wanted such a logic to underly not only set theory and arithmetic, but metaphysics, ecology and economics. (For example, Routley and Meyer [1976] suggest that our economic woes are caused by using classical logic in economic theory.) Rotuley (1980, p.927) writes:
There are whole mathematical cities that have been closed off and partially abandoned because of the outbreak of isolated contradictions. They have become like modern restorations of ancient cities, mostly just patched up ruins visited by tourists.
In order to sustain the ultramodal challenge to classical logic it will have to be shown that even though leading features of classical logic and theories have been rejected, … by going ultramodal one does not lose great chunks of the modern mathematical megalopolis. … The strong ultramodal claim—not so far vindicated—is the expectedly brash one: we can do everything you can do, only better, and we can do more.
A more restrained, but still unorthodox, view is of inconsistency as a non-revisionary extension of classical theory. There is nothing wrong with the classical picture of mathematics, says a proponent of this position, except if we think that the classical picture exhausts all there is to know. A useful analogy is the extension of the rational numbers by the irrational numbers, to get the real numbers. Rational numbers are not wrong; they are just not all the numbers. This moderate line is found in Priest’s work. As articulated by da Costa (1974, p.498):
It would be as interesting to study the inconsistent systems as, for instance, the non-euclidean geometries: we would obtain a better idea of the nature of certain paradoxes, could have a better insight on the connections amongst the various logical principles necessary to obtain determinate results, etc.
In a similar vein, Chris Mortensen argues that many important questions about mathematics are deeper than consistency or completeness.
A third view is even more open-minded. This is to see all theories (within some basic constraints) as genuine, interesting and useful for different purposes. Jc Beall and Greg Restall have articulated a version of this view at length, which they call logical pluralism.
c. Methods
There are at least two ways to go about mathematical research in this field. The first is axiomatic. The second is model theoretic. The axiomatic approach is very pure. We pick some axioms and inference rules, some starting assumptions and a logic, and try to prove some theorems, with the aim of producing something on the model of Euclid, or Russell and A. N. Whitehead’s Principia Mathematica. This would be a way of obtaining results in inconsistent mathematics independently, as if we were discovering mathematics for the first time. On the axiomatic approach there is no requirement that the same theorems as classical mathematics be proved. The hardest work goes into choosing a logic that is weak enough to be paraconsistent, but strong enough to get results, and formulating the definitions and starting assumptions in a way that is compatible with the logic. Little work has so far been done using axiomatics.
By far more attention has been given to the model theoretic approach, because it allows inconsistent theories to “ride on the backs” of already developed consistent theories. The idea here is to build up models—domains of discourse, along with some relations between the objects in the domain, and an interpretation—and to read off facts about the attached theory. A way to do this is to take a model from classical mathematics, and to tinker with the interpretation, as in collapsed models of arithmetic (section 5 below). The model theoretic approach shows how different logics interact with different mathematical structures. Mortensen has followed through on this in a wide array of subjects, from the differential calculus to vector spaces to topology to category theory, always asking: Under what conditions is identity well-behaved? Let Φ(a) be some sentence about an object a. Mortensen’s question is, if a = b holds in a theory, then is it the case that Φ(a) exactly when Φ(b)? It turns out that the answer to this question is extremely sensitive to small changes in logic and interpretations, and the answer can often be “no.”
Most of the results obtained to date have been through the model theoretic approach, which has the advantage of maintaining a connection with classical mathematics. The model theory approach has the same disadvantage, since it is unlikely that radically new or robustly inconsistent ideas will arise from always beginning at classical ideas.
d. Proofs
It is often thought that inconsistent mathematics faces a grave problem. A very common mathematical proof technique is reductio ad absurdum. The concern, then, is that if contradictions are not absurd—a fortiori, if a theory has contradictions in it—then reductio is not possible. How can mathematics be done without the most common sort of indirect proof?
The key to working inconsistent mathematics is its logic. Much hinges on which paraconsistent logic we are using. For instance, in da Costa’s systems, if a proposition is marked as “consistent,” then reductio is allowed. Similarly, in most relevance logics, contraposition holds. And so forth. The reader is recommended to the bibliography for information on paraconsistent logic. Independently of logic, the following may help.
In classical logic, all contradictions are absurd; in a paraconsistent logic this is not so. But some things are absurd nevertheless. Classically, contradiction and absurdity play the same role, of being a rejection device, a reason to rule out some possibility. In inconsistent mathematics, there are still rejection devices. Anything that leads to a trivial theory is to be rejected. More, suppose we are doing arithmetic and hypothesize that Φ. But we find that Φ has as a consequence that j=k for every number j, k. Now, we are looking for interesting inconsistent structure. This may not be full triviality, but 0 = 1 is nonsense. Reject Φ.
There are many consistent structures that mathematicians do not, and will never, investigate, not by force of pure logic but because they are not interesting. Inconsistent mathematicians, irrespective of formal proof procedures, do the same.
3. Geometry
Intuitively, M. C. Escher’s “Ascending, Descending” is a picture of an impossible structure—a staircase that, if you walked continuously along it, you would be going both up and down at the same time. Such a staircase may be called impossible. The structure as a whole seems to present us with an inconsistent situation; formally, defining down as not up, then a person walking the staircase would be going up and not up, at the same time, in the same way, a contradiction. Nevertheless, the picture is coherent and interesting. What sorts of mathematical properties does it have? The answers to this and more would be the start of an inconsistent geometry.
So far, the study has focused on the impossible pictures themselves. A systematic study of these pictures is being carried out by the Adelaide school. Two main results have been obtained. First, Bruno Ernst conjectured that one cannot rotate an impossible picture. This was refuted in 1999 by Mortensen; later, Quigley designed computer simulations of rotating impossible Necker cubes. Second, all impossible pictures have been given a preliminary classification of four basic forms: Necker cubes, Reutersvärd triangles, Schuster pipes or fork, and Ernst stairs. It is thought that these forms exhaust the universe of impossible pictures. If so, an important step towards a fuller geometry will have been taken, since, for example, a central theme in surface geometry is to classify surfaces as either convex, flat, or concave.
Most recently, Mortensen and Leishman (2009) have characterized Necker cubes, including chains of Neckers, using linear algebra. Otherwise, algebraic and analytic methods have not yet been applied in the same way they have been in classical geometry. Inconsistent equational expressions are not at the point where a robust answer can be given to questions of length, area, volume etc. On the other hand, as the Adelaide school is showing, the ancient Greeks do not have a monopoly on basic “circles drawn in sand” geometric discoveries.
4. Set Theory
Set theory is one of the most investigated areas in inconsistent mathematics, perhaps because there is the most consensus that the theories under study might be true. It is here we have perhaps the most important theorem for inconsistent mathematics, Ross Brady’s (2006) proof that inconsistent set theory is non-trivial.
Set theory begins with two basic assumptions, about the existence and uniqueness of sets:
- A set is any collection of objects all sharing some property Φ;
- Sets with exactly the same members are identical.
These are the principles of comprehension (a.k.a. abstraction) and extensionality, respectively. In symbols,
x ∈ {z : Φ(z)} ↔ Φ(x);
x = y ↔ ∀z (z ∈ x ↔ z ∈ y).
Again, these assumptions seem true. When the first assumption, the principle of comprehension, was proved to have inconsistent consequences, this was felt to be highly paradoxical. The inconsistent mathematician asserts that a theory implying an inconsistency is not automatically equivalent to a theory being wrong.
Newton da Costa was the first to develop an openly inconsistent set theory in the 1960s, based on Alonzo Church’s set theory with a universal set, or what is similar, W. V. O. Quine’s new foundations. In this system, axioms like those of standard set theory are assumed, along with the existence of a Russell set
R = {x : x ∉ x}
and a universal set
V = {x : x = x}.
Da Costa has defined “russell relations” and extended this foundation to model theory, arithmetic and analysis.
Note that V ∈ V, since V = V. This shows that some sets are self-membered. This also means that V ≠ R, by the axiom of extensionality. On the other hand, in perhaps the first truly combinatorial theorem of inconsistent mathematics, Arruda and Batens (1982) proved
![]()
where ∪R is the union of R, the set of all the members of members of R. This says that every set is a member of a non-self-membered set. The Arruda-Batens result was obtained with a very weak logic, and shows that there are real set theoretical theorems to be learned about inconsistent objects. Arruda further showed that
![]()
where P (X) denotes all the subsets of X and ⊆ is the subset relation.
Routley, meanwhile, in 1977 took up his own dialetheic logic and used it on a full comprehension principle. Routley went as far as to allow a comprehension principle where the set being defined could appear in its own definition. A more mundane example of a set appearing in its own defining condition could be the set of “critics who only criticize each other.” One of Routley’s examples is the ultimate inconsistent set,
x ∈ Z ↔ x ∉ Z.
Routley indicated that the usual axioms of classical set theory can be proven as theorems—including a version of the axiom of choice—and began work towards a full reconstruction of Cantorian set theory.
The crucial step in the development of Routley’s set theory came in 1989 when Brady adapted an idea from 1971 to produce a model of dialetheic set theory, showing that it is not trivial. Brady proves that there is a model in which all the axioms and consequences of set theory are true, including some contradictions like Russell’s, but in which some sentences are not true. By the soundness of the semantics, then, some sentences are not provable, and the theory is decidedly paraconsistent. Since then Brady has considerably refined and expanded his result.
A stream of papers considering models for paraconsistent set theory has been coming out of Europe as well. Olivier Esser has determined under what conditions the axiom of choice is true, for example. See Hinnion and Libert (2008) for an opening into this work.
Classical set theory, it is well known, cannot answer some fundamental questions about infinity, Cantor’s continuum hypothesis being the most famous. The theory is incomplete, just as Gödel predicted it would be. Inconsistent set theory, on the other hand, appears to be able to answer some of these questions. For instance, consider a large cardinal hypothesis, that there are cardinals λ such that for any κ < λ, also 2κ < λ. The existence of large cardinals is undecidable by classical set theory. But recall the universe, as we did in the introduction (section 1), and its size |V|. Almost obviously, |V| is such large a cardinal, just because everything is smaller than it. Taking the full sweep of sets into account, the hypothesis is true.
Set theory is the lingua franca of mathematics and the home of mathematical study of infinity. Since Zeno’s paradoxes it has been obvious that there is something paradoxical about infinity. Since Russell’s paradox, it has been obvious that there is something paradoxical about set theory. So a rigorously developed paraconsistent set theory serves two purposes. First, it provides a reliable (inconsistent) foundation for mathematics, at least in the sense of providing the basic toolkit for expressing mathematical ideas. Second, the mathematics of infinity can be refined to cover the inconsistent cases like Cantor’s paradox, and cases that have yet to be considered. See the references for what has been done in inconsistent set theory so far; what can be still be done in remains one of the discipline’s most exciting open questions.
5. Arithmetic
An inconsistent arithmetic may be considered an alternative or variant on the standard theory, like a non-euclidean geometry. Like set theory, though, there are some who think that an inconsistent arithmetic may be true, for the following reason.
Gödel, in 1931, found a true sentence G about numbers such that, if G can be decided by arithmetic, then arithmetic is inconsistent. This means that any consistent theory of numbers will always be an incomplete fragment of the whole truth about numbers. Gödel’s second incompleteness theorem states that, if arithmetic is consistent, then that very fact is unprovable in arithmetic. Gödel’s incompleteness theorems state that all consistent theories are terminally unable to process everything that we know is true about the numbers. Priest has argued in a series of papers that this means that the whole truth about numbers is inconsistent.
The standard axioms of arithmetic are Peano’s, and their consequences—the standard theory of arithmetic—is called P A. The standard model of arithmetic is N = {0, 1, 2, …}, zero and its successors. N is a model of arithmetic because it makes all the right sentences true. In 1934 Skolem noticed that there are other (consistent) models that make all the same sentences true, but have a different shape—namely, the non-standard models include blocks of objects after all the standard members of N. The consistent non-standard models are all extensions of the standard model, models containing extra objects. Inconsistent models of arithmetic are the natural dual, where the standard model is itself an extension of a more basic structure, which also makes all the right sentences true.
Part of this idea goes back to C. F. Gauss, who first introduced the idea of a modular arithmetic, like that we use to tell the time on analog clocks: On a clock face, 11 + 2 = 1, since the hands of the clock revolve around 12. In this case we say that 11 + 2 is congruent to 1 modulo 12. An important discovery in the late 19th century was that arithmetic facts are reducible to facts about a successor relation starting from a base element. In modular arithmetic, a successor function is wrapped around itself. Gauss no doubt saw this as a useful technical device. Inconsistent number theorists have considered taking such congruences much more seriously.
Inconsistent arithmetic was first investigated by Robert Meyer in the 1970’s. There he took the paraconsistent logic R and added to it axioms governing successor, addition, multiplication, and induction, giving the system R#. In 1975 Meyer proved that his arithemtic is non-trivial, because R# has models. Most notably, R# has finite models with a two element domain {0, 1}, with the successor function moving in a very tight circle over the elements. Such models make all the theorems of R# true, but keep equations like 0 = 1 just false.
The importance of such finite models is just this: The models can be represented within the theory itself, showing that a paraconsistent arithmetic can prove its own non-triviality. In the case of Meyer’s arithemetic, R# has a finitary consistency proof, formalizable in R#. Thus, in non-classical contexts, Gödel’s second incompleteness theorem loses its bite. Since 1976 relevance logicians have studied the relationship between R# and PA. Their hope was that R# contains PA as a subtheory and could replace PA as a stronger, more genuine arithmetic. The outcome of that project for our purposes is the development of inconsistent models of arithmetic. Following Dunn, Meyer, Mortensen, and Friedman, these models have now been extensively studied by Priest, who bases his work not on the relevant logic R but on the more flexible logic LP.
Priest has found inconsistent arithmetic to have an elegant general structure. Rather than describe the details, here is an intuitive example. We imagine the standard model of arithmetic, up to an inconsistent element
n = n + 1.
This n is suspected to be a very, very large number, “without physical reality or psychological meaning.” Depending on your tastes, it is the greatest finite number or the least inconsistent number. We further imagine that for j, k > n, we have j=k. If in the classical model j≠ k, then this is true too; hence we have an inconsistency, j=k and j≠ k. Any fact true of numbers greater than n are true of n, too, because after n, all numbers are identical to n. No facts from the consistent model are lost. This technique gives a collapsed model of arithmetic.
Let T be all the sentences in the language of arithmetic that are true of N; then let T(n) similarly be all the sentences true of the numbers up to n, an inconsistent number theory. Since T(n) does not contradict T about any numbers below n, if n > 0 then T(n) is non-trivial. (It does not prove 0 = 1, for instance.) The sentences of T(n) are representable in T(n), and its language contains a truth predicate for T(n). The theory can prove itself sound. The Gödel sentence for T(n) is provable in T(n), as is its negation, so the theory is inconsistent. Yet as Meyer proved, the non-triviality of T(n) can be established in T(n) by a finite procedure.
Most striking with respect to Hilbert’s program, there is a way, in principle, to figure out for any arithmetic sentence Φ whether or not Φ holds, just by checking all the numbers up to n. This means that T(n) is decidable, and that there must be axioms guaranteed to deliver every truth about the collapsed model. This means that an inconsistent arithmetic is coherent and complete.
6. Analysis
Newton and Leibniz independently developed the calculus in the 17th century. They presented ingenious solutions to outstanding problems (rates of change, areas under curves) using infinitesimally small quantities. Consider a curve and a tangent to the curve. Where the tangent line and the curve intersect can be though of as a point. If the curve is the trajectory of some object in motion, this point is an instant of change. But a bit of thought shows that it must be a little more than a point—otherwise, as a measure a rate of change, there would be no change at all, any more than a photograph is in motion. There must be some smudge. On the other hand, the instant must be less than any finite quantity, because there are infinitely many such instants. An infinitesimal would respect both these concerns, and with these provided, a circle could be construed as infinitely many infinitesimal tangent segments.
Infinitesimals were essential, not only for building up the conceptual steps to inventing calculus, but in getting the right answers. Yet it was pointed out, most famously by Bishop George Berkeley, that infinitesimals were poorly understood and were being used inconsistently in equations. Calculus in its original form was outright inconsistent. Here is an example. Suppose we are differentiating the polynomial f(x) =ax2+bx+c. Using the original definition of a derivative,
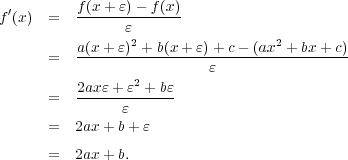
In the example, ε is an infinitesimal. It marks a small but non-trivial neighborhood around x, and can be divided by, so it is not zero. Nevertheless, by the end ε has simply disappeared. This example suggests that paraconsistent logic is more than a useful technical device. The example shows that Leibniz was reasoning with contradictory information, and yet did not infer everything. On the contrary, he got the right answer. Nor is this an isolated incident. Mathematicians seem able to sort through “noise” and derive interesting truths, even out of contradictory data sets. To capture this, Brown and Priest (2004) have developed a method they call “chunk and permeate” to model reasoning in the early calculus. The idea is to take all the information, including say ε = 0 and ε ≠ 0, and break it into smaller chunks. Each chunk is consistent, without conflicting information, and one can reason using classical logic inside of a chunk. Then a permeation relation is defined which controls the information flow between chunks. As long as the permeation relation is carefully defined, conclusions reached in one chunk can flow to another chunk and enter into reasoning chains there. Brown and Priest propose this as a model, or rational reconstruction, of what Newton and Leibniz were doing.
Another, more direct tack for inconsistent mathematics is to work with infinitesimal numbers themselves. There are classical theories of infinitesimals due to Abraham Robinson (the hyperreals), and J. H. Conway (the surreals). Mortensen has worked with differential equations using hyperreals. Another approach is from category theory. Tiny line segments (“linelets”) of length ϵ are considered, such that ϵ2 = 0 but it is not the case that ϵ = 0. In this theory, it is also not the case that ϵ ≠ 0, so the logical law of excluded middle fails. The category theory approach is the most like inconsistent mathematics, then, since it involves a change in the logic. However, the most obvious way to use linelets with paraconsistent logics, to say that both ϵ = 0 and ϵ ≠ 0 are true, means we are dividing by 0 and so is probably too coarse to work.
In general the concept of continuity is rich for inconsistent developments. Moments of change, the flow of time, and the very boundaries that separate objects have all been considered from the standpoint of inconsistent mathematics.
7. Computer Science
The questions posed by David Hilbert can be stated in very modern language:
Is there a computer program to decide, for any arithmetic statement, whether or not the statement can be proven? Is there a program to decide, for any arithmetic statement, whether or not the statement is true? We have already seen that Gödel’s theorems devastated Hilbert’s program, answering these questions in the negative. However, we also saw that inconsistent arithmetic overcomes Gödel’s results and can give a positive answer to these questions. It is natural to extend these ideas into computer science.
Hilbert’s program demands certain algorithms—a step-by-step procedure that can be carried out without insight or creativity. A Turing machine runs programs, some of which halt after a finite number of steps, and some of which keep running forever. Is there a program E that can tell us in advance whether a given program will halt or not? If there is, then consider the program E*, which exists if E does by defining it as follows. When considering some program x, E* halts if and only if x keeps running when given input x. Then
E* halts for E*
if and only if
E* does not halt for E*,
which implies a contradiction. Turing concluded that there is no E*, and so there is no E—that there cannot be a general decision procedure.
Any program that can decide in advance the behavior of all other programs will be inconsistent.
A paraconsistent system can occasionally produce contradictions as an output, while its procedure remains completely deterministic. (It is not that the machine occasionally does and does not produce an output.) There is, in principle, no reason a decision program cannot exist. Richard Sylvan identifies as a central idea of paraconsistent computability theory the development of machines “to compute diagonal functions that are classically regarded as uncomputable.” He discusses a number of rich possibilities for a non-classical approach to algorithms, including a fixed-point result on the set of all algorithmic functions, and a prototype for dialetheic machines.
Important results have been obtained by the paraconsistent school in Brazil—da Costa and Doria in 1994, and Agudelo and Carnielli in 2006. Like quantum computation, though, at present the theory of paraconsistent machines outstrips the hardware. Machines that can compute more than Turing machines await advances in physics.
8. References and Further Reading
a. Further Reading
Priest’s In Contradiction (2006) is the best place to start. The second edition contains material on set theory, continuity, and inconsistent arithmetic (summarizing material previously published in papers). A critique of inconsistent arithmetic is in Shapiro (2002). Franz Berto’s book, How to Sell a Contradiction (2007), is harder to find, but also an excellent and perhaps more gentle introduction.
Some of da Costa’s paraconsistent mathematics is summarized in the interesting collection Frontiers of Paraconsistency (2000)—the proceedings of a world congress on paraconsistency edited by Batens et al. More details are in Jacquette’s Philosophy of Logic (2007) handbook; Beall’s paper in that volume covers issues about truth and inconsistency.
Those wanting more advanced mathematical topics should consult Mortensen’s Inconsistent Mathematics (1995). For impossible geometry, his recent pair of papers with Leishman are a promising advance. His school’s website is well worth a visit. Brady’s Universal Logic (2006) is the most worked-out paraconsistent set theory to date, but not for the faint of heart.
If you can find it, read Routley’s seminal paper, “Ultralogic as Universal?”, reprinted as an appendix to his magnum opus, Exploring Meinong’s Jungle (1980). Before too much confusion arises, note that Richard Routley and Richard Sylvan, whose posthumous work is collected by Hyde and Priest in Sociative Logics and their Applications (2000), in a selfless feat of inconsistency, are the same person.
For the how-to of paraconsistent logics, consult both the entry on relevance and paraconsistency in Gabbay & Günthner’s Handbook of Philosophical Logic volume 6 (2002), or Priest’s textbook An Introduction to Non-Classical Logic (2008). For paraconsistent logic and its philosophy more generally see Routley, Priest and Norman’s 1989 edited collection. The collection The Law of Non-Contradiction (Priest et al. 2004) discusses the philosophy of paraconsistency, as does Priest’s Doubt Truth be a Liar (2006).
For the broader philosophical issues associated with inconsistent mathematics, especially in applications (for example, consequences for realism and antirealism debates), see Mortensen (2009a) and Colyvan (2009).
b. References
- Arruda, A. I. & Batens, D. (1982). “Russell’s set versus the universal set in paraconsistent set theory.” Logique et Analyse, 25, pp. 121-133.
- Batens, D., Mortensen, C. , Priest, G., & van Bendegem, J-P., eds. (2000). Frontiers of Paraconsistent Logic. Kluwer Academic Publishers.
- Berto, Francesco (2007). How to Sell a Contradiction. Studies in Logic v. 6. College Publications.
- Brady, Ross (2006). Universal Logic. CSLI Publications.
- Brown, Bryson & Priest, G. (2004). “Chunk and permeate i: the infinitesimal calculus.” Journal of Philosophical Logic, 33, pp. 379–88.
- Colyvan, Mark (2008). “The ontological commitments of inconsistent theories.” Philosophical Studies, 141(1):115 – 23, October.
- Colyvan, Mark (2009). “Applying Inconsistent Mathematics,” in O. Bueno and Ø. Linnebo (eds.), New Waves in Philosophy of Mathematics, Palgrave MacMillan, pp. 160-72
- da Costa, Newton C. A. (1974). “On the theory of inconsistent formal systems.” Notre Dame Journal of Formal Logic, 15, pp. 497– 510.
- da Costa, Newton C. A. (2000). Paraconsistent mathematics. In Batens et al. 2000, pp. 165–180.
- da Costa, Newton C.A., Krause, D´ecio & Bueno, Ot´avio (2007). “Paraconsistent logics and paraconsistency.” In Jacquette 2007, pp. 791 – 912.
- Gabbay, Dov M. & Günthner, F. eds. (2002). Handbook of Philosophical Logic, 2nd Edition, volume 6, Kluwer.
- Hinnion,Roland & Libert, Thierry (2008). “Topological models for extensional partial set theory.” Notre Dame Journal of Formal Logic, 49(1).
- Hyde, Dominic & Priest, G., eds. (2000). Sociative Logics and their Applications: Essays by the Late Richard Sylvan. Ashgate.
- Jacquette, Dale, ed. (2007). Philosophy of Logic. Elsevier: North Holland.
- Libert, Thierry (2004). “Models for paraconsistent set theory.” Journal of Applied Logic, 3.
- Mortensen, Chris (1995). Inconsistent Mathematics. Kluwer Academic Publishers.
- Mortensen, Chris (2009a). “Inconsistent mathematics: Some philosophical implications.” In A.D. Irvine, ed., Handbook of the Philosophy of Science Volume 9: Philosophy of Mathematics. North Holland/Elsevier.
- Mortensen, Chris (2009b). “Linear algebra representation of necker cubes II: The routley functor and necker chains.” Australasian Journal of Logic, 7.
- Mortensen, Chris & Leishman, Steve (2009). “Linear algebra representation of necker cubes I: The crazy crate.” Australasian Journal of Logic, 7.
- Priest, Graham, Beall, J.C. & Armour-Garb, B., eds. (2004). The Law of Non-Contradiction. Oxford: Clarendon Press.
- Priest, Graham (1994). “Is arithmetic consistent?” Mind, 103.
- Priest, Graham (2000). “Inconsistent models of arithmetic, II: The general case.” Journal of Symbolic Logic, 65, pp. 1519–29.
- Priest, Graham (2002). “Paraconsistent logic.” In Gabbay and Günthner, eds. 2002, pp. 287–394.
- Priest, Graham (2006a). Doubt Truth Be A Liar. Oxford University Press.
- Priest, Graham (2006b). In Contradiction: A Study of the Transconsistent. Oxford University Press. second edition.
- Priest, Graham (2008). An Introduction to Non-Classical Logic. Cambridge University Press, second edition.
- Priest, Graham, Routley, R. & Norman, J. eds. (1989). Paraconsistent Logic: Essays on the Inconsistent. Philosophia Verlag.
- Routley, Richard (1977). “Ultralogic as universal?” Relevance Logic Newsletter, 2, pp. 51–89. Reprinted in Routley 1980.
- Routley, Richard (1980). “Exploring Meinong’s Jungle and Beyond.” Philosophy Department, RSSS, Australian National University, 1980. Interim Edition, Departmental Monograph number 3.
- Routley, Richard & Meyer, R. K. (1976). “Dialectical logic, classical logic and the consistency of the world.” Studies in Soviet Thought, 16, pp. 1–25.
- Shapiro, Stewart (2002). “Incompleteness and inconsistency.” Mind, 111, pp. 817 – 832.
Author Information
Zach Weber
Email: zweber@unimelb.edu.au
University of Sydney, University of Melbourne
Australia
