Scientific Representation
To many philosophers, our science is intended to represent reality. For example, some philosophers of science would say Newton’s theory of gravity uses the theoretical terms ‘center of mass’ and ‘gravitational force’ in order to represent how a solar system of planets behaves—the changing positions and velocities of the planets but not their color changes. However, it is very difficult to give a precise account of what scientific representation is. More precisely, though, scientific representation is the important and useful relationship that holds between scientific sources (for example, models, theories, and data models) and their targets (for example, real-world systems, and theoretical objects). There is a long history within philosophy of describing the nature of the representational relationship between concepts and their objects, but the discussion on scientific representation started in the 20th century philosophy of science.
There are a number of different questions one can ask when thinking about scientific representation. The question which has received the most attention, and which will receive the most attention here, is what might be called (following Callendar and Cohen 2006, 68) the “constitution question” of scientific representation: “In virtue of what is there representation between scientific sources and their targets?” This has been answered in a wide variety of ways, some arguing that it is a structural identity or similarity which ensures representation while others argue that there is only a pragmatic relationship. Other questions about scientific representation relate more specifically to the ways in which representations are used in science. These questions are more typically asked directly about certain sorts of representational objects, especially scientific models, as well as from the perspective of sociology of science.
Table of Contents
- Substantive Accounts
- Deflationary and Pragmatic Accounts
- Model-Based Representation
- Sociology of Science
- References and Further Reading
1. Substantive Accounts
Scientific representation became a rising topic of interest with the development of the semantic view of theories which was itself developed partly as a response to the syntactic view of theories. Briefly, on the syntactic view, theoretical terms are defined in virtue of relationships of equivalence with observational entities (Suppe 1974). This was done through the creation of a first-order predicate calculus which contained a number of logical operators as well as two sets of terms, one set filled with theoretical terms and the other with observational terms. Each theoretical term was defined in terms of a correspondence rule linking it directly to an observational term. In this way a theoretical term such as ‘mass’ was given an explicit observational definition. This definition used only phenomenal or physical terms [such as “Drop the ball from the tower in this way” and “observe the time until the ball hits the ground”] plus logical terminology [such as ‘there is’ and ‘if…then’]; but the definition did not use any other theoretical terms [such as ‘gravitational force’ or ‘center of mass’]. The logical language also included a number of axioms, which were relations between theoretical terms. These axioms were understood as the scientific laws, since they showed relationships that held among the theoretical terms. Given this purely syntactic relationship between theory and observed phenomena, there was no need to give any more detailed account of the representation relationship that held between them. The correspondence rule syntactically related the theory with observations.
The details of the rejection of the syntactic view are beyond the scope of this article, but suffice it to say that this view of the structure of theories was widely rejected. With this rejection came a different account of the structure of theories, what is often called the semantic view. Since there was no longer any direct syntactic relationship between theory and observation, it became of interest to explain what relationship does hold between theories and observations, and ultimately the world.
Before examining the accounts of scientific representation that arose to explain this relationship, we should get a basic sense of the semantic view of theories. The common feature of the semantic approach to scientific theories was that they should not be thought of as a set of axioms and defined syntactic correspondence between theory and observation. Instead, theories are “extralinguistic entities which may be described or characterised by a number of different linguistic formulations” (Suppe 1974, 221). That is to say, theories are not tied to a single formulation or even to a particular logical language. Instead theories are thought of as being a set of related models. This is better understood through Bas van Fraassen’s (1980) example.
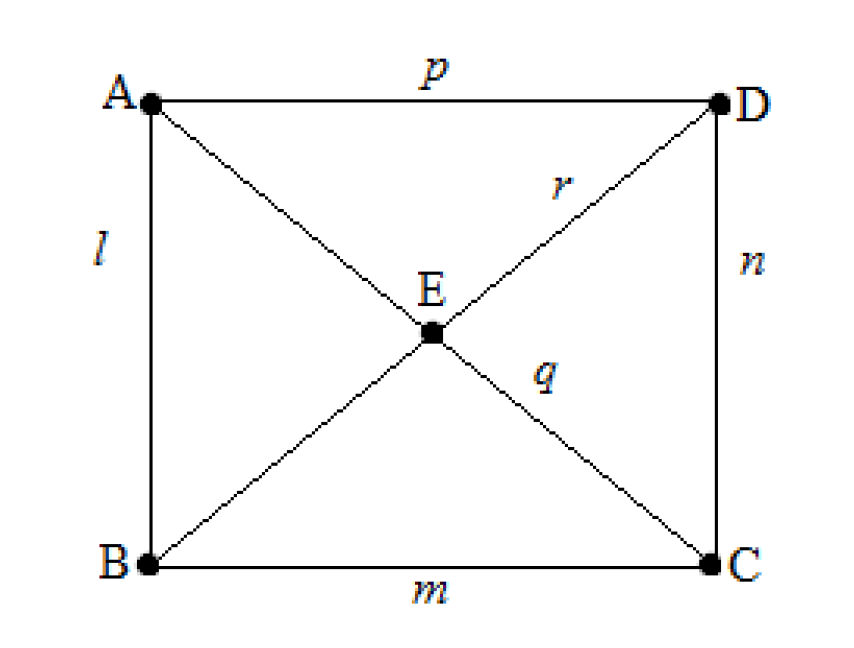
Van Fraassen (1980, 41-43) asks us to consider a set of axioms which are constituents of a theory which will be called T1:
A0 There is at least one line.
A1 For any two lines, there is at most one point that lies on both.
A2 For any two points, there is exactly one line that lies on both.
A3 On every line there lie at least two points.
A4 There are only finitely many points.
In Figure 1, we can see a model which shows that T1 is consistent, since each of the axioms is satisfied by this model.
Figure 1 – Model of Consistency of T1
Notice this is just one model which shows the consistency of T1, since there are other models which could be constructed to satisfy the axioms, like van Fraassen’s Seven Point Geometry (1980, 42). Note that what is meant here by ‘model’ is whatever “satisfies the axioms of a theory” (van Fraassen, 1980, 43). Another, perhaps more intuitive, way of expressing this is that a model for any theory T is any model which would make T true iff the model were the entirety of the universe. For example, if Figure 1 were the entirety of the universe, then clearly T1 would be true. Notice also that, on the semantic view, the axioms themselves are not central in understanding the theory. Instead, what is important in understanding a theory is understanding the set of models which are each truth-makers for that theory, insofar as they satisfy the theory.
This account of the structure of theories can be applied to an actual scientific theory, like classical mechanics. Here, following Ronald Giere (1988, 78-79), we can take up the example of the idealized simple systems in physics. These are, he argues, models for the theory of classical mechanics. For example, the simple harmonic oscillator is a model which is a truth-maker for (part of) classical mechanics. The simple harmonic oscillator can be described as a machine: “a linear oscillator with a linear restoring force and no others” (Giere 1988, 79); or mathematically: F = -kx. This model, were it the entirety of the universe, would make classical mechanics true.
The targets of theoretical models on the semantic view are not always real world systems. On some views, there is at least one other set of models which serve as the targets for theoretical models. These are variably called empirical substructures (van Fraassen 1980) or data models. These are ways of structuring the empirical data, typically with some mathematical or algebraic method. When scientists gather and describe empirical data, they tend to think of and describe it in an already partially structured way. Part of this structure is the result of the way in which scientists measure the phenomena while being particularly attentive to certain features (and ignoring or downplaying others). Another part of this structuring is due to the patterns seen in the data which are in need of explanation. On some views, most notably van Fraassen’s (1980), the empirical model is the phenomenon which is being represented. That is to say, there is no further representational relationship holding between data models and the world, at least as scientific practice is concerned (for a discussion of this, see Brading and Landry 2006). Others argue that the relationship between theoretical models and data models is only one of a number of interesting representational relationships to be described, which set themselves up in a hierarchical structure (French and Ladyman 1999, 112-114).
With this semantic account of the structure of scientific theories in place, there arose an interest to give an account of the representational relationship. The views which arose with the semantic view of theories are here called “substantive,” because they all attempt to give an account of the representational relationship which looks to substantive features of the source and target. Another way of putting this (following Knuuttila 2005) is to say that the substantive accounts of representation seek to explain representation as a dyadic relationship which holds between only the source and the target. As will be discussed below, this is different from the deflationary and pragmatic accounts which view scientific representation as at least a triadic relationship insofar as they add an agent to the relationship. There are two major classifications of substantive accounts of the representational relationship. The first are the structuralist views which are divided into three main types: isomorphism, partial isomorphism, and homomorphism. The second category is the similarity views.
a. Structuralist Views
Generically, the structuralist views claim that scientific representation occurs in virtue of what might be called “mapping” relationships that hold between the structure of the source and the structure of the target, i.e. the parts of the theoretical models point to the parts of the data models.
i. Isomorphism
Isomorphism holds between two objects provided that there is a bijective function—that is, both injective (or one-to-one) and surjective (or onto)—between the source and the target. Formally, suppose there are two sets, set A and set B. Set A is isomorphic to set B (and vice versa) if and only if there is a function, call it f, which could be constructed between A and B which would take each member of set A and map it to one and only one member of set B such that each member of set B is mapped.
To make the point more clear, let us suppose that set A is full of the capital letters of the English alphabet and set B is full of the natural numbers 1 through 26. We could create a function which, when given a letter of the alphabet, will output a number. Let’s make the function easy to understand and let f(A) = 1, f(B) = 2, and so on, according to typical alphabetical order. This function is bijective because each letter is mapped to one and only one number and every number (1 – 26) is being picked out by one and only one letter. Notice that since we can draw a bijective function from the letters to the numbers, we can also create one from the numbers to the letters: most simply, let f’(1) = A, f’(2) = B, and so on. Of course, there is nothing apart from the ease of our understanding which requires that we link A and 1, since we could have linked 1 with any letter and vice versa.
Isomorphism has frequently been used to explain representation (see van Fraassen 1980, Brading and Landry 2006). Since theories, on the semantic view, are a group of related models, there is a certain sort of structure that each of these models has. Most of the time, they are thought of as mathematical models though they need not be only mathematical as long as they have a structure. Van Fraassen also identifies what he calls “appearances,” which he defines as “the structures which can be described in experimental and measurement reports” (1980, 64). So, the appearances are the measurable, observable structures which are being represented (the targets of the representation). On van Fraassen’s account (1980), a theory will be successfully representational provided that there is an isomorphic relationship between the empirical substructures (the sources) and the appearances (as targets), and an isomorphic relationship between the theoretical models (as sources) and the empirical substructures (as targets). (Or at any rate, this is how he has commonly been interpreted (see Ladyman, Bueno, Suárez, and van Fraassen 2010)). As described by Mauricio Suárez (2003, 228), this isomorphism between the models shows that there is an identity that holds between the “relational framework of the structures” of the source and the target. And it is this relational framework of structures which is being maintained.
So, on the isomorphism view of scientific representation, some scientific theory represents some target phenomena in virtue of a bijective mapping between the structures of a theory and data, and a bijective mapping between the data and the phenomena. Notice that on the isomorphic view, the bijections which account for representation are external to the theoretical language. That is to say that the relationship that holds between the theory and the phenomena is not internal to the language in which the theory is presented. This is an important feature of this account because it allows for a mapping between very different kinds of structures. Presumably the (mainly mathematical) structures of theories are quite different from the structures of data models and are certainly very different from the structures of the phenomena (because the phenomena are not themselves mathematical entities). However, since the functions are external, we can create a function which will map these very different types of structures to one another.
ii. Partial Isomorphism
Isomorphism has much to suggest for it, especially when focusing in particular on those theories which are expressed mathematically. This is especially true in more mathematically-driven fields like physics. It seems that the mathematical models in physics are representing the structure that holds between various real world phenomena. For example, F=ma represents the way in which certain features of an object (its mass, the rate at which it is being accelerated) correspond to other features (its force). However, many philosophers (for example, Cartwright 1983 and Cartwright, Shomar, and Suárez 1995) have pointed out that there are cases where a theory or model truly represents some phenomena, even though there are features of the phenomena which do not have any corresponding structure in the theory or model, due to abstraction or idealization.
Take a rather simple example, the billiard ball model of a gas (French and Ladyman 1999). Drawing on Mary Hesse’s (1966) important work on models, French and Ladyman argue that there are certain features of the model which are taken to be representative, for example, the mass and the velocity of the billiard balls represent the mass and velocity of gas atoms. There are also certain features of the billiard balls which are non-representational, for example, the colors of the balls. Most importantly, though, as a critique of isomorphism, there are typically also some undetermined features of the balls. That is to say, for some of the features of the model, it is unknown whether they are representational or not. (For a more detailed scientific example, see Cartwright, Shomar, and Suárez 1995).
To respond to problems of this sort, many (French and Ladyman 1999; Bueno 1997; French 2003; da Costa and French 2003) have argued for partial isomorphism. The basic idea is that there are partial structures of a theory for which we can define three sets of members for some relation. The first set will be those members which do have the relevant relation, the second set will be those members which do not have that relation, and the third will be those members for which it is unknown whether or not they have that relation. It is possible to think of each of these sets of individuals as being a relation itself (since a relation, semantically speaking, is extensionally defined), and so we could draw a bijective function between these relations. But, as long as the third relation (the third set of individuals for which it was unknown whether or not they had the relation) is not empty, then the isomorphism will be only partial because there are some relations for which we are unsure whether or not they hold in the target.
As a more concrete example, consider the billiard ball and atom example from above. In order for there to be a partial isomorphism between the two, we must be able to identify two partial structures of each system, that is, a partial structure of the billiard ball model and a partial structure of the gas atoms. Between these partial structures, there must be a bijective function which maps relations of the model to relations of the gas-system. For example, the velocity of the billiard balls will be mapped to the velocity of respective atoms. There must be a second function which maps those non-representational relations of the model to features of the gas-system which are not being represented. For example, a non-representative feature of the model, like the color of the billiard balls, will be mapped to some feature of the system which is not being represented, like the non-color of the atoms. All the same, this will still remain partial because there will be certain relations that the model has which are unknown (or undefined) in relationship to the gas-system.
iii. Homomorphism
Homomorphism, defended by Bartels (2006), is more general than isomorphism insofar as all isomorphisms are homomorphisms, but not all homomorphisms are isomorphisms. Homomorphisms still rely on a function being drawn between two sets, but they do not require that the function be bijective; that is, the function need not be one-to-one or onto. So, this means that not every relation and part of the theory must map on to one and only one relation or part of the target systems. Additionally, this permits that there be parts and relations in the target system which are unmapped. Homomorphisms allow for a great deal of flexibility with regard to misrepresentations.
b. Similarity
Isomorphism (and the other -morphisms) places a fairly strict requirement on the relevant constitutive features of representation, which are on these views structural. But, as Giere points out (1988, 80-81), this is often not the relevant relationship. Oftentimes, scientists are working with theories or models which are valuable not for their salient structural features, but rather for some other reason. For example, when modeling the behavior of water flowing through pipes, scientists often model the water as a continuous fluid, even though it is actually a collection of discrete molecules (Giere 2004). Here, the representational value of the model is not between the structure of the model and the structure of the world (since water is structurally not continuous, but rather a collection of discrete molecules). Instead, the relevant representational value comes from a more general relationship which holds between the behavior of the modeled and real world systems. Giere suggests that what is needed is “a weaker interpretation of the relationship between model and real system” (1988, 81). His suggestion is that we explain representation in virtue of similarity. On his account a model will represent some real world system insofar as it is similar to the real world system. Notice that this is a much weaker account of representation than the structural accounts, since similarity includes structural similarities, and so encompasses isomorphism, partial isomorphism, and homomorphism.
Of course, if we try hard enough, we can notice similarities between any two objects. For example, any two material objects are similar at least insofar as they are each material. Thus, Giere suggests that an account of scientific representation which appeals to similarity requires an “implicit” (or explicit) “specification of relevant respects and degrees” (81). Respects indicate the relevant parts and ways in which the model is taken to be representative. Perhaps it is some dynamical relationship expressed in an equation; perhaps it is some physical similarity that exists between some tangible model and some target object (for example, a plastic model of a benzene ring); perhaps it is the way in which two parts of a model are able to interact with one another, which shows how two objects in the target system might interact (like the relevant behavior of the model of water flowing through pipes). The limitations with regard to claims of the respects of similarity are limited only by what scientists know or take to be the case about the model and the target system. For example, a scientist could not claim that there was a similarity between the color of a benzene model and a benzene ring since benzene rings have no color. Similarly, a scientist could not claim that there is similarity between the color of a mathematical model and the color of a species of bacteria since a mathematical model does not have any color. Notice that it is insufficient to merely specify the respects in which a model is similar since similarity can come in degrees. Of course, there is a whole spectrum of degrees of similarity on which any particular similarity can fall. A source can be anywhere from an extremely vague approximation of its target to being nearly identical to its target (what Giere calls “exact” (1988, 93)) and everywhere in between.
Giere’s own example is that, “The positions and velocities of the earth and moon in the earth-moon system are very close to those of a two-particle Newtonian model with an inverse square central force” (1988, 80). Here, the relevant respects are the position and velocity of the earth and moon. The relevant degree is that the positions and velocities in the earth-moon system are “very close” to the two-particle Newtonian model. These respects and degrees thus give us an account of how we should think of the similarity between the model and the target system.
Giere uses similarity to describe the relationship between models and the real-world systems they represent, and sometimes between different models (one model may be a generalization of another, and so on). Theories themselves are constituted by a set of these models as well as some hypotheses that link the models to the real world which define the respect and degree of the similarity between the models and their targets.
More recently, Michael Weisberg (2013) has argued for a similarity account of representation. In brief, his view argues that two sets of things be distinguished in both source and target: the attributes and the mechanisms. In distinguishing these sets, an equation can be written in which the common attributes and mechanisms can be thought of as the intersection of the attributes of the model and of the target system, and the intersection of the mechanisms of the model and target system. The dissimilarities can also be identified in a similar fashion. He adds some terms to these sets which are weighting terms and functions. These allow the users to indicate which similarities are more important than others. Rewriting the equation as a ratio between similarities and dissimilarities will result in a method by which we can make comparative judgments about different models. In this way, we will be able to say, for example, that one model is more or less similar than another.
c. Critiques of Substantive Accounts
While similarity and isomorphism continue to have some support in the contemporary literature (especially in modified versions; see below, section 3c), the versions described above have faced serious criticisms. One of the most common arguments against the substantive views is that they are unable to handle misrepresentations (Suárez 2003, 233-235; Frigg 2006, 51). Many models in science do not accurately reflect the world, and, in fact, the model is often viewed as particularly useful because of (not in spite of) the misrepresentations. Nancy Cartwright (1983) has famously argued for a fictional account of modelling and made this case for the laws of physics. Others have shown that similar things are true in other scientific domains (Weisberg 2007a). When the theories are intentionally inaccurate, there will be difficulty in explaining the way in which these theories are representational (as scientists and philosophers often take them to be), with reference to isomorphism or similarity.
Suárez (2003, 235-237) has also argued that both similarity and isomorphism are each neither necessary nor sufficient for representation. Consider first isomorphism. It must be the case that it is not necessary for representation, given that scientists often take certain theories to be representative of their real-world targets even though there is no isomorphic relationship between the theory and the target system. The same is true of similarity. Using his example, suppose that there is an artist painting an ocean view, using some blue and green paints. This painting has all sorts of similarities to the ocean view she is representing, one of which is that both the painting and the ocean are on the same relative side of the moon, are both in her line of vision at time t, share certain colors, and so forth. But which ones are relevant to its being representative and which are more contingent is up to the discretion of the agent who takes it to be representative of the ocean view in certain respects (as Giere argued). But if this is the case, then it turns out that A represents B if and only if A and B are similar in those respects in which A represents B. This ultimately leaves representation unexplained.
Supposing we can give some account of salience or attention or some other socially-based response to this first problem (which seems possible), we are left with the problem that plenty of salient similarities are non-representational. Suárez makes this point with Picasso’s Guernica (2003, 236). The bull, crying mother, eye, knife, and so forth, are all similar to certain real-world objects. But the painting is not a representation of these other things. It is representing some of the horrible atrocities of Franco.
Suárez also argues that both similarity and isomorphism are insufficient for representation. Consider the first, similarity. Take any given manufactured item, for example, an Acer C720 Chromebook, a computer which is similar to many other computers (hundreds of thousands). Notice that the fact of its similarity is insufficient to make it represent any of the other computers. Even if we add in Giere’s requirement that there be hypotheses which define the respects and degrees of the similarity, the insufficiency will remain. In fact, it seems as though there are hypotheses which define the relevant respects and degrees of similarity between the computers: Acer’s engineers and quality control have made sure that the production of these computers will result in similar computers. All the same, even with these hypotheses which give respects and degrees, we would not want to say that any given computer represents the others.
The non-sufficiency problem holds for isomorphism as well. Suppose someone were to write down some equation which had various constants and variables, and expressed certain relationships that held between the parts of the equation. Suppose now that, against all odds, this equation turns out to be isomorphic to some real-world system, say, that it describes the relationship between rising water temperatures and the reproduction rate of some species of fish which is native to mountain streams in the Colorado Rockies. To many, it appears to be counterintuitive to think that representations could happen accidentally. However, if isomorphism is sufficient for representation, then we would have to admit that the randomly composed equation does represent this fish species, even if no one ever uses or even recognizes the isomorphic relationship.
There are other arguments against these views in general, an important one being that they lack the right logical properties. Drawing on the work of Goodman (1976), both Suárez (2003, 232-233) and Roman Frigg (2006, 54) argue that representation has certain logical properties which are not shared by similarity or isomorphism. Representation is non-symmetric, so when some A represents B, it does not follow that B represents A. Representation is non-transitive: if A represents B and B represents C, it does not follow that A represents C. It’s also non-reflexive: A does not represent itself. Since isomorphism is reflexive, transitive, and symmetric, and similarity is reflexive and symmetric, they do not have the properties required to account for representation.
There are replies to these arguments on behalf of the substantive views. First, there is a general question about whether or not we are justified in making inferences from representation in art to representation in science. As was discussed above, many of the criticisms against substantive views draw examples from the domain of art (for example, Suárez’s (2003) uses many examples of paintings and is drawing upon Goodman’s (1976) which discusses representation in art). But, it should not be taken as given that what holds in art must translate to science. In fact, in many cases, the practices in art seem to be quite different from the practices in science. As Bueno and French say, “After all, what do paintings—in particular those that are given as counter-examples to our approach, which are drawn from abstract art—really have to do with scientific representation?” (2011, 879).
Following Anjan Chakravaratty (2009), Otávio Bueno and French (2011) argue that something like similarity or partial isomorphism is, in fact, necessary for successful representation in science. If there were no similarity or isomorphism at all, the successful use of models “would be nothing short of a miracle” (885). That is to say, while similarity or partial isomorphism might not be the whole story, they are at least part of the story. Using the aforementioned example of Picasso’s Guernica, they note that “there has to be some partial isomorphism between the marks on the canvass and specific objects in the world in order for our understanding of what Guernica represents to get off the ground” (885).
Replies have been made to the other arguments as well. Bueno and French (2011) argue that their account of partial isomorphism can meet all of the criticisms raised by Suárez (2003) and Frigg (2006). Adam Toon (2012) discusses some of the ways in which supporters of a similarity account of representation might respond to criticisms. Bartels (2006) defends the homomorphism account against these criticisms.
2. Deflationary and Pragmatic Accounts
If, as these scholars have argued, these substantive views will not work to explain scientific representation, what will? Suárez (2015) argues that what is needed instead is a deflationary account. A deflationary account claims “that there is no substantive property or relation at stake” (37) in debates about scientific representation. Deflationary accounts are typically marked by a couple of features. First, a deflationary account will deny that there are any necessary and sufficient conditions of scientific representation, or if there are, they will lack any explanatory value with regard to the nature of scientific representation. Second, these accounts will typically view representation as a relationship which is deeply tied to scientific practice. As Suárez puts it, “it is impossible, on a deflationary account, for the concept of representation in any area of science to be at variance with the norms that govern representational practice in that area…representation in that area, if anything at all, is nothing but that practice” (2015, 38).
Already we can see that these views will be quite different from the substantive views. Each of these views was substantive in the sense that they gave necessary and sufficient conditions for representation. There was also a distinct way in which these views were detached from scientific practice, since whether something was representational had little to do with whether or not it was accepted by scientists as representational and more to do with the features of the source and target. In each case, it was a relationship that was entirely accounted for by features of the theory or model and the target system. As Knuuttila (2005) describes it, these were all dyadic (two-place) accounts insofar as the relationship held between only two things. The deflationary accounts take a markedly different direction by moving to at least a triadic (three-place) account of representation.
In some cases, the views that have developed have followed the general lead of many deflationary views in giving a central role to the work of an agent in representation. These views do not qualify as deflationary, given that they still give necessary and sufficient conditions of representation. Given the importance of the role of agents and aims, we might call these views pragmatic. Although pragmatic and deflationary views are importantly distinct in their aims, they share many common threads and in many cases, the views could be reinterpreted as deflationary or pragmatic with little effort. As such, they will be grouped together in this section.
a. DDI
The earliest deflationary account of representation was RIG Hughes’ DDI Account (1997). The DDI Account consists of three parts: denotation, demonstration, and interpretation. Denotation is the way in which a model or theory can reference, symbolize, or otherwise act as a stand-in for the target system. The sort of denotation being invoked by Hughes is broad enough to include the denotation of concrete particulars (for example, a model of the solar system will denote particular planets), the denotation of specific types (for example, Bohr’s theory models not just this hydrogen atom, but all hydrogen atoms), and the denotation of a model of some global theory (for example, this particular model is “represented as a quantum system” (S331)). In each case, the model denotes something else; it stands in for some particular concrete object, some type of theoretical object, or some type of dynamical system.
We might think this relationship sufficient for representation, since the fact that scientists treat certain objects or parts of models as being stand-ins or symbols for some target system seems to answer the question of the relationship between a model and the world. Hughes, though, thinks that in order to understand scientific representation, we need to examine how it is actually used in scientific practice. This requires additional steps of analysis. The second part of Hughes’ DDI Account is demonstration. This is a feature by which models “contain resources which enable us to demonstrate the results we are interested in” (S332). That is, models are typically “representations-as,” meaning not only do scientists represent some target object or system, but they also represent it in a certain way with certain features made to be salient. The nature of this salience is such that it allows users to draw certain types of conclusions and make certain predictions, both novel and not. This is demonstration in the sense that the models are the vehicles through which (or in which) these insights can be drawn or demonstrated, physically, geometrically, mathematically, and so forth This requires that they be workable or used in certain ways.
The final part of the DDI Account is interpretation. It is insufficient that the models demonstrate some particular insight. The insight must be interpreted in terms of the target system. That is to say, scientists can use the models as vehicles of the demonstration, but in doing so, part of the representational process as defended in the DDI Account is that scientists interpret the demonstrated insights or results not as features of the model, but rather as features which apply to the target system (or at least, the way scientists are thinking of the target system).
In summary, with denotation, we are moving in thought from some target system to a model. We take a model or its parts to stand in or symbolize some target system or object. In demonstration, we use the model as a vehicle to come to certain insights, predictions, or results with regard to the relationship that holds internal to the model. It is in interpretation that we move from the model back to the world, taking the results or insights gained through use of the model to be about the target system or object in the world.
b. Inferential
i. Suárez
After criticizing the substantive accounts in his (2003), Suárez (2004) developed his own account of representation which focused centrally on inference and inferential capacities, what he calls an inferential conception of representation. As he describes it there, this account involves two parts. The first part is what he calls representational force. Representational force is defined as “the capacity of a source to lead a competent and informed user to a consideration of the target” (2004, 768). Representational force can exist for a number of reasons. One way to get representational force is to repeatedly use the source as a representation of the target. Another way is in virtue of intended representational uses, that is, in virtue of the intention of the creator or author of some source viewed within the context of a broader scientific community. Oftentimes, the representational force will occur as a combination of the two. It is also a contextual property, insofar as it requires that the agent using the source has the relevant contextual knowledge to be able to go from the source to the (correct/intended) target.
So, for example, in the upper left-hand corner of my word processor is a little blueish square with a smaller white square and a small dark circle inside of it (it is supposed to be an image of a floppy disk). This has representational force insofar as it allows me to go from the source (the image of the floppy disk) to the target (a means of saving the document which I am currently writing). In this case, the representational force exists in virtue of both the intended representational uses (the creators of this word processor surely intend this symbol to stand in for this activity) as well as repeated uses (I am part of a society which has, in the past, repeatedly used an image of a floppy disk to get to this target, not only in this program but in many others as well). It is also contextual: someone who had never used computers would not have the requisite knowledge to be able to use the icon correctly.
This is part of the story for Suárez, but in order to have scientific representation there must be something more than mere representational force. On his view, scientific representations are subject to a sort of objectivity which does not necessarily exist for other representations, for example, the example above of the save icon. The objectivity is not meant to indicate that there is somehow an independent representational relationship that exists in the world when scientists are engaged in scientific representation. Instead, the objectivity is present insofar as representations are constrained in various ways by the relevant features of the targets system which is being represented. That is, because there is some real feature which scientists are intentionally trying to represent in their scientific models and theories, the representation cannot be arbitrary but must respond to these relevant features. So the constraints are themselves objective, but this does not commit Suárez to identifying some reified relationship that holds between sources and targets.
According to Suárez, if we are going to get this objectivity in representations, we must turn to a second feature: the capacity of a source to allow for surrogate reasoning. This second feature requires that informed and competent agents be led to draw specific inferences regarding the target. These inferences can be the result of “any type of reasoning…as long as [the source] is the vehicle of the reasoning that leads an agent to draw inferences regarding [the target]” (2004, 773). Suárez’s point here is that not only does the source lead the agent to the target, but also it leads the agent to think about the target in a particular way, coming to particular insights and inferences with respect to the source.
More recently, Suárez (2010) has argued that this second feature, the capacity for surrogate reasoning, typically requires that three things be in place. First, the source must have internal structure such that certain relations between parts can be identified and examined. Secondly, when examining the parts of the source, scientists must do so in terms of the target’s parts. Finally, there must be a set of norms defined by the scientific practice which define and limit which inferences are “correct” or intended. It is in virtue of these norms of the practice that an agent will be able to draw the relevant and intended inferences, making the representation a part of that particular scientific practice. Of course, he takes his view to be deflationary, so these are not to be understood as necessary and sufficient conditions of the capacity for surrogate reasoning, but rather features which are frequently in place.
Consider an example of a mathematical model, for example the Lotka-Volterra equation. The model is supposed to be representational of predator-prey relationships. Part of this is Suárez’s representational force—the fact that competent agents will be lead to consider predator-prey relationships when considering the source. However, as Suárez notes, this is insufficient for scientific representation because in science the terms interact in a non-arbitrary way. To account for this, he argues that there is another feature of the model, which is the capacity to allow for surrogate reasoning. In this case, that means that individuals who examine or manipulate the model in terms of its parts (the multiple variables) will be able to draw certain inferences about the nature of real-world interactions between predators and prey (the parts of the target system). These insights will occur in part due to the nature of the model as well as the norms of scientific practice, which means that the inferences will be non-arbitrarily related to the real-world phenomena and will afford us to recognize certain specified inferences of scientific interest.
ii. Contessa
Suárez’s inferential account has been further developed by Gabriele Contessa (2007, 2011). He is explicit in his claim that the interpretational view he is defending is not a deflationary account, but is rather a substantive version of the inferential account insofar as he takes the account to give necessary and sufficient conditions of representation. All the same, the account he defends is clearly pragmatic in nature. Contessa begins by noting an important distinction he has drawn from Suárez’s work, that of the difference between three types of representation. The first is mere denotation, in which some (arbitrarily) chosen sign is taken to stand for some object. He gives the example of the logo of the London Underground denoting the actual system of trains and tracks.
The second sort of representation is what Contessa calls “epistemic representation” (2007, 52). An epistemic representation is one which allows surrogate reasoning of the sort described by Suárez. The London Underground logo does not have this feature since no one would be able to use it to figure out how to navigate. A map of the London Underground, on the other hand, would have this feature insofar as it could be used by an agent to draw these sorts of inferences.
The final sort of representation is what he calls “faithful epistemic representation” (2007, 54-55). Whether or not a representation is faithful is a matter of degree, so something will be a completely faithful epistemic representation provided all of the valid inferences which can be drawn about the target using the source as a vehicle will also be sound. Notice this does not require that a model user be able to draw every possible inference about the target, but rather that the inferences licensed by the map that are drawn will be sound inferences (both following from the source and true of the target). In this sense, a map of the London Underground produced yesterday will be more faithful than one produced in the 1930s.
Using this framework, Contessa goes on to describe a scientific model as an epistemic representation of features of particular target systems (56). The scientific model will be representational for a user when she interprets the source in terms of the target. He remains open to there being multiple sorts of interpretation which are relevant, but suggests that the most common sort of interpretation is “analytic,” which functions quite similarly to an isomorphism in which every part and relation of the source is interpreted as denoting one and only one part and relation in the target (and all of the target’s parts and relations are denoted by some part or relation from the source).
Of course, given that this is determined by the agent’s use, it is not necessary that the agent believe that her interpretation is actually the case about the system. Here is where Contessa draws on the distinction of faithfulness. Since models are often misrepresentations and idealizations as has been discussed above, they need not be completely faithful in order to be useful. This is not the end of the story, though, because the circumstances also play an important role in understanding whether or not something is a scientific representation.
c. Agent-Based Versions of Substantive Accounts
In light of some of the insights of Suárez and others, many of the views described above as substantive views were altered and updated to more explicitly and centrally make reference to the role of an agent, making them what could be called agent-centered approaches. Of most importance, given their role in the substantive views as described above are recent advances made by van Fraassen and Giere.
i. Agent-Based Isomorphism
The view of isomorphism commonly attributed to van Fraassen, which was described above, was the one drawn from his 1980 book, The Scientific Image. More recently, van Fraassen has presented an altered account of representation, which places much more emphasis on the role of an agent in his (2008). Van Fraassen notes that while some reference to an agent was a part of his earlier views (Ladyman, Bueno, Suárez, and van Fraassen, 2010), Suárez’s important work on deflationary accounts was influential in the development of the view he defends (2008, 7, 25-26; 2010).
He begins his account by looking primarily to the way in which a representation is used, saying that a source’s being representative of some target “depends largely, and sometimes only” on the way in which the source is being used (2008, 23). Though he does not take himself to be offering any substantive theory of representation, he does call this the Hauptsatz or primary claim of his account of representation: “There is no representation except in the sense that some things are used, made, or taken, to represent things thus and so” (2008, 23). Van Fraassen notices that this places some restrictions on what can possibly be representational. Mental images are limited, because they are not made or used in some way. That is to say, we do not give our mental states representational roles. Similarly, there is no such thing as a representation produced naturally. What it is to be a representation is to be taken or used as a representation, and this is not something that happens spontaneously without the influence of an agent.
Van Fraassen also notices an important distinction in two ways of representing: representation of and representation as. When scientists take or use some source to be representational, they take it to be a representation of some target. This target can change based on context, and sometimes scientists might not even use the source to be a representation at all. Consider van Fraassen’s example: we can use a graph to represent the growth of bacterial colonies under certain conditions, and so the graph will be a representation of bacterial growth (2008, 27). But we could also use that graph to represent other phenomena, perhaps the acceleration of an object as it is dropped from some height. Part of what this captures is the way in which our perspectives can change the way in which we are representing a particular appearance. Thus, by using a source in some distinct way, we can represent some particular appearance of some particular phenomena.
In intentionally using a source as a representation, scientists do not only make it a representation of something, but they also represent it in a certain light, making certain features salient. This is what van Fraassen calls representation as. Two representations can be of the same target, but might represent that target as something different. Van Fraassen offers an example: everything that has a heart also has a kidney, but representing some organism as having a heart does not mean the same thing as representing it as has having kidneys (2008, 27). Similarly, we might represent the growth of bacteria mentioned above as an example of a certain sort of growth model or as the worsening of some infection as it is seen as part of a disease process.
Of course, all of this is very general, which van Fraassen acknowledges. However, in a true deflationary attitude, he notices that there is no good way of getting more specific about scientific representation since it has “variable polyadicity: for every such specification we add there will be another one” (2008, 29). Nonetheless, he still maintains that the link between a good or useful representation and phenomena requires a similarity in structure. As it stands, then, there is still an appeal to isomorphism present in his account: “A model can (be used to) represent a given phenomenon accurately only if it has a substructure isomorphic to that phenomenon” (2008, 309). Just as before, we have an account of representation which relies on isomorphism between the structure of the theoretical models and the (structure of) the phenomena. All the same, this is still a markedly different view from his earlier view described above. No longer is it the isomorphism or structural relationship alone which is representational. Now, on van Fraassen’s views, it is the fact that a scientific community uses it or takes it to be representational.
ii. Agent-Based Similarity
Ian Hacking (1983) has famously argued that, in philosophical discussions of the role and activity of science, too much emphasis is put on representation. Instead, he suggests that much of what is done in science is intervening, and this concept of intervention is key to understanding the reality with which science is engaged. All the same, he still thinks that science can and does represent. Representation, on his account, is a human activity which exhibits itself in a number of different styles. It is people who make representations, and typically, they do so occurs in terms of a likeness, which he takes to be a basic concept. Representation in terms of likeness, he thinks, is essential to being human, and he even speculates that it may have played a role in development like many think language did. In creating a likeness, though, he argues that there is no analyzable relation being made. Instead, “[likeness] creates the terms in a relation…First there is representation, and then there is ‘real’” (139). Representation on his view is not interested in being true or false, since the representation precedes the real.
Giere (2004, 2010) has also made pragmatics more central and explicit to his account of scientific representation. He claims that in attempting to understand representation in science we should not begin with some independent two-place relationship, which substantially exists in the world. Instead, we should begin with the activity of representing. If we are going to view this activity as a relationship, it will have more than two places. He proposes a four-place relation: “S uses X to represent W for purposes P” (2004, 743). Here, S will be some agent broadly construed, such that it could be some individual scientist, or less specifically some group of scientists. X is any representational object, including models, graphs, words, photographs, computational models, and theories. W is some aspect or feature of the world and P are the aims and goals of the representational activity; that is, the reasons why the scientist is using the source to represent the target. Giere identifies a number of different potential purposes of representation. These include things like learning what something is actually like, but are fairly contextual and depend upon the question being asked. So the way in which something is modeled might change depending on the purposes of the representation (2004, 749-750).
Giere is still working from what should be considered a semantic conception of theories, in which a theory is a set of models which are created according to a set of principles and certain specific conditions. The principles are what we might otherwise think of as being empirical laws, but he does not conceive of them as having empirical truth. Instead, by thinking of them as principles by which scientists can form models, it is these scientists who construct and use the models who make particular the otherwise general and idealized principles. On this view, then, it is the models which are representational and will link up to the empirical world.
There are many ways a scientist can use a model to represent the world, on Giere’s view, but the most important way remains similarity. Giere is quick to note that this does not mean that we need to think of the representational relationship as some objective or substantive relationship in the world. Instead, the scientist who uses the model does the representing and she will often do this in virtue of picking out certain salient features of a model which are similar to the target system. In doing so, the scientist specifies the relevant aspects and degrees of similarity which she is using in her act of representation.
One of the advantages of this updated version of the similarity view is the wide range of models which can be effectively representational on this account (Giere 2010). Giere gives an example of a time when he saw a nuclear physicist treat a pencil as a model of a beam of protons, explaining how the beam could be polarized. It is in virtue of the invoked similarity between the pencil and a beam of photons, that is, the fact that the physicist specifically used a relevant similarity, that he was able to use it to represent the beam of photons. By noting the importance of the role of the agent, Giere is better able to explain the scientific representation which occurs in the whole range of scientific representations.
A similar yet importantly distinct account of representation as similarity is defended by Paul Teller (2001). Teller argues that we should abandon what he called the perfect model model, in which we take scientists to model in a way that is perfectly correspondent with the real world targets. Instead, he thinks that models are rarely, if ever, perfect matches for their targets. This does not mean that models are not representations. He argues that models represent their targets in virtue of similarity, though he denies that any general account of similarity can be given. What makes something a similarity depends deeply upon the circumstances at hand including the interests of the model user.
d. Gricean
One way to ‘deflate’ the problem of scientific representation is to claim that there is no special problem for scientific representation, and instead argue that we should understand the question of scientific representation as part of the already widely discussed literature on representation in general. This is the project taken up by Craig Callender and Jonathan Cohen (2006). According to their view, representation in many different fields (art, science, language, and so forth) can be explained by more fundamental representations, which are common to each of the fields.
To explain this, they appeal to what they call “General Griceanism”, which takes its general framework from the insights of Paul Grice. On their General Gricean view, the representational nature of scientific objects will be explained in terms of something more fundamentally representational. The more fundamentally representational objects in this case are mental states. This, in effect, pushes the hard philosophical problem back a stage, since some account must be given with regard to the representational nature of mental states. They remain uncommitted to any particular account of the representational nature of mental states, leaving that something to be argued about in philosophy of mind. All the same, they mention a few popular candidates: functional role theories, informational theories, and teleological theories.
There are, on their view, significant advantages to taking this General Gricean viewpoint. For one, it has a certain sort of simplicity to it. By explaining all representation in terms of the fundamental representations of mental states, we do not need to give wildly different explanations as to why a scientific model represents its target and why, for example, a green light represents ‘go’ to a driver. Each occurs because, in virtue of what the scientist or “hearer” knows, a certain mental state will be activated which contains with it the relevant representational content.
They can also explain the reasons why similarity or isomorphism will be commonly used (though non-necessary) since these are strong pragmatic tools in helping to better bring about the relevant mental state with its representational content. This is, as they argue, clearly one of the reasons why people from Michigan use an upturned left hand to help them explain the relative location of their hometown–because the upturned left hand is similar in shape to the shape of Michigan. The reasons why similarity is a useful tool here are identical to the reasons why similarity would be useful in scientific contexts, because it will make the relative instance of communication more effective–meaning that the hearer (or user of a model or scientific representation) will be better able to arrive at the relevant mental states which represent the target system.
In short, their view is that while there might be a general philosophical problem of representation, there is not anything special about scientific practice that makes its stake in this problem any different from any other field or the general problem. Of course, as they amusingly note, this passes the buck to the more fundamental question: “Once one has paid the admittedly hefty one-time fee of supplying a metaphysics of representation for mental states, further instances of representation become extremely cheap” (71).
e. Critiques of Deflationary and Pragmatic Accounts
These deflationary and pragmatic accounts of representation have not avoided criticisms of their own. Many of these criticisms are presented as part of the defense of one of the views over another. For example, Contessa (2011) argues against a purely denotational account of scientific representation, such as the one seen in Callendar and Cohen’s (2006). As he says, “Whereas denotation seems to be a necessary condition for epistemic representation, it does not, however, seem to be a sufficient condition” (2011, 125). As Contessa argues, it is insufficient merely to be able to stipulate a denotational relationship to have the sort of representation which is useful to scientists. For example, we might use any given equation (for example, F=ma) to denote the relationship which holds between the size of predator and prey populations. But, while this equation could successfully denote this relationship, it will not be of much use to scientists because they will not be able to draw many insights about the predator-prey relationship. Therefore, Contessa argues, while denotation is a necessary condition of representation, it cannot alone be the whole story. In addition, he suggests the need for interpretation in terms of the target, as described above.
Matthias Frisch (2015, 296-304) has raised a worry which he addressed specifically to van Fraassen’s (2008) account, but which is applicable to many of the pragmatic and deflationary accounts described above. The worry is that if we take van Fraassen’s Hauptsatz (“There is no representation except in the sense that some things are used, made, or taken, to represent things thus and so” (2008, 23)) literally, then it seems to be impossible that some models can represent. Taking Frisch’s example, say we wanted to construct a quantum mechanical model of a macroscopic body of water. To do this, “we would have to solve the Schrödinger equation for on the order of 1025 variables—something that is simply impossible to do in practice” (297). But if this is so, then it turns out that that the Schrödinger equation cannot be used to represent a macroscopic body of water—since we could never use the equation in this way, it is not representational in this way. Notice that this concern applies to other pragmatic and deflationary accounts: if we are unable to make inferences or interpret the source in terms of the target (which, given the complexity here, it seems we would not be able to do), then it will also fail to be representational on these other accounts. But this leads to a fairly strong conclusion that we can only use a model to represent a system once we have actually applied the model to that system. For example, the Lotka-Volterra model seems to only represent those systems for which scientists have used it; it does not represent all predator-prey relationships, in general.
Frisch (2015, 301-304) does not think that this argument is ultimately fatal to the pragmatic accounts since he argues that because there are constraints on the use of models which are part of the scientific practice, there is a sense in which the Lotka-Volterra model, for example, represents all predator-prey relationships (even though it has not yet been used in this way). There is no problem in extending models “horizontally,” that is, to other instances which are in the same domain of validity of the model. There is, Frisch argues, a problem in extending models “vertically,” that is, using a model to represent some phenomena which is outside the domain of validity. This can be seen in the quantum mechanics example from above since we do not have any practice in place to use Schrödinger equations to describe macroscopic bodies of water. So, he claims, van Fraassen’s view (and, by extension, the other pragmatic and deflationary views) must be committed to an anti-foundationalism (a view that the sciences cannot be reduced to one foundational theory) that denies that the models of quantum mechanics can adequately represent macroscopic phenomena. Of course, the anti-foundationalist commitments might be viewed as a desirable feature of these views, rather than a flaw, depending upon other commitments.
Another important critique which applies more generically to a number of these deflationary and pragmatic views comes from Chakravartty (2009). As described above, many of those who argue for a deflationary or pragmatic account of representation offer their view as an alternative to the substantive accounts. That is to say, they deny that scientific representation is adequately described by the substantive accounts and do not merely add to these accounts, but rather reject them and offer their deflationary or pragmatic account instead. Chakravartty argues that this is a mistaken move. We should not think of deflationary or pragmatic accounts as alternatives to the substantive accounts, but rather as compliments. On the deflationary or pragmatic accounts, representation occurs when inferences can be made about the target in virtue of the source. But, “how, one might wonder, could such practices be facilitated successfully, were it not for some sort of similarity between the representation and the thing it represents—is it a miracle?” (201). That is to say, the very function which proponents of the deflationary or pragmatic accounts take to be the central explainer of scientific representation seems to require some sort of similarity or isomorphism (Bueno and French 2011). On Chakravartty’s view, the pragmatic or deflationary accounts go too far in eliminating the role for some substantive feature. In doing so, they leave an important part of scientific representation behind.
3. Model-Based Representation
The question of scientific representation has received important attention in the context of scientific modeling. There is a vast literature on models, and much of it is at least tangentially related to the questions of representation. An examination of this literature provides an opportunity to see other sorts of insights with regard to representation and the relationship between the world and representational objects.
a. Models as Representations (and More)
Much of the literature on models focuses on the various roles of models within scientific practice, both representational and others. In an influential volume on models, Margaret Morrison and Mary Morgan (1999) use a number of examples of models to defend the view that models are partially independent from theories and data and function as instruments of scientific investigation. We can learn from models due to their representational features. Morrison and Morgan start out by focusing on the construction of models. Models, on their account, are constructed by combining and mixing a range of disparate elements. Some of the elements will be theoretical and some will be empirical, that is, from the data or phenomena. Thus far, this view is mostly in line with what has been discussed in the above sections. What makes models unique in their construction is that they often involve other outside elements. These can be stories (ways of explaining some unexpected data which are not part of a theory), other times it is a sort of structure which is imposed onto the data. These other elements, they argue, give models a sort of partial independence or autonomy. This is true even when the outside elements are not as obviously present, for example when a model is an idealized, simplified, or approximated version of a theory. This independence is crucial if we are to use them to help understand both theories and data as we often use them to do.
According to Morrison and Morgan, models function like tools or instruments for a number of purposes. There are three main classifications of the uses of models. The first is in interacting with theories: models can be used to explore a theory or to make usable a theory which is otherwise unusable. They can also be used to help understand and explore areas for which we do not yet have a theory. Other times, the models are themselves the objects of experimentation. The second classification of the use of models is in measurement: not only as a way of structuring and presenting measurements, but they can also function directly as instruments of measurement. Finally, models are useful when designing and creating technology.
Models are not valuable only insofar as they have these functions. Models, Morrison and Morgan argue, are also importantly representational. Their representational value relies in part on the way in which they are constructed with both the theory and the data or phenomena. Models can represent theories, data, or can be representational instruments which mediate between data and theory. Whatever the case, representation, on their view, is not taken to be some mirroring or direct correspondence between the model and its representational target. Instead, “a representation is seen as a kind of rendering–a partial representation that either abstracts from, or translates into another form, the real nature of the system or theory, or one that is capable of embodying on a portion of a system” (1999, 27). Sometimes models can be used to represent non-existent or otherwise inaccessible theories, as they claim is the case with simulations.
The final role of models described by Morrison and Morgan is the way that models afford the possibility of learning. Sometimes the learning comes in the construction of the model. Most frequently, though, we can learn using models by using and manipulating them. In doing so, we can learn because the models have the other features already described: the wide range of sources for construction, the functions, and their status as representations. Oftentimes, the learning takes place internal to the model. In these cases, the model serves as what they call a representative rather than a representation. With representatives, the insights we can gain from manipulating the model are all about the model itself. But in doing so, we come to a place from which we can better understand other systems, both real-world systems and other systems. Other times, we take the world into the model and then manipulate the world inside the model, as a sort of experiment.
Daniela Bailer-Jones (2003, 2009) defends a slightly different but related account of the representational nature of models. On her account, models entail certain propositions about the target of the model. As propositions, they are subject to being true or false. One way of thinking about the representation of models is to say that models are representational insofar as their entailed propositions are true. However, this cannot be exactly right, since, as was mentioned above, models oftentimes intentionally entail false propositions. Since models are about those aspects of a phenomenon which are selected, they will fail to say things about other aspects of a phenomenon. In some cases, the propositions entailed may be true for one aspect but false for another. This calls for the role of model users who decide what function the model has, the ways in which and degree to which the model can be inaccurate, and which aspects of the phenomenon are actually representing. In sum, on her view, models are representational in part due to their entailed propositions, but also due to the role of the model users.
Tarja Knuuttila (2005, 2011) has argued that in thinking about models too much emphasis has been placed on their representational features – even in accounting for their epistemic value. Following and expanding on Morrison and Morgan (1999), she argues that we should think of models as being material epistemic artefacts, that is, “intentionally constructed things that are materialized in some medium and used in our epistemic endeavors in a multitude of ways” (2005, 1266). The key to their epistemic functioning is to be found from their constrained and experimentable nature. Models, according to this account, are constrained by their construction in such a way that they make certain scientific problems more accessible, and amenable to a systematic treatment. This is one of the main roles of idealizations, simplifications, and approximations. On the other hand, the representational means used also impose their own constraints on modeling. The representational modes and media through which models are constructed (for example, diagrams, pictures, scale models, symbols, language) all afford and limit scientific reasoning in their different ways. When considered in this respect, Knuuttila argues, we can see that models have far more than mere representational capacities including that they are themselves the targets of experimentation and can be thought of as creating a sort of conceptual parallel reality.
b. Model-Building
In addressing model-building Weisberg (2007b) and Godfrey-Smith (2006) both take up the idea that the characteristic ways in which models are constructed is indirect. This comes about in a three step process in which a scientist first constructs a model, then analyzes and refines the model, and finally examines the relationship between the model and the world (Weisberg 2007b, 209). Models are used and understood by scientists with “construals” of the model (Godfrey-Smith 2006). The construal, on Weisberg’s account, is made of four parts. The first is an assignment which identifies various parts of the model to the phenomena being investigated. The second part of a construal is the scope, which tells us which aspects of the phenomena are being modeled. The final two parts of the construal are each fidelity criteria. One of these is the dynamical fidelity criteria, which identifies a sort of error tolerance of the predictions of the model. The other is the representational fidelity criteria, which give standards for understanding whether the model gives the right predictions for the right reasons, that is, whether or not the model is linking up to the causal structure which explains the aspects of the phenomenon being modeled.
This strategy of model-based science is contrasted with a different sort of strategy, what Weisberg calls abstract direct representation. Abstract direct representation is the strategy of science in which study of the world is unmediated by models. He gives the example of Mendelev’s development of the periodic table of elements. This process did not begin with a hypothetical abstract model which is refined and then used representationally (as Weisberg thinks the process of model-based science proceeds). Instead, this process starts with the phenomena and abstracts away to more general features. Such distinction between modelling and abstract direct representation underlines the possibility that not all scientific representations need to achieved in same ways.
There are some worries about Weisberg’s understanding of the process of model-making (Knuuttila and Loettgers, in press). Through a close examination of the development of the Lotka-Volterra model, Knuuttila and Loettgers argue that the process of model-building often begins with certain sorts of templates, or characteristic ways of modeling some phenomena, typically adopted from other fields. Such already familiar modeling methods and forms offer the modeler a sort of scaffolding upon which they can imagine and describe the target system. They also argue that another distinct feature of model-making is its outcome-orientation. That is, in developing a model, a scientist will typically do so with an eye to the anticipated insights or features of the target system that they wish to represent. Thus, on their view, the modeler pays close attention to the target system or empirical questions in all stages of the development of the model (not just at the end, as Weisberg suggests).
c. Idealization
One of the important discussions that has developed primarily in the literature on models concerns idealization. Weisberg (2007a) argues that there are three different kinds of idealization, which he generically describes as “the intentional introduction of distortion into scientific theories” (639). The first kind of idealization he calls Galilean idealization. This is the sort of idealization in which a theory or model is intentionally distorted so as to make the theory or model simpler, in order to render it computationally tractable. This sort of idealization occurs when scientists ignore certain features of a system or theory, not because they are playing no role in what actually happens, but rather because including them makes the application of the theory or model so complex that they cannot gain traction on the problem. By removing these complexities, scientists distort their model (because it lacks complexities which reflect the target). But after gaining some initial computational tractability, they can slowly reintroduce the complexities and thus remove the distortions.
The second type of idealization is what Weisberg calls minimalist idealization. In a minimalist idealization, the only features that are carried into the model or theory are those causal features which make a difference to the outcomes. So, if some feature of a target can be left behind without losing predictive power, a minimalist idealization will leave that feature behind. As an example, Weisberg notes that when explaining Boyle’s law, it is often assumed that there are no collisions between gas molecules. This is, in fact, false since collisions between gas molecules are known to take place in low-pressure gasses. But, “low pressure gases behave as if there were no collisions” (2007a, 643). So, since these collisions do not make any difference to our understanding of this system, scientists can (and do) leave this fact behind.
Notice that this is distinct from Galilean idealization insofar as minimalist idealizations leave certain features out of their theories or models because they make no difference to the relevant tasks or goals at hand. Galilean idealization, on the other hand, leaves certain features out even when they do make a difference, simply because leaving them in would make the model more complex and less tractable.
The final sort of idealization described by Weisberg is what he calls multiple-models idealization. This is the practice of using a number of different, often incompatible models to represent or understand some phenomenon. In this case, none of the models by itself is capable of accurately modeling the relevant target system. All the same, each of the models is good at representing certain features of the target system. Thus, by using not just a single model but rather this group of models, each of which is distorted, scientists can get a better sense of the target system. Weisberg offers a helpful example: the National Weather Service uses a number of different models in making its weather forecasts. Each of the models used represents the target in a different way, each being inaccurate in some way or another. It is the use of all of these models that permits forecasts of higher accuracy since attempts to make a single model have resulted in less accurate predictions.
4. Sociology of Science
a. Representation and Scientific Practice
Many important insights on the nature of scientific representation have come not from the philosophy of science but rather from thinkers who would typically be considered part of the field of sociology of science. The insights from this field can serve as both a source of insight on the nature of representation in scientific practice, as well as a challenge to the primarily epistemically-oriented insights from the philosophy of science. Michael Lynch and Steve Woolgar (1990) edited an important collection of papers on scientific representation in practice written from the perspective of sociology of science called Representation in Scientific Practice. More recently, (2014), Lynch and Woolgar edited another collection with Catelijne Coopmans and Janet Vertesi. Treating representation from the perspective of sociology of science involves asking a different sort of question than the one so far addressed in this article. Instead of asking about the constitution of scientific representation, sociologists of science are more interested in a different question, “What do the participants, in this case, treat as representation?” (Lynch and Woolgar 1990, 11). In the introduction to this volume, Lynch and Woolgar provide a general overview of some of the important insights from this perspective.
Since sociology of science treats scientific practice as its object of inquiry, it is keen to describe precisely how representations are actually used by scientists. They note the importance of “the heterogeneity of representational order” (2). That is, there is a wide range of devices which are representational as well as a wide range of ways in which the representations are used and in which they are useful. Importantly, sociologists are often interested in discussing more than merely the epistemic or informational role and use of representations, viewing them as significantly social, contextualized, and otherwise embedded in a complex set of activities and practices. Sociologists of science attempt to pay attention to the whole gamut of representations and representational uses to better understand precisely the role they play within scientific investigation.
Another important insight, Lynch and Woolgar note, is that the relation between representations is not to be thought of as directional in the sense that the representations move from or towards some “originary reality” (8). Instead, any directionality of representations is to be thought of as “movement of an assembly line” (8). That is to say, representational practice must be seen as constructing not only a representation, but also (re)constructing a phenomenon in a way so that it can be represented. This is something that can be seen in much of the literature from sociologists of science, including the work of Latour (see below).
In paying close attention to the way representations are actually used, some sociologists of science note settings in which “discrepancies between representations of practice and the practices using (and composing) such representations” (9). These discrepancies and other problems encountered in the actual practice of science allow for improvisation and creativity which can help advance the particular domains of which they are a part. Sociologists of science are interested in studying this creativity, not only for its productivity in science, but also as an interesting phenomenon in its own right.
b. Circulating Reference
A particularly telling example of these insights, especially from the philosophical point of view, is provided in Bruno Latour’s “Circulating Reference” (Latour 1999). Latour’s photo-philosophical case study is based on the work of a group of scientists who were examining the relationship between a savannah and forest ecosystem. At the end of their project, they collectively published a paper on their findings which included a figure of the interaction between the ecosystems, detailing the change in soil composition among other features. Latour asks how it is that this abstract drawing, which takes a perspective no individual could possibly have had and which ignores so many of the features of the ecosystem, can be about that stretch of land. That is to say, here we have a drawing, something made by ink and paper, and there we have the forest-savannah ecosystem, how is it that the former can be about the latter?
Latour’s method of answer, which takes the form of a strikingly well-written case study in which he presents pictures from the expedition which he uses to structure and represent the process he describes, is to look carefully at all the details and steps by which the scientists got from the expedition to the figure in the paper. What happens, says Latour, is that there are a series of steps through which the scientists abstract from the world in some intentional fashion. In doing so, they maintain some relevant feature of the world, but they are simultaneously constructing the phenomena they are studying. In the process the representations produced are also getting more abstract.
An example will make this clearer. At one stage in the process, soil samples are collected from a vertical stretch of ground. These samples are transferred into a device which allows the whole vertical stretch of earth to be viewed synoptically. In taking the sample, the scientist has already begun to construct–already this particular bit of dirt is taken to be representative of the dirt for a much wider area of land. Once the soil has been collected, various features of the soil are maintained through intentional actions on the part of the scientist. For example, the scientists will label the soil as being of a certain sort of consistency. The scientists then use a clever device in which there are pinholes in a tool which has the various Munsell colors and numbers, which is itself a construction with a long history. In looking through the pinholes, the scientist can abstract away from the dirt sample itself, taking, in some sense, only the color (which is done in virtue of a construction of numbers associated with particular colors). Something has clearly been lost, namely, the full materiality of the dirt. But something has also been gained, in this case, a number which corresponds to the color of the dirt; some usable, manipulable data.
Latour’s essay carefully describes many of these transitions from the savannah-forest system to the published figure. As he claims, it is this series of transitions (which each involve abstraction and construction due to the intentional decisions of a scientist) which ensures that the figure at the end references or represents the savannah-forest system. There is not a single gap between the figure and the world which must be accounted for by some representational relation. Instead, on his account, there is a large series of gaps, each of which is crossed by a scientist’s actions in abstracting and maintaining, constructing and discovering. This series, he thinks, can be extended infinitely in either direction. By abstracting further from the already quite-abstract figure, certain hypotheses might be suggested, which would result in a return to the savannah-forest system, to gather data which might be more basic than the data already gathered. On his view, there is no such thing as “the world” which is the most basic thing-in-itself. Nor is there any most-abstracted element.
c. Critiques of Sociology of Science
While these insights from the sociology of science literature have been both sources of support and criticism for the philosophical literature, they have also been subject to criticisms. One important criticism comes from Giere’s (1994) review of Lynch and Woolgar’s (1990) Representation in Scientific Practice. Giere’s primary target is the extremely constructivist nature of the sociology of science literature. The constructivist approach claims that science is socially constructed: that is, science is filled with socially-dependent knowledge and aimed at understanding socially-constructed objects. There is no such thing, on this view, as a non-constructed world to be understood by scientists, and therefore, no such world to be represented. The attempt to explain representation in this framework results in a “no representation theory of representation” (Giere 1994, 115). But, Giere thinks there is a straightforward counter-slogan to a view of this sort: “no representation without representation” (115). That is to say that if there is nothing ‘out there’ in the world being represented, it cannot be that this is an instance of representation. This is not to reject the importance of paying attention to the role of the practices and representational devices in particular case studies. All the same, Giere argues that if we want a general account of scientific representation, “we must also go beyond the historical cases” (119). Put otherwise, the sociology of science perspective is an important part of explaining scientific representation, but this work by itself leaves representation unexplained.
Knuuttila (2014) takes up a similar line of criticism. While she places great importance on the insights of sociologists of science, she thinks that many of their views have developed with a false target in mind. Many sociologists of science place their views as a contrast to a traditional philosophical view of science as something which perfectly represents the world. The alternative, they suggest, is their constructivist approach, as described above. However, Knuuttila argues, this motivation runs into problems. First, when they select certain practices to investigate rather than others, by what criterion are they distinguishing this practice as representational? In doing so, they seem to be relying on some traditional account of representation to delineate the cases of interest. Further, it seems that these studies do not show that representation is a defunct concept and that we are bound to a purely constructivist account of science. Instead, “these cases actually reveal…what a complicated phenomenon scientific representation is…and give us clues as to how, through the laborious art of representing, scientists are seeking and gaining new knowledge” (Knuuttila 2014, 304). We need not think that just because there is no perfect representation of the world, that there is therefore no world to be represented. Their insights could equally contribute to an intermediate view in which we reject this perfect-representation view of science, but still maintain that science is giving us knowledge of the real world. That is, we can simultaneously deny that representations “are some kind of transparent imprints of reality with a single determinable relationship to their targets” while still affirming that the “artificial features of scientific representations…result from well-motivated epistemic strategies that in fact enable scientists to know more about their objects” (Knuuttila 2014, 304).
5. References and Further Reading
- Bailer-Jones, D. (2003). When Scientific Models Represent. International Studies in the Philosophy of Science 17: 59-74.
- Representation in models is linked to entailed propositions and pragmatics.
- Bailer-Jones, D. (2009). Scientific Models in Philosophy of Science. Pittsburgh: University of Pittsburgh Press.
- Extended discussion of the history of philosophy of models and defends an account of models.
- Bartels, A. (2006). Defending the Structural Concept of Representation. Theoria 55: 7-19.
- Homomorphism as an account of representation.
- Brading, K. and E. Landry. (2006). Scientific Structuralism: Presentation and Representation. Philosophy of Science 73: 571-581.
- Structuralism as a strong methodological approach in science.
- Bueno, O. (1997). Empirical Adequacy: A Partial Structures Approach. Studies in History and Philosophy of Science 28: 585-610.
- Representation as partial isomorphism.
- Bueno, O. and S. French. (2011). How Theories Represent. British Journal for the Philosophy of Science 62: 857-894.
- Representation as partial isomorphism; replies to arguments against partial isomorphism.
- Callender, C. and C. Cohen. (2006). There Is No Special Problem About Scientific Representation. Theoria 21: 67-85.
- Scientific representation is to be explained like other problems of representation.
- Cartwright, N. (1983). How the Laws of Physics Lie. New York: Oxford University Press.
- Distortion and idealization in the laws of physics.
- Cartwright, N., T. Shomar, and M. Suárez. (1995). The Tool Box of Science: Tools for the Building of Models with a Superconductivity Example. Poznan Studies in the Philosophy of the Sciences and the Humanities 44: 137-149.
- Models are not only theory-driven, but also phenomena-driven.
- Chakravartty, A. (2009). Informational versus Function Theories of Scientific Representation. Synthese 72:197-213.
- Argues that substantive and pragmatic accounts are complementary.
- Contessa, Gabriele. (2007). Scientific Representation, Interpretation, and Surrogative Reasoning. Philosophy of Science 74: 48-68.
- A substantive inferential account of representation.
- Contessa, Gabriele. (2011). Scientific Models and Representation. In S. French and J. Saatsi (eds.) The Bloomsbury Companion to the Philosophy of Science, pp. 120-137. New York: Bloomsbury Academic.
- A substantive inferential account of representation.
- Coopmans, C. J. Vertesi, M. Lynch, S. Woolgar (eds.). (2014) Representation in Scientific Practice Revisited. Cambridge: MIT Press.
- Reexamines the question of representation in scientific practice in contemporary sociology of science.
- da Costa, N. and S. French. (2003). Science and Partial Truth: A Unitary Approach to Models and Scientific Reasoning. Oxford: Oxford University Press.
- Representation as partial isomorphism.
- French, S. (2003). A Model-Theoretic Account of Representation (Or, I Don’t Know Much about Art… but I Know It Involves Isomorphism). Philosophy of Science 70: 1472-1483.
- Representation as partial isomorphism.
- French, S. and J. Ladyman. (1999). Reinflating the Semantic Approach. International Studies in the Philosophy of Science 13: 103-119.
- Representation as partial isomorphism.
- Frigg, R. (2006). Scientific Representation and the Semantic View of Theories. Theoria 55: 49-65.
- Criticisms of the semantic approaches to representation.
- Frisch, M. (2015). Users, Structures, and Representation. British Journal for the Philosophy of Science 66: 285-306.
- Discusses van Fraassen’s (2008); presents and responds to a criticism.
- Giere, R. (1988). Explaining Science: A Cognitive Approach. Chicago: University of Chicago Press.
- A semantic account of theories and representation as similarity.
- Giere, R. (1994). No Representation without Representation. Biology and Philosophy 9: 113-120.
- Argues that an appeal only to practice will leave scientific representation unexplained.
- Giere, R. (2004). How Models Are Used to Represent Reality. Philosophy of Science 71: 742-752.
- Representation as similarity with input of agents.
- Giere, R. (2010). An Agent-Based Conception of Models and Scientific Representation. Synthese 172: 269-281.
- Representation as similarity with input of agents.
- Godfrey-Smith, P. (2006). The Strategy of Model-Based Science. Biology and Philosophy 21: 725-740.
- Discusses the use of models as being classified by a particular strategy in science.
- Goodman, N. (1976). Languages of Art. Indianapolis: Hackett.
- Argues for an account of representation in art which has been influential to accounts of scientific representation.
- Hacking, I. (1983). Representing and Intervening. New York: Cambridge University Press.
- Representation in terms of likeness, argues for the importance of intervention.
- Hesse, M. (1966). Models and Analogies in Science. Notre Dame, Indiana: University of Notre Dame Press.
- Argues that models are central to scientific practice.
- Hughes, R.I.G. (1997). Models and Representation. Philosophy of Science 64: S325-S336.
- The DDI account of representation.
- Knuuttila, T. (2005). Models, Representation, and Mediation. Philosophy of Science 72: 1260-1271.
- Models as epistemic tools.
- Knuuttila, T. (2011). Modelling and Representing: An Artefactual Approach to Model-Based Representation. Studies in the History and Philosophy of Science 42: 262-271.
- Relates representation to representationalism, and expands the notion of models as epistemic tools.
- Knuuttila, T. (2014). Reflexivity, Representation, and the Possibility of Constructivist Realism., In M. C. Galavotti, S. Hartmann, M. Weber, W. Gonzalez, D. Dieks, and T. Uebel (eds.) New Directions in the Philosophy of Science, pp. 297-312. Dordrecht, Netherlands: Springer.
- Criticizes sociology of science accounts and argues that they are compatible with philosophical accounts.
- Knuuttila, T. and A. Loettgers, A. (in press). Modelling as Indirect Representation? The Lotka-Volterra Model Model Revisited. British Journal for the Philosophy of Science.
- Focuses on the interdisciplinary, historical and empirical aspects of model construction.
- Latour, B. (1999). Circulating Reference. In Pandora’s Hope. Cambridge: Harvard University Press.
- Traces and discusses the steps from some phenomena to a representation.
- Ladyman, J., O. Bueno, M. Suárez, B.C. van Fraassen. (2011). Scientific Representation: A Long Journey from Pragmatics to Pragmatics. Metascience 20: 417-442.
- Discussion of van Fraassen’s (2008), with replies by van Fraassen.
- Lynch, M. and S. Woolgar (eds.). (1990). Representation in Scientific Practice. Cambridge: MIT Press.
- Collection of essays on scientific representation by sociologists of science.
- Morgan, M. and M. Morrison (eds.). (1999). Models as Mediators: Perspectives on Natural and Social Science. New York: Cambridge University Press.
- Collection of essays on the uses and nature of models.
- Suárez, M. (2003). Scientific Representation: Against Similarity and Isomorphism. International Studies in the Philosophy of Science 17: 225-244.
- Criticisms of similarity and isomorphism.
- Suárez, M. (2004). An Inferential Conception of Scientific Representation. Philosophy of Science 71: 767-779.
- Inferential account of representation.
- Suárez, M. (2010). Scientific Representation. Philosophy Compass 5: 91-101.
- Gives a brief overview of accounts of representation.
- Suárez, M. (2015). Deflationary Representation, Inference, and Practice. Studies in History and Philosophy of Science 49: 36-47.
- Discusses deflationary accounts and argues that both his inferential account and the DDI account are deflationary.
- Suppe, F. (1974). The Structure of Scientific Theories. Urbana: University of Illinois Press.
- Criticizes the syntactic view and introduces a semantic conception of theories.
- Teller, P. (2001). Twilight of the Perfect Model Model. Erkenntnis 55: 393-415.
- Argues for a deflationary account of similarity as representation.
- Toon, A. (2012). Similarity and Scientific Representation. International Studies in the Philosophy of Science 26: 241-257.
- Explores responses to criticisms on behalf of similarity.
- van Fraassen, B. C. (1980). The Scientific Image. New York: Oxford University Press.
- Representation as isomorphism (among other things).
- van Fraassen, B. C. (2008). Scientific Representation: Paradoxes of Perspective. New York: Oxford University Press.
- Representation as isomorphism with important role for agents (among other things).
- Weisberg, M. (2007a). Three Kinds of Idealization. Journal of Philosophy 104: 639-659.
- Three different sorts of idealization.
- Weisberg, M. (2007b). Who Is a Modeler? British Journal for the Philosophy of Science 58: 207-233.
- Models are indirect representations, a strategy which is distinct from abstract direct representation.
- Weisberg, M. (2013). Simulation and Similarity: Using Models to Understand the World. New York: Oxford University Press.
- Representation as similarity.
- Winther, R. (2015). The Structure of Scientific Theories. In E.N. Zalta (ed.), Stanford Encyclopedia of Philosophy. (Spring 2015 Edition). http://plato.stanford.edu/
- Detailed discussion of accounts of the structure and representation of scientific theories with extensive bibliography.
Author Information
Brandon Boesch
Email: boeschb@email.sc.edu
University of South Carolina
U. S. A.