Haskell Brooks Curry (1900-1982)
 Haskell Brooks Curry was a mathematical logician who developed a distinct philosophy of mathematics. Most of his work was technical: he was the major developer of combinatory logic, which nowadays plays a role in theoretical computer science. This formalism was originally intended to be a basis for a system of symbolic logic in the usual sense, but the original system turned out to be inconsistent, and the core which was consistent later became a formalism that is a kind of prototype of the computer languages called functional, in which programs are allowed to apply to and change other programs. It is essentially equivalent to the lambda-calculus (λ-calculus) of Alonzo Church. (See the article on λ-calculi in this encyclopedia.)
Haskell Brooks Curry was a mathematical logician who developed a distinct philosophy of mathematics. Most of his work was technical: he was the major developer of combinatory logic, which nowadays plays a role in theoretical computer science. This formalism was originally intended to be a basis for a system of symbolic logic in the usual sense, but the original system turned out to be inconsistent, and the core which was consistent later became a formalism that is a kind of prototype of the computer languages called functional, in which programs are allowed to apply to and change other programs. It is essentially equivalent to the lambda-calculus (λ-calculus) of Alonzo Church. (See the article on λ-calculi in this encyclopedia.)
Curry’s work on combinatory logic led him to a notion of formal system which is different in some respects from the one which has since become standard. In addition, Curry became interested in proof theory, especially the work of Gerhard Gentzen. Curry wanted to use these ideas in his search for a consistent system of logic based on combinatory logic. Curry also did some work on computing in the early days, including work on the ENIAC (one of the first electronic computers) immediately after World War II. Finally, he also became known for a philosophy of mathematics that he called formalism, which he originally considered as denying mathematics as the science of formal systems (in his sense), but which he later extended to include formal methods in general. This idea of formalism is probably better thought of today as a form of structuralism.
Table of Contents
- Biography
- Combinatory Logic
- Gentzen-style Proof Theory
- War Work and Computing
- Formalism: the Philosophy of Mathematics
- References and Further Reading
1. Biography
Haskell Brooks Curry was born on September 12, 1900 at Millis, Massachusetts. His father was Samuel Silas Curry, president of the School of Expression of Boston, Massachusetts. The School of Expression was originally founded by Anna Baright in 1879 as the School of Elocution and Expression. It was renamed in 1885, after Anna Baright married Samuel Silas Curry. It became Curry College in 1943. His mother was Anna Baright, who was Dean of the School of Expression. He graduated from high school in 1916 and entered Harvard University with the intention of going into medicine. During his first year, he took a mathematics course at the suggestion of his advisor and did very well. In the Spring of 1917, the United States entered World War I, and Curry responded by enlisting in the army, becoming a member of the Student Army Training Corps on October 18, 1918. He felt he would never play a direct role in the war if he continued with his pre-medical course, so he changed his major to mathematics with the idea of going into the artillery. The war ended on November 11, 1918, and Curry left the army on December 9, 1918, but he kept on in mathematics, receiving his A. B. degree in 1920.
For the next two years he studied electrical engineering at MIT in a program that involved working half-time at the General Electric Company. Because he was usually interested in why an answer was correct when the engineers seemed interested only in the fact that it was correct, he decided that he would be better off pursuing a degree in pure science, and in 1922 he switched to physics. He returned to Harvard, where for the year 1922–23 he was a half-time research assistant to P. W. Bridgman, who later won the Nobel prize in physics. In 1924 he received his A.M. in physics (from Harvard). But by this time his interests had shifted still further, and he now switched to mathematics. (During this period, both of his parents died, his father dying in 1921 and his mother in 1924.)
He continued to study mathematics at Harvard until 1927, where he was a half-time instructor during the first semester of 1926-27 but otherwise studied full-time. He was also involved in the business affairs of his family, the School of Expression.
During this period, Curry had become interested in logic. Originally, all of his logic was reading on the side, and at one point he was supposed to be working on a dissertation on a topic in differential equations assigned to him by George D. Birkhoff. Furthermore, he was getting advice from various faculty members at Harvard and elsewhere to stay away from logic. This advice was especially strong from Norbert Wiener, who was at MIT and who was a member of the same birdwatching club as Curry. But Curry had become too interested in logic to stop thinking about it. He was especially interested in the first chapter of Principia Mathematica [Russell and Whitehead 1910-1913], which he started reading in 1922 when he was 21 years old, and where a system of propositional logic is defined by means of axioms and two primitive rules. The first one is detachment, which says that from not-![]() or
or ![]() and from
and from ![]() to deduce
to deduce ![]() (this is equivalent to modus ponens, which says that from
(this is equivalent to modus ponens, which says that from ![]() and
and ![]() to deduce
to deduce ![]() ). The second one is substitution, which says that given any formula, any formula obtained by substituting another formula for a variable can be deduced; for example, if from the formula
). The second one is substitution, which says that given any formula, any formula obtained by substituting another formula for a variable can be deduced; for example, if from the formula ![]() , one can substitute
, one can substitute ![]() for
for ![]() to get
to get ![]() . Curry noticed when he first saw this that the rule of substitution is much more complicated than detachment in the sense that today we would find it more complicated to implement in a computer language. In 1926-27, as a result of trying to analyze substitution down to its simplest elements, Curry had the idea for using operators which he called combinators, the term we still use today. He used these operators to analyze this rule of substitution, and he concluded that this idea might lead to a dissertation. When he took this idea to several professors, he got a different reaction than he had previously had about staying away from logic. This was especially true of Norbert Wiener at MIT, who said that his opinion had been that logic was a subject to be avoided “unless you had something to say,” and since Curry clearly had something to say, “strength to your right arm!”
. Curry noticed when he first saw this that the rule of substitution is much more complicated than detachment in the sense that today we would find it more complicated to implement in a computer language. In 1926-27, as a result of trying to analyze substitution down to its simplest elements, Curry had the idea for using operators which he called combinators, the term we still use today. He used these operators to analyze this rule of substitution, and he concluded that this idea might lead to a dissertation. When he took this idea to several professors, he got a different reaction than he had previously had about staying away from logic. This was especially true of Norbert Wiener at MIT, who said that his opinion had been that logic was a subject to be avoided “unless you had something to say,” and since Curry clearly had something to say, “strength to your right arm!”
However, there was no faculty member at Harvard who could supervise a dissertation on this topic. So Curry decided that it would be useful to teach for a year, and, after getting a recommendation for the position from George D. Birkhoff, assumed an instructorship at Princeton for the year 1927-28. During a library search there he found the paper by Moses Schönfinkel, [Schönfinkel 1924], a report of a talk given at Göttingen in 1920, which had clearly anticipated his ideas. Curry was shocked at this anticipation because he had thought his ideas were completely original, and he ran to the office of Oswald Veblen, who, although primarily a geometer, was interested in the foundations of mathematics and who was also the PhD supervisor of Alonzo Church, to tell him about the anticipation. Veblen calmed Curry down by saying, “Good, I am always glad when somebody has one of my ideas, for it shows that I am on the right track.” To find out more about Schönfinkel, Veblen then took Curry to see the Russian topologist Pavel Alexandroff, who was visiting Princeton that year. Alexandroff reported that Schönfinkel was in a mental hospital and was unlikely to resume his mathematical work, but that at Göttingen were several mathematicians, including Paul Bernays, who were probably betteer paced to discuss these topics. It was thus decided that Curry should go to Germany.
As part of an application for financial support for that trip, Curry wrote his first published paper, [Curry 1929]. Before leaving for Germany, Curry married, on July 3, 1928, Mary Virginia Wheatley of Hurlock, Maryland. (Virginia had been a student at the School for Expression, where they met.) After the wedding, the Currys left for Germany, where they spent the year 1928-29 at Göttingen. During that year, Curry first met the logician Alonzo Church, who was there for half the year.
That year at Göttingen was enough for Curry to complete his dissertation. His referee was David Hilbert, although he actually did most of his work with Paul Bernays, and he was examined on July 24, 1929. At this examination, Hilbert asked Curry a question on another topic (called automorphic functions), which Hilbert assumed that Curry would not know. As it happened, Curry had taken a course on that very subject at Harvard, and Curry was able to give a good answer. Hilbert responded by asking in great surprise, “Wo haben sie das gelernt?” (“Where did you learn that?”) The dissertation was published (in German) as [Curry 1930].
Curry now needed a job, and he took up a position as an Assistant Professor at the Pennsylvania State College (Penn State – Penn State became the Pennsylvania State University in 1953). Eventually, most people who knew Curry came to associate him with Penn State, but when he first went there he did not plan to stay long. He had been at Harvard, Princeton, and Göttingen, and at Penn State he felt cut off from most of his former academic community. Furthermore, in those days, Penn State did not support research. (Later, thanks partly to Curry’s influence, Penn State changed its policy, and it is now a major research institution.) But his arrival there coincided with the beginning of the great depression, and the demand for logicians in the academic world was not very high. So he remained and settled down at Penn State, staying there, with the exception of several leaves of absence, until his retirement in 1966. He progressed normally through the academic ranks, becoming an Associate Professor in 1933 and a full Professor in 1941.
Everybody who knew the Currys was aware of how friendly and helpful they always were. Curry always did more for colleagues and students than be a source of important ideas (although, of course, his ideas have been of tremendous importance). He was always willing to listen to anybody who wanted to talk to him, to discuss their ideas, and to give whatever encouragement he could. His office door was always open. Also well known wherever the Currys lived was the hospitality they both showed. There were always many parties and other, less formal, gatherings. Curry also had a playful sense of humor.
The first of his leaves of absence was a year at the University of Chicago in 1931-32 as a National Research Council Fellow. (The original award was supposed to extend into the following year, but the second year was cancelled for Curry because he had a job to go back to and there were other National Research Council Fellows who did not. It was, after all, the depths of the Great Depression.) In 1938-39, Curry was in residence at the Institute for Advanced Study in Princeton.
Otherwise, Curry spent the 1930s at Penn State teaching and carrying on his research. During this period he was on the reviewing staff of the Zentralblatt für Mathematik und ihre Grenzgebiete (1931-1939). In 1936, he became a founding member of the Association for Symbolic Logic; he was Vice President in 1936-37 and President in 1938-40 as well as being a member of the Council as ex-president during 1942-46.
During this period, the Currys also began their family: Anne Wright Curry (later Mrs. Richard S. Piper) was born on July 27, 1930, and Robert Wheatley Curry followed on July 6, 1934.
By the end of the 1930s, Curry was established as one of the most important mathematical logicians in the United States and, in fact, in the entire world. As such, he was asked to present his views on the nature of mathematics to the International Congress for the Unity of Science held at Cambridge, Massachusetts at the beginning of September 1939. The result was a long manuscript of which he presented a shorter version to the Congress, [Curry 1939]. A series of papers on the philosophy of mathematics began with this paper and continued for the rest of his life.
In the following year, 1940, Curry became a member of the Board of Trustees of Curry College, formerly the School of Expression, the institution of which his father had been president. He remained a member until 1951. Later, on June 5, 1966, the college presented him with the honorary degree of Doctor of Science in Oratory.
When the United States entered World War II, Curry decided to put logic aside for the duration of the war. From 1940 until 1942 he had been a member of the National Committee on War Preparedness of the American Mathematical Society and the Mathematical Association of America. On May 25, 1942, he left Penn State and went to the Frankford Arsenal, where he worked as an applied mathematician until January 1944; then he went to the Applied Physics Laboratory at Johns Hopkins University, where he remained until March, 1945. Next he went to the Ballistic Research Laboratories at the Aberdeen Proving Ground, where he stayed until September, 1946. During his last three months there, he was Chief of the Theory Section of the Computing Laboratory and for one month he was Acting Chief of the Computing Laboratory; it was during this period that he became involved with the ENIAC computer. As a result of this experience he was a consultant in the field of computing methods to the United States Naval Ordinance Laboratory from June 1, 1948 until June 30, 1949.
In September, 1946, Curry returned to Penn State. He wanted to pursue his work on electronic computers, and so he tried to interest the university in acquiring some computing equipment. He was unsuccessful in this. He persisted until a colleague pointed out to him that if he did succeed, he would probably be made head of the program without any increase in salary. He then decided that this colleague was right and gave up the attempt. This effectively limited him from pursuing computing theory.
He was, however, getting back to logic. In Amsterdam in the summer of 1948, during the Tenth International Congress of Philosophy, it was proposed to him that he write a little book of under 100 pages on the subject of combinatory logic for the new North-Holland series in logic. He felt that there was too much unpublished research on the subject to write such a short book, and so he sent them instead his philosophical manuscript from 1939 with a few minor revisions. This appeared as [Curry 1951]. But this idea did suggest to him the project that eventually led to his two volumes with the title Combinatory Logic [Curry and Feys 1958] and [Curry et al.1972]. Feeling that he needed a collaborator, especially one who was better than he was at exposition, he decided to work with Robert Feys, who had published some papers on combinatory logic. Curry thus obtained a Fullbright grant and spent the year 1950-51 at Louvain in Belgium. After his return to Penn State, he and Feys continued their work, and the manuscript of [Curry and Feys 1958] was completed in 1956. The book appeared in 1958, published by North-Holland.
Meanwhile, money finally became available at Penn State for graduate students. Edward J. Cogan first approached Curry before he left for Louvain, and worked with Curry after he returned in 1951, finishing his dissertation in 1955. Kenneth L. Loewen also studied with him during this period, but left to take an academic position elsewhere in 1954 and did not finish his dissertation until 1962.
After the completion of [Curry and Feys 1958] Curry turned his attention to Gentzen-style proof theory. He had done some previous work on this, including a series of lectures delivered at Notre Dame University in Indiana in April, 1948 (which resulted in his book [Curry 1950]), and he felt that it formalized the kind of reasoning used in the development of the part of combinatory logic as a system of logic in the usual sense, and so he felt that it should be settled before he began work on [Curry et al. 1972]. He thus began work on what became his book [Curry 1963]. This work was made easier when, in 1959, he became Evan Pugh Research Professor and was thus relieved of undergraduate teaching duties. The manuscript of [Curry 1963] was completed in 1961.
By this time, there were two more graduate students, Bruce Lercher and Luis E. Sanchis, both of whom completed their dissertations in 1963.
From February to September, 1962, the Currys took a trip around the world, visiting a number of universities where Curry gave lectures.
In 1964, Curry met two new future collaborators. J. Roger Hindley arrived at Penn State for a lectureship which served as something of a postdoctoral position after finishing his dessertation at Newcastle-upon-Tyne, and Jonathan P. Seldin arrived as a beginning graduate student. Curry was just beginning work on [Curry et al. 1972]. Unfortunately, Feys had died in 1961, and Curry, left to work alone, soon realized that he needed collaborators. In 1965, he invited Hindley to join him on the project.
In 1966, Curry retired from Penn State after being there for 37 years. He then went to Amsterdam, where for the next four years he was Professor of Logic, History of Logic, and Philosophy of Science, and also Director of the Instituut voor Grondslagenonderzoek en Philosophie der Exacte Wetenschappen, both at the university of Amsterdam. Seldin went to Amsterdam on a Graduate Fellowship from the United States National Science Foundation, and completed his dissertation in 1968, after which he joined Curry and Hindley as a co-author of the book they were then writing. Curry had one more graduate student in Amsterdam, Martin W. Bunder, who finished his dissertation in 1969.
The manuscript of [Curry et al. 1972], was completed in May, 1970, just before Curry retired from the University of Amsterdam. He returned to State College, Pennsylvania (the town in which Penn State is located), where he continued his mathematical work, writing reviews (especially for Mathematical Reviews) and occasional papers. John A. Lever wrote a master’s thesis with him there in 1977 after obtaining special permission from the university authorities to work under a retired professor. In 1971-72, Curry accepted a visiting position at the University of Pittsburgh. Otherwise, he and Virginia remained at State College, except for some occasional trips, until his death on September 1, 1982. Curry left his papers to the library at Penn State.
Curry’s hobby throughout his life was bird watching, and by the end of his life, Curry had a reputation as an amateur ornithologist.
2. Combinatory Logic
a. Beginning Period
Curry invented combinatory logic independently by analyzing the operation of the substitution of a well-formed formula for a propositional variable in the system of propositional logic of the first chapter of [Russell and Whitehead 1910-1913]. He intended combinatory logic to be a foundation for mathematical logic and perhaps also for all of mathematics. Much of the subject is extremely technical. This will be as non-technical an introduction as it is possible to write.
The basic idea here is that of a function, which is a mathematical operation which does something to an input. Thus, for example, there is the numerical function which squares its argument (i.e., multiplies it by itself). Mathematicians usually write that if ![]() is the squaring function, then for each possible argument (input)
is the squaring function, then for each possible argument (input) ![]() ,
, ![]() . Then, if this function is applied to the number 3, we get
. Then, if this function is applied to the number 3, we get ![]() .
.
In combinatory logic, the application of a function to an argument, such as ![]() , is written
, is written ![]() or
or ![]() . Also, the need for functions of more than one variable is avoided by allowing the value of a function to be another function. For example, suppose, in traditional notation,
. Also, the need for functions of more than one variable is avoided by allowing the value of a function to be another function. For example, suppose, in traditional notation, ![]() . Then let
. Then let ![]() where
where ![]() . Then
. Then ![]() . In combinatory notation,
. In combinatory notation, ![]() and
and ![]() . In this notation, we use association to the left for application, so that
. In this notation, we use association to the left for application, so that ![]() .
.
This method of using only functions of one argument has come to be called currying, and the function ![]() of the previous paragraph is often called
of the previous paragraph is often called ![]() . Curry himself learned of this use of his name in his last years, and he protested because he had gotten the idea from Schönfinkel, but this use of Curry’s name has stuck.
. Curry himself learned of this use of his name in his last years, and he protested because he had gotten the idea from Schönfinkel, but this use of Curry’s name has stuck.
Other combinators are:
- The identity operator
 , with the property that
, with the property that 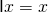 .
. - The constancy operator
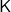 with the property that
with the property that 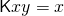 . Thus,
. Thus, 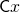 is a constant function whose value for any argument is
is a constant function whose value for any argument is 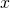 .
. - The compositor
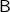 , with the property that
, with the property that 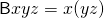 . This says that to apply
. This says that to apply 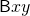 to
to  , first apply
, first apply 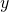 to
to  and then apply
and then apply 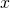 to the result.
to the result. - The diagonalizer
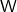 with the property that
with the property that 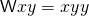 .
. - The distributor
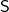 with the property that
with the property that 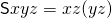 .
.
Note that ![]() can be defined in terms of the other operators, since
can be defined in terms of the other operators, since ![]() , so
, so ![]() . Also, since
. Also, since ![]() ,
, ![]() can be defined as
can be defined as ![]() .
.
Now suppose we want to say that an operation, say addition, is commutative (i.e. the order of adding does not matter). The traditional way of writing this in mathematics is ![]() . But this is not a property of
. But this is not a property of ![]() and
and ![]() ; it is a property of +. To say this in the language of combinatory logic, we would write
; it is a property of +. To say this in the language of combinatory logic, we would write ![]() . Now suppose we have an operator
. Now suppose we have an operator ![]() (for “commutator” with the property that
(for “commutator” with the property that ![]() . Then
. Then ![]() , and we can say that + is commutative by writing
, and we can say that + is commutative by writing ![]() . This operator
. This operator ![]() is called a combinator.
is called a combinator.
The defining rules for these combinators have been written above with the equality symbol, which is symmetric. But it is often useful to read these equations only from left to right. Then these equations would be called contractions, so that ![]() contracts to
contracts to ![]() ,
, ![]() contracts to
contracts to ![]() ,
, ![]() contracts to
contracts to ![]() ,
, ![]() contracts to
contracts to ![]() ,
, ![]() contracts to
contracts to ![]() , and
, and ![]() contracts to
contracts to ![]() . Terms are reduced to other terms by performing sequences of 0 or more contractions on subterms of the original term. For example, the reduction of
. Terms are reduced to other terms by performing sequences of 0 or more contractions on subterms of the original term. For example, the reduction of ![]() to
to ![]() is as follows:
is as follows:
![]() .
.
(Here I am using the symbol ‘![]() ‘ to indicate a reduction.) Note that there are some terms which cannot be reduced. These terms are said to be in normal form. On the other hand, some terms can lead to infinite reductions, for example
‘ to indicate a reduction.) Note that there are some terms which cannot be reduced. These terms are said to be in normal form. On the other hand, some terms can lead to infinite reductions, for example
![]() .
.
Curry decided to found mathematical logic on a system of combinators whose primitive combinators were ![]() and
and ![]() . (He did not yet understand the role of
. (He did not yet understand the role of ![]() , which he got from Schönfinkel.) The part of combinatory logic that deals with the basic properties of the combinatory terms without reference to logical connectives and quantifiers is now called pure combinatory logic. He was going to add logical connectives and quantifiers until he had developed a complete system of logic; this part of the subject he called illative combinatory logic. This word “illative” is a word Curry coined himself, based on the Latin word illatum, the past participle of infero, which means “to conclude”.
, which he got from Schönfinkel.) The part of combinatory logic that deals with the basic properties of the combinatory terms without reference to logical connectives and quantifiers is now called pure combinatory logic. He was going to add logical connectives and quantifiers until he had developed a complete system of logic; this part of the subject he called illative combinatory logic. This word “illative” is a word Curry coined himself, based on the Latin word illatum, the past participle of infero, which means “to conclude”.
He proved several important results in this context. First of all he proved that if ![]() is any combination of combinators and the variables
is any combination of combinators and the variables ![]() , there is a term
, there is a term ![]() in which the variables
in which the variables ![]() do not appear such that
do not appear such that ![]() . Curry used the notation
. Curry used the notation ![]() for this
for this ![]() . For example, since
. For example, since ![]() , we can take
, we can take ![]() to be
to be ![]() . He also gave axioms for the system so that this
. He also gave axioms for the system so that this ![]() was uniquely determined by
was uniquely determined by ![]() and the variables in question. (The existence of such an abstract for every term
and the variables in question. (The existence of such an abstract for every term ![]() and all variables
and all variables ![]() is called combinatory completeness.) Another of the things he proved early on (in his dissertation) is that the basic system of combinators, without any axioms for any logical connectives or quantifiers, is consistent.
is called combinatory completeness.) Another of the things he proved early on (in his dissertation) is that the basic system of combinators, without any axioms for any logical connectives or quantifiers, is consistent.
Using the notation of combinators, Curry wrote what is normally written ![]() as
as ![]() , where
, where ![]() . This operator
. This operator ![]() was present in his dissertation, but none of its properties were developed there. Instead, Curry started writing a series of papers expanding combinatory logic to include not only this universal quantifier
was present in his dissertation, but none of its properties were developed there. Instead, Curry started writing a series of papers expanding combinatory logic to include not only this universal quantifier ![]() , but also
, but also ![]() (for implication, so that
(for implication, so that ![]() , or if
, or if ![]() then
then ![]() ) and equality
) and equality ![]() , so that
, so that ![]() means
means ![]() . In 1934, Curry published [Curry 1934a] giving properties of
. In 1934, Curry published [Curry 1934a] giving properties of ![]() and
and ![]() .
.
b. The Kleene-Rosser Paradox and its Aftermath
In 1932, Curry learned of a paper by Alonzo Church, [Church 1932]. Church’s system was based on ![]() -abstraction, which forms terms from variables by application and abstraction: if
-abstraction, which forms terms from variables by application and abstraction: if ![]() is a variable and
is a variable and ![]() is a term, then
is a term, then ![]() is a term. (The outermost parentheses may be omitted if no confusion results.) For example,
is a term. (The outermost parentheses may be omitted if no confusion results.) For example, ![]() is the squaring function, and
is the squaring function, and ![]() . Here,
. Here, ![]() , which is an abbreviation for
, which is an abbreviation for ![]() , plays the role of Curry’s
, plays the role of Curry’s ![]() . (For a complete introduction to both
. (For a complete introduction to both ![]() -calculus and combinatory logic, see [Hindley and Seldin 2008]. See also the article on
-calculus and combinatory logic, see [Hindley and Seldin 2008]. See also the article on ![]() -calculi in this Encyclopedia.) Also, the variables
-calculi in this Encyclopedia.) Also, the variables ![]() in
in ![]() is called bound; variables not within the scope of a
is called bound; variables not within the scope of a ![]() are called free.
are called free.
Reduction for Church’s system is defined by a rule that Curry called ![]() :
: ![]() contracts to
contracts to ![]() , which is the result of substituting
, which is the result of substituting ![]() for
for ![]() in
in ![]() , where other bound variables are changed to avoid capture. In ordinary predicate logic, this sort of change is made by changing
, where other bound variables are changed to avoid capture. In ordinary predicate logic, this sort of change is made by changing ![]() to
to ![]() if a term in which
if a term in which ![]() occurs free is substituted for
occurs free is substituted for ![]() .
.
Note that reduction in Church’s system differs from reduction in combinatory logic in that if ![]() reduces to
reduces to ![]() , then
, then ![]() reduces to
reduces to ![]() , but in combinatory logic the fact that
, but in combinatory logic the fact that ![]() reduces to
reduces to ![]() does not automatically imply that
does not automatically imply that ![]() reduces to
reduces to ![]() , since subterms of
, since subterms of ![]() often do not really occur in
often do not really occur in ![]() .
.
In 1934, Curry received a letter from Rosser informing him that Kleene and Rosser had proved inconsistent the system of [Church 1932] and the system of [Curry 1934]. They did this by deriving Richard’s Paradox (See the article on Richard’s Paradox in this Encyclopedia.) in both systems.
Church and his students, Kleene and Rosser, then gave up on the idea of building a system of mathematical logic adequate for all of mathematics by basing the system on ![]() -terms. Instead, they took that part of Church’s system involving only
-terms. Instead, they took that part of Church’s system involving only ![]() -terms and treated it separately as the
-terms and treated it separately as the ![]() -calculus. (See the article on
-calculus. (See the article on ![]() -calculi But Curry had a different reaction. He had always considered the possibility that some systems he would propose might be inconsistent, and so he reacted by beginning a careful analysis of the paradox with the idea of finding a way to define a consistent system.
-calculi But Curry had a different reaction. He had always considered the possibility that some systems he would propose might be inconsistent, and so he reacted by beginning a careful analysis of the paradox with the idea of finding a way to define a consistent system.
This analysis lasted for several years, and by the time he took a leave of absence from Penn State to do applied mathematics for the U.S. government during World War II, he had developed a plan for research to look for consistent systems. He had already published [Curry 1941], and he had found a much simpler paradox (now known as Curry’s Paradox; see [Curry 1942b]). The plan he had developed was to look at three different kinds of systems, which differed in the logical connectives and quantifiers that were taken as primitive. The kinds of systems will be discussed here in the order Curry gave them in [Curry 1942a].
- Systems based on the theory of functionality. This was Curry’s idea, dating back to 1930, that led to type assignment. He wrote
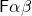 for the predicate of functions which take arguments in
for the predicate of functions which take arguments in 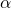 with values in
with values in 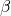 , and he intended
, and he intended 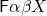 to mean
to mean 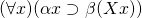 . Nowadays, the category (or predicate)
. Nowadays, the category (or predicate) 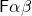 is considered a type rather than a predicate, and is usually written
is considered a type rather than a predicate, and is usually written 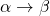 .
. - Systems based on the theory of restricted generality. Curry had noted that most universal quantification is not absolute, but is over some restricted domain. (This seems obvious nowadays, but in the 1930s it ran counter to the generalising tendency of Frege and Russell.) He defined an operator
 to stand for this restricted quantification, so that
to stand for this restricted quantification, so that  would stand for
would stand for 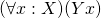 , or
, or 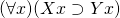 (where here
(where here 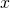 does not occur free in
does not occur free in 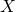 or
or 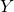 ).
). - Systems based on the theory of universal generality. These were systems based on
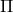 and
and 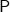 , where
, where 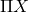 meant
meant 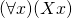 (where
(where 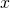 does not occur free in
does not occur free in 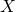 ) and
) and 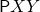 means
means 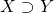 .
.
In 1942, Curry assumed that these kinds of systems increased in strength in the order given above. The paper [Curry 1942a] was really an abstract of future research rather than a report on completed work.
In the late spring of 1942, Curry finally came to understand the combinator ![]() . Rosser had published a paper on combinatory logic (based on different basic combinators from those Curry used), and he had shown how to define
. Rosser had published a paper on combinatory logic (based on different basic combinators from those Curry used), and he had shown how to define ![]() by induction on the structure of
by induction on the structure of ![]() . When Curry read this paper and translated the results into his own formalism, he realized why Schönfinkel had defined all combinators in terms of
. When Curry read this paper and translated the results into his own formalism, he realized why Schönfinkel had defined all combinators in terms of ![]() and
and ![]() , and he started to do the same. The use of
, and he started to do the same. The use of ![]() greatly increased the lengths of definitions of
greatly increased the lengths of definitions of ![]() compared with Curry’s original definition, but greatly simplified the algorithm for building them. With computer implementation has come a reversal of values: an algorithm’s speed of action is now valued more than its simplicity or “beauty”.
compared with Curry’s original definition, but greatly simplified the algorithm for building them. With computer implementation has come a reversal of values: an algorithm’s speed of action is now valued more than its simplicity or “beauty”.
c. Late Period (after World War II)
After World War II, when Curry returned to Penn State (For details, see the section of the Bibliography section of this article for Curry’s work during World War II.), he slowly got back into logic. He attended the Tenth International Congress of Philosophy in the summer of 1948, and as a result of a proposal made to him there, he decided to write a long work on combinatory logic, which he intended to include everything known on the subject. Feeling he needed a collaborator, he approached Robert Feys at Louvain in Belgium. Curry used a Fulbright which he was awarded for the year 1950-51 to start this work to start, and Curry and Feys continued to work on it after Curry returned to Penn State in 1951. Curry wound up working on this work and a second volume for most of the rest of his life.
The earliest work on this book was on the basic exposition. Curry and Feys completely revised the foundations of combinatory logic, and spent a lot of time explaining Curry’s approach to formal reasoning and formal systems. They then introduced Church’s ![]() -calculus, and gave a new proof and analysis of the Church-Rosser Theorem, which proves pure
-calculus, and gave a new proof and analysis of the Church-Rosser Theorem, which proves pure ![]() -calculus consistent. The book then took up combinatory logic itself, first pure combinatory logic and then illative combinatory logic. The book finishes with two chapters on the theory of fuctionality.
-calculus consistent. The book then took up combinatory logic itself, first pure combinatory logic and then illative combinatory logic. The book finishes with two chapters on the theory of fuctionality.
However, Curry soon began to start new research to be included. At first, this included work expanding the theory of functionality. There was always more than one such theory, and different theories depended on which terms could be what we would now call types, but which Curry called F-obs. There is the basic theory of functionality, in which types are formed from atomic types by the operation that forms ![]() from
from ![]() and
and ![]() . (This is equivalent to forming the type
. (This is equivalent to forming the type ![]() from
from ![]() and
and ![]() .) This system is easily proved consistent.
.) This system is easily proved consistent.
Then there is the full free theory of functionality, in which any combinatory term can be a type. Curry thought that this system was consistent, and in 1954 he tried to prove that consistency. He spent over four months at this attempt by trying to prove that if, from a set of typing assumptions ![]() (where
(where ![]() may be any combinatory terms), one can prove
may be any combinatory terms), one can prove ![]() then the deduction must take a certain specific form. After almost five months, he realized that if
then the deduction must take a certain specific form. After almost five months, he realized that if ![]() is the conclusion of any deduction in this special form, then the term
is the conclusion of any deduction in this special form, then the term ![]() is irreducible in some sense. But the sense involved was not the sense of reduction in combinatory logic, but rather the sense of
is irreducible in some sense. But the sense involved was not the sense of reduction in combinatory logic, but rather the sense of ![]() -calculus. The difference is that in
-calculus. The difference is that in ![]() -calculus, if
-calculus, if ![]() then
then ![]() , which is what one would expect. But in combinatory logic, the fact that
, which is what one would expect. But in combinatory logic, the fact that ![]() does not automatically imply that
does not automatically imply that ![]() , for subterms of
, for subterms of ![]() do not necessarily occur in
do not necessarily occur in ![]() .
.
For Curry, the fact that the term ![]() in the conclusion of a deduction in the theory of functionality must be irreducible in the sense of
in the conclusion of a deduction in the theory of functionality must be irreducible in the sense of ![]() -calculus was not very satisfactory. Curry usually thought in combinators rather than
-calculus was not very satisfactory. Curry usually thought in combinators rather than ![]() -terms. Thus, he set out to find a reduction among combinatory terms that would be more like
-terms. Thus, he set out to find a reduction among combinatory terms that would be more like ![]() -reduction. He began with
-reduction. He began with ![]() -reduction, which is
-reduction, which is ![]() -calculus in which the reduction rules include (
-calculus in which the reduction rules include (![]() ), the rule for changes of bound variables, (
), the rule for changes of bound variables, (![]() ), the basic reduction for
), the basic reduction for ![]() -calculus, which says that
-calculus, which says that ![]() , the result of substituting
, the result of substituting ![]() for
for ![]() in
in ![]() , and (
, and (![]() ), the rule which says that if
), the rule which says that if ![]() is not free in
is not free in ![]() , then
, then ![]() . He then defined strong reduction for combinatory logic that is equivalent to
. He then defined strong reduction for combinatory logic that is equivalent to ![]() -reduction. For technical reasons, he needed to take
-reduction. For technical reasons, he needed to take ![]() as a primitive combinator instead of defining it as
as a primitive combinator instead of defining it as ![]() as he had done previously, so now combinatory logic is usually defined by taking the three combinators
as he had done previously, so now combinatory logic is usually defined by taking the three combinators ![]() ,
, ![]() , and
, and ![]() as primitive combinators.
as primitive combinators.
Curry soon managed to prove that the full free theory of functionality is, in fact, inconsistent. The book [Curry and Feys 1958] ends with a chapter including the proof that the full free theory is inconsistent and also some results that are true that were proved as part of the failed attempt to prove it consistent.
This volume also includes the first published proof of the Normal Form Theorem, which says that every term with a type has a normal form. (A term is said to be in normal form if it cannot be reduced. It is said to have a normal form if it can be reduced to a term in normal form.) This result has become more and more important in various systems of typed ![]() -calculi in the decades since this volume was published.
-calculi in the decades since this volume was published.
In the years immediately after the publication of [Curry and Feys 1958], Curry began to work on systems of restricted generality. But he only published a couple of papers on this before he began work on [Curry et al. 1972]. This volume begins with addenda to pure combinatory logic, most of which are highly technical. Curry did try to devise a general framework that would include both combinatory logic and ![]() -calculus by defining what he called C-systems. The idea was to set up a framework that could be used to prove results in illative systems that were based either on
-calculus by defining what he called C-systems. The idea was to set up a framework that could be used to prove results in illative systems that were based either on ![]() -calculus or on combinatory logic without having to give separate proofs for the two cases. But this attempt was not completely successful, since it was later found that many results still needed one proof for
-calculus or on combinatory logic without having to give separate proofs for the two cases. But this attempt was not completely successful, since it was later found that many results still needed one proof for ![]() -calculus and another for combinatory logic.
-calculus and another for combinatory logic.
Curry also extended the definition of illative combinatory logic to include any systems with new atomic constants that have special postulates associated with them, even if these new constants do not represent logical connectives or quantifiers. This allowed him to include systems of combinatory arithmetic. Arithmetic had first been represented by Alonzo Church in combinatory logic and ![]() -calculus by defining natural numbers as iterators: the number
-calculus by defining natural numbers as iterators: the number ![]() is represented by
is represented by ![]() , which applies
, which applies ![]() to
to ![]()
![]() times. But by the 1960s, other ways of representing numbers as combinators or
times. But by the 1960s, other ways of representing numbers as combinators or ![]() -terms had appeared. For this reason, Curry suggested representing numbers by taking new atomic constants to represent 0 and the successor function (
-terms had appeared. For this reason, Curry suggested representing numbers by taking new atomic constants to represent 0 and the successor function (![]() ) and including a combinator that mapped one of these numbers to the corresponding iterator. With any of these representations, a function can be represented by a combinator or
) and including a combinator that mapped one of these numbers to the corresponding iterator. With any of these representations, a function can be represented by a combinator or ![]() -term if and only if it is partial recursive, or, equivalently, Turing-computable. (This result was first proved for
-term if and only if it is partial recursive, or, equivalently, Turing-computable. (This result was first proved for ![]() -calculus independently by Church, Kleene, and Turing in 1936; see, for example, [Kleene 1936c].)
-calculus independently by Church, Kleene, and Turing in 1936; see, for example, [Kleene 1936c].)
Curry also considered extensions of the results on the theory of functionality, including the introduction of a new typing operator ![]() with the rule that from
with the rule that from ![]() and
and ![]() follows
follows ![]() , so that the type of the value of a function may depend on the argument as well as on the type of the argument. The type
, so that the type of the value of a function may depend on the argument as well as on the type of the argument. The type ![]() is the type that is now usually denoted
is the type that is now usually denoted ![]() , and is usually called the dependent function type. However, the type was only introduced, and no systems based on it were developed by Curry.
, and is usually called the dependent function type. However, the type was only introduced, and no systems based on it were developed by Curry.
The rest of the book includes material on the theory of restricted generality and universal generality. It was shown that these kinds of systems are essentially equivalent. Systems were proved consistent that are essentially equivalent to first-order systems of logic by defining classes of canonical terms which are supposed to represent propositions and propositional functions. Attempts to find consistent systems in which the assumptions for terms to be canonical were stated as axioms of the logic were made, but most of the systems involved were later proved to be inconsistent. Finally, the theory of functionality was used to define systems of type theory in the traditional sense.
Curry spent the rest of his life continuing this work and other work he had done. The last problem he worked on was an attempt to find a reduction for combinatory terms that is equivalent to ![]() -reduction,
-reduction, ![]() -reduction in which the contraction rules are only (
-reduction in which the contraction rules are only (![]() ) and (
) and (![]() ). As of this writing, this problem is not yet settled. See Seldin’s papers [Seldin 2011] and [Seldin 2017].
). As of this writing, this problem is not yet settled. See Seldin’s papers [Seldin 2011] and [Seldin 2017].
3. Gentzen-style Proof Theory
Curry read Gentzen’s work [Gentzen 1934] two years after it appeared, and it did not take him long to realize that the ideas of that paper could be useful in finding a system of logic based on combinatory logic that could be proved consistent.
Gentzen had introduced two new formulations of logical systems: natural deduction systems and sequent calculi (L-systems). Natural deduction systems are covered in the article Deductive-Theoretic Conceptions of Logical Consequence in this encyclopedia. Sequent calculi are equivalent to natural deduction systems and are designed to search for proofs.
The consistency of natural deduction systems for propositional calculus and first-order predicate calculus follows from what is called the normalization theorem (due originally to Prawitz, [Prawitz 1965]). This result is equivalent to a result of Gentzen on sequent calculi: the cut elimination theorem. Curry worked out his own proof of the latter theorem. He also used a version of it to give the first published proof of the normal form theorem for ordinary basic functionality. (A proof by Turing from 1941 was not published until 1980; see [Gandy 1980b].)
Curry became convinced that a system of formal logic is not properly formalized unless there is a sequent calculus for it for which the cut elimination theorem can be proven.
Another feature of Curry’s approach is that he considered these systems as formalizing the elementary metatheory of what he called an elementary formal system. An elementary formal system is one in which there are no rules which discharge assumptions. Curry had such a formal system for combinatory logic. He used the idea that he was formalizing the elementary metatheory of an elementary formal system to justify all the operational rules. This illustrates that Curry was concerned with semantics.
4. War Work and Computing
When Curry first left Penn State to do applied mathematics for the U.S. Government, he began working on the mathematics of aiming a projectile at a moving target, the so-called fire control problem. Curry had studied this kind of mathematics as a student, and so he had little trouble doing this work during World War II.
By 1945, when Curry was at the Aberdeen Proving Ground, there was word that an electronic computer, the ENIAC, was being built for the purpose of calculating firing tables for the artillery. Curry was named to the committee that was being set up to evaluate the ENIAC when it was delivered. This committee first met in July, 1945, and early that month Curry attended a lecture on the ENIAC by Herman Goldstine. The next day, he decided to write a program to calculate the digits of ![]() , the base of the natural logarithms. He finished the program in early 1946, but whether it was ever run is uncertain. Curry later reported that nobody else that he knew at the time who was working on the ENIAC in 1946 could see the point of using a computer for a result assumed to be known.
, the base of the natural logarithms. He finished the program in early 1946, but whether it was ever run is uncertain. Curry later reported that nobody else that he knew at the time who was working on the ENIAC in 1946 could see the point of using a computer for a result assumed to be known.
In 1949, John von Neumann and some colleagues wrote and ran programs to calculate the digits of ![]() and
and ![]() . (See [Reitwiesner 1950a] and Reitwiesner et al. 1950b].) As a result, they discovered that the amateur mathematician William Shanks, who had spent over two decades starting in the middle of the 19th century calculating digits of
. (See [Reitwiesner 1950a] and Reitwiesner et al. 1950b].) As a result, they discovered that the amateur mathematician William Shanks, who had spent over two decades starting in the middle of the 19th century calculating digits of ![]() , and who had calculated to 707 digits, had made a mistake on digit number 528. The people who wrote the program in 1949 seem to have had no idea that Curry wrote such a program just a few years earlier. On the other hand, by 1949 there had been some changes in the ENIAC, and the program Curry wrote in 1945–46 might no longer have been compatible with the ENIAC.
, and who had calculated to 707 digits, had made a mistake on digit number 528. The people who wrote the program in 1949 seem to have had no idea that Curry wrote such a program just a few years earlier. On the other hand, by 1949 there had been some changes in the ENIAC, and the program Curry wrote in 1945–46 might no longer have been compatible with the ENIAC.
Curry also became involved in writing programs to do inverse interpolation on the ENIAC, programs useful for dealing with firing tables. See [de Mol et al. 2010].
Curry’s work on programming inverse interpolation on the ENIAC led him to develop a theory of programming. Curry’s basic approach was very similar to the approach he had taken two decades earlier in analyzing the process of substitution. He broke programs down into the simplest possible elementary components and then proposed using program composition to put them together again. This approach has been compared to the later development of compilers for user languages. See [Curry 1954].
However, Curry was not able to continue to work on this development because he could not persuade Penn State to buy any computer equipment in the late 1940s.
5. Formalism: the Philosophy of Mathematics
Curry developed a distinctive philosophy of mathematics. His views developed considerably over the course of his career, but he is mostly known for his earlier works on the subject.
Curry’s earliest philosophical work, dating from 1939, proposed to define mathematics as the science of formal systems. But Curry’s approach to formal systems was not quite the same as that of most others in the field.
The usual definition of a formal system begins by defining the formal objects as words on an alphabet of symbols, or, to use the terminology more current in computer science today, strings of characters. But then some of these words are picked out as “well formed formulas” by an inductive definition with the property that each well formed formula has a unique construction from the “atomic formulas”. For example, for the propositional calculus, we are given a possibly infinite set of atomic formulas ![]() , and a typical definition of well formed formula goes as follows:
, and a typical definition of well formed formula goes as follows:
- Every atomic formula is a well formed formula.
- If
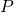 is a well formed formula, then
is a well formed formula, then 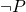 is a well formed formula.
is a well formed formula. - If
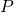 and
and 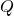 are well formed formulas, then
are well formed formulas, then 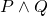 ,
, 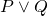 , and
, and 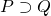 are well formed formulas.
are well formed formulas. - Nothing else is a well formed formula.
If the logical system involved includes quantifiers, then the atomic formulas are themselves defined, and that definition may depend on inductive definitions. For example, if we are defining a formal system for first-order logic, we start with terms, which are built up out of atomic terms and individual variables by using basic functions, and then we have predicates, from which the atomic formulas are obtained by applying them to terms. If the first order system is a system of arithmetic, we start with the atomic term 0 and functions denoted by ![]() (as a superscript) and
(as a superscript) and ![]() and
and ![]() (as infixes), and then terms are defined as follows:
(as infixes), and then terms are defined as follows:
- Every individual variable is a term.
- 0 is a term.
- If
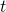 is a term, then so is
is a term, then so is 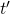 . (This is intended to denote the number that is one more than
. (This is intended to denote the number that is one more than 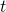 .)
.) - If
 and
and 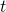 are terms, then
are terms, then 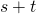 and
and 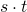 are terms. (The term
are terms. (The term 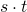 is often abbreviated as
is often abbreviated as 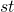 .)
.) - Nothing else is a term.
Once terms have been defined, atomic formulas are defined as follows:
- If
 and
and 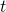 are terms, then
are terms, then 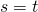 is an atomic formula.
is an atomic formula.
And then the following clause is added to the definition of well formed formula:
- If
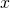 is an individual variable and
is an individual variable and 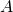 is a well formed formula, then
is a well formed formula, then 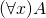 and
and 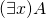 are well formed formulas.
are well formed formulas.
Curry noted is that although these definitions of term, atomic formula, and well formed formula say they are about strings of symbols on some alphabet, they do not really depend on that fact. For him, the crucial thing was that each term and well formed formula have a unique construction, whereas any word of three or more letters has more than one construction.(For example, the string ![]() can be formed in two ways:
can be formed in two ways: ![]() can be added to
can be added to ![]() on the right, or
on the right, or ![]() can be added to
can be added to ![]() on the left.) So while we obviously represent formal objects on a page or on a blackboard as strings of characters, it is not necessary that they actually be such strings. The strings may only be the names for these formal objects. It is only necessary that they are defined inductively so that each one has a unique construction.
on the left.) So while we obviously represent formal objects on a page or on a blackboard as strings of characters, it is not necessary that they actually be such strings. The strings may only be the names for these formal objects. It is only necessary that they are defined inductively so that each one has a unique construction.
Also, formal systems do not need to be systems of logic in the ordinary sense with logical connectives and quantifiers. It is possible to have a simpler formal system. An example Curry gave is what he called the “system of Sams” for natural numbers. (He got this name from the Hungarian word for number, which is szám.) In this system, the formal objects are interpreted as natural numbers. There is one primitive formal object, which I will name “0”. There is one operation, which forms ![]() from
from ![]() . The rules for forming the sams are as follows:
. The rules for forming the sams are as follows:
- 0 is a sam.
- If
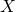 is a sam, then so is
is a sam, then so is 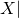 .
. - Nothing else is a sam.
There is one predicate, which forms ![]() from sams
from sams ![]() and
and ![]() . Thus, the elementary statements are those of the form
. Thus, the elementary statements are those of the form ![]() , where
, where ![]() and
and ![]() are sams. There is one axiom, namely
are sams. There is one axiom, namely
0 = 0
There is also one rule of inference: From ![]() to deduce
to deduce ![]() . This is a very simple formal system, and it is easy to show that the theorems (provable elementary statements) are those of the form
. This is a very simple formal system, and it is easy to show that the theorems (provable elementary statements) are those of the form ![]() , where
, where ![]() is a sam.
is a sam.
In saying that mathematics is the science of formal systems, Curry was claiming that (pure) mathematics does not really have a subject matter. It was not what he called a contensive topic. (The word contensive is a word Curry coined to express the idea of the German word inhaltlich.) Of course, mathematical statements do have subjects and therefore subject matter, but Curry claimed that the only subject matter any mathematical statements had was other mathematics.
Curry’s attitude towards truth was that truth comes in two kinds:
- Truth within a formal system (or within a given theory). This depends on how the system or theory is defined.
- The acceptability of a system (or theory) for some purpose. This depends on the purpose, and Curry took this pragmatically.
In his work on combinatory logic and Gentzen proof theory, he preferred to use only constructive logic in the metatheory, this would be accepted by more people than classical logic. (In this, he did not see that most mathematicians were not familiar with constructive mathematics.) On the other hand, he had no trouble accepting classical logic in the mathematics to be used in physics. In a sense, Curry did not really believe in one absolute notion of truth.
On the other hand, once formal systems (or any other kind of theories) are created, they have properties which can be investigated, and hence have objective existence. In this sense, Curry believed in the idea that Karl Popper introduced later of the third world. In fact, Popper presented this idea at a session of the Third International Congress of Logic, Methodology, and Philosophy of Science in Amsterdam in 1967, and as it happened Curry was the chair of the session. (See [Popper 1968].) After Popper’s presentation was over, Curry told his graduate student Jonathan P. Seldin, who was also present, that he thought that Popper had made a big deal out of something that was trivially and obviously true.
Over his career, Curry changed several times the words he used to denote the formal objects of a formal system. In his earliest work on combinatory logic, he called them “entities” (using the German word Etwas as a noun in his dissertation, which was written in German). However, in a discussion with a philosopher (whom he did not name in his later years), he was told that his use of that word implied some philosophical conclusions with which he disagreed. At that point, he decided to use the word “term” instead. It is now common to refer to “combinatory terms” and “![]() -terms”. However, this caused him a problem when he was dealing with a formal system of logic with quantifiers, since the terms would be what are usually called “formulas”, and there are other formal objects called “terms”. So in the end, he coined his own word by taking the first syllable of the word “object”, and started calling them obs. To some people, the word ob appeared to refer specifically to combinatory logic, but in fact Curry used the word for formal objects of any kind of formal system.
-terms”. However, this caused him a problem when he was dealing with a formal system of logic with quantifiers, since the terms would be what are usually called “formulas”, and there are other formal objects called “terms”. So in the end, he coined his own word by taking the first syllable of the word “object”, and started calling them obs. To some people, the word ob appeared to refer specifically to combinatory logic, but in fact Curry used the word for formal objects of any kind of formal system.
In his later work, Curry extended his definition of formal system to allow for systems whose formal objects are strings of characters. He called such systems syntactical systems, and called his earlier kind of formal systems ob systems.
Also in his later work, Curry also extended his definition of mathematics from saying that mathematics is the science of formal systems to saying that mathematics is the science of formal methods. This definition should be sufficiently broad to include all of mathematics, since if we compare piles of apples and oranges by seeing if there is a one-to-one correspondence between them, we are looking at the forms of the piles rather than the content (apples or oranges).
Curry chose the name “formalism” for his philosophy of mathematics because of David Hilbert. However, Curry’s idea of formalism is very different from the idea of other philosophers of mathematics who call themselves formalists. It is probably better to think of Curry’s formalism as a kind of structuralism.
6. References and Further Reading
a. Primary Sources
- [Curry 1929] Curry, Haskell B., An analysis of logical substitution”, American Journal of Mathematics 51, 363-384.
- Curry’s first published paper, written as part of an application for a grant to go to Gottingen.
- [Curry 1930] Curry, Haskell B., Grundlagen der kombinatorischen Logik”, American Journal of Mathematics 52 (1930) 509-536, 789-834.
- Curry’s dissertation, written in German at Gottingen in 1928-1929. Republished with a translation into English and an introduction on Curry’s work by Fairouz Kamareddine and Jonathan P. Seldin as Foundations of Combinatory Logic by College Publications, 2016.
- [Curry 1934a] Curry, Haskell B., Some properties of equality and implication in combinatory logic”, Annals of Mathematics (2) 34, 381-404.
- This is the paper that gave Kleene and Rosser what they needed to prove inconsistent the systems of Church and Curry.
- [Curry 1934b] Curry, Haskell B., Functionality in combinatory logic”, Proceedings of the National Academy of Sciences U.S.A., 20, 584-590.
- An extended abstract of item 1936 below, which Curry had some trouble getting accepted for publication because the approach originally looked strange.
- [Curry 1936] Curry, Haskell B., First properties of functionality in combinatory logic,” Tohoku Mathematical Journal 41 Part II, 371-401.
- Curry’s first paper on functionality. He originally wrote it in 1932, but had trouble getting it accepted for publication. The version published in 1936 contains many misprints.
- [Curry 1939] Curry, Haskell B., Remarks on the definition and nature of mathematics”, Journal of Unified Science 9, 164-169, and reprinted many times since.
- Curry’s first work on the philosophy of mathematics.
- [Curry 1941] Curry, Haskell B., The paradox of Kleene and Rosser”, Transactions of the American Mathematical Society, 50, 454-516.
- Curry’s study of the paradox mentioned in the title.
- [Curry 1942a] Curry, Haskell B., Some advances in the combinatory theory of quantication”, Proceedings of the National Academy of Sciences U.S.A. 28, 564-569.
- This is the paper Curry wrote just before his leave of absence from Penn State to do war work in which he set out his plans to try to send consistent systems of logic based on combinatory logic.
- [Curry 1942b] Curry, Haskell B., The inconsistency of certain formal logics”, Journal of Symbolic Logic 7, 115-117.
- [Curry 1949] Curry, Haskell B., A simplication of the theory of combinators”, Synthese 7, 391-399.
- The paper in which Curry published his understanding of the combinator S.
- [Curry 1950] Curry, Haskell B., A Theory of Formal Deducibility, (Indiana University Press).
- Curry’s first book on Gentzen-style proof theory.
- [Curry 1951] Curry, Haskell B., Outlines of a Formalist Philosophy of Mathematics (Amsterdam, North-Holland).
- This was mostly written in 1939 and is essentially the long manuscript from which the paper of 1939 was prepared as a shorter version.
- [Curry 1954] Curry, Haskell B., The logic of program composition”, In Applications Scientiques de la Logique Mathematique, Actes du 2e Colloque International de Logique Mathematiques, Paris 25-30 Aout 1952, Institut Henri Poincare, (Paris: Gauthier-Villars and Louvain: Nauwelaerts). Curry’s summary of his theory of programming.
- [Curry and Feys 1958] Curry, Haskell B. and Feys, Robert, Combinatory Logic, Volume I, (Amsterdam, North-Holland).
- The first volume of Curry’s great work on combinatory logic.
- [Curry 1963] Curry, Haskell B., Foundations of Mathematical Logic, (McGraw-Hill, and since reprinted by Dover).
- Curry’s major work on Gentzen-style proof theory.
- [Curry et al. 1972] Curry, Haskell B., Hindley, J. Roger, and Seldin, Jonathan P., Combinatory Logic, Volume II, (Amsterdam, North-Holland).
- The second volume of Curry’s great work on combinatory logic.
b. Secondary Sources (by year)
- [Russell and Whitehead 1910-1913] Russell, Bertrand and Whitehead, Alfred North, Principia Mathematica, 3 volumes (Cambridge University Press).
- The first major work on logic that Curry read.
- [Schönfinkel 1924] Schönfinkel, Moses, Über die Bausteine der mathematischen Logik”, Mathematische Annalen 92, 305-306.
- A work that Curry first encountered in 1927-28 which, much to his surprise, had anticipated his own idea for combinators. The paper was written by Behman, and was a report on a seminar talk Schonnkel had given at Gottingen in 1920. An English translation has appeared as “On the building blocks of mathematical logic”, in From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931, edited by Jean van Heijenoort (Harvard University Press, 1967), pp. 355-366.
- [Hilbert 1925] David Hilbert, Über das Unendliche”, Mathematische Annalen 95 (1925) 161-190.
- One of the most important papers Hilbert wrote on the foundations of mathematics. Reprinted (in German) in David Hilbert, Hilbertiana: Fünf Aufsätze (Darmstadt: Wissenschaftliche Buchgesellschaft, 1964), pp. 79-108. Translation into English published as “On the infinite” in Jean van Heijenoort (editor), From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931, (Cambridge, MA and London, England: Harvard University Press 1967), pages 367-392.
- [Heyting 1930] Heyting, Arend, Die formalen Regeln der intuitionistischen Logik”‘, Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-Mathematische Klasse 1930, 42-56.
- The paper in which Heyting introduced his formal system of intuitionistic logic.
- [Church 1932] Church, Alonzo, A set of postulates for the foundation of logic”, Annals of Mathematics (2) 33, 346-366.
- The paper in which Church first introduced abstraction as part of a larger system.
- [Gentzen 1934] Gentzen, G., Untersuchungen über das logische Schliessen”, Mathematische Zeitschrift 39, 405-431.
- The paper in which Gentzen introduced his systems of natural deduction and his L-systems (sequent calculi).
- [Kleene 1935] Kleene, Steven C. and Rosser, J. Barkley, The inconsistency of certain formal logics”, Annals of Mathematics (2) 36, 630-636.
- The paper in which Kleene and Rosser published their proof of the contradiction in the systems of Church and Curry.
- [Church and Rosser 1936a] Church, Alonzo and Rosser, J. Barkley, Some properties of conversion”, Transactions of the American Mathematical Society 39, 472-482.
- The paper in which the Church-Rosser Theorem was first proved for lambda-calculus.
- [Church 1936b] Church, Alonzo, An undecidable problem in elementary number theory’, American Journal of Mathematics 58, 345-363.
- The paper in which Church proved that there is a problem in elementary number theory which cannot be decided by an algorithm. The paper includes a statement by Church that a function is partial recursive if and only if it can be represented by a -term, a result that he and Kleene obtained independently about the same time.
- [Kleene 1936c] Kleene, Steven C., “-denability and recursiveness”, Duke Mathematical Journal 2, 340-353.
- The paper in which Kleene first proved that a function is partial recursive if and only if it can be represented by a -term, a result he discovered independently at the same time Alonzo Church did. This formed part of the justication of the Church-Turing thesis, that a function is mechanically computable if and only if it is partial recursive if and only if it is Turing computable if and only if it is -denable.
- [Rosser 1942] Rosser, J. Barkley, New sets of postulates for combinatory logics”, Journal of Symbolic Logic 7, 18-27.
- Rosser’s paper that enabled Curry to understand the combinator S, although Rosser did not use that combinator.
- [Reitwiesner 1950a] Reitwiesner, George W., An ENIAC determination of pi and e to more than 2000 decimal places”, Mathematical Tables and Other Aids to Computation, 4, 11-15.
- A paper on the program run on the ENIAC to calculate digits of and e in 1949-1950. The paper shows no indication of any knowledge of the program Curry wrote to do this for e in 1945-46.
- [Reitwiesner et al. 1950b] Metropolis, N. C., Reitwiesner, G., and von Neumann, J., Statistical treatment of the values of first 2,000 decimal digits of e and calculated on the ENIAC”, Mathematical Tables and Other Aids to Computation, 4, 109-111.
- The statistical analysis of the results of the program run on the ENIAC as described by George W. Reitwiesner.
- [Prawitz 1965] Prawitz, Dag, Natural Deduction: A Proof-Theoretical Study, Almqvist & Wiksell, 1965. Reprinted by Dover in 2006.
- This was originally Prawitz’ doctoral dissertation, and introduced Prawitz’ ideas of proof reduction and proof normalization.
- [Popper 1968] Popper, K. R., Epistemology without a knowing subject”, in van Rootselaar, B. and Staal, J. F. (editors), Logic, Methodology and Philosophy of Science III: Proceedings of the Third International Congress for Logic, Methodology and Philosophy of Science, Amsterdam 1967, (Amsterdam: North-Holland), pp. 333{373.
- This is the paper in which Popper introduced his idea of the third world. The paper had been presented in the first session of the congress (11:15 a.m. to 12:00 noon, with H. B. Curry in the chair) under the title “Epistemology and scientic knowledge”. See the program of the congress on p. 543 of the proceedings.
- [Hindley and Seldin 1980a] Hindley, J. Roger and Seldin, Jonathan P. (editors), To. H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism, (Academic Press).
- A collection of papers related to Curry’s work. Includes a short biography and a complete list of Curry’s publications.
- [Gandy 1980b] Gandy, R. O., An early proof of normalization by A. M. Turing”, in [1980a], pp. 453{455.
- This is Turing’s earliest proof of the normal form theorem for typed-calculus with an introduction by Gandy.
- [Hindley and Seldin 2008] Hindley, J. Roger and Seldin, Jonathan P., Lambda-Calculus and Combinators, An Introduction, (Cambridge University Press).
- A general introduction to lambda-calculus and combinatory logic.
- [de Mol et al. 2010] de Mol, Liesbeth, Bullynck, Maarten, and Martin, Carle, “Haskell before Haskell. Curry’s contribution to programming (1946-1950)”, in Ferreira, F., Lowe, B, Mayordomo, E., and Gomes, L.M. (Eds.), Programs, Proofs, Processes, 6th Conference on Computability in Europe, CIE, 2010, Ponta Delgada, Azores, Portugal, June 30-July 4, 2010, Springer Lecture Notes in Computer Science, vol. 6158, pp. 108-117.
- A paper on Curry’s theory of programming.
- [Seldin 2011] Seldin, Jonathan P., “The search for a reduction in combinatory logic equivalent to -reduction”, Theoretical Computer Science 412, 4905-4918.
- A paper describing the attempt to find a reduction in combinatory logic equivalent to -reduction, including a discussion of the technical problems involved.
- [Seldin 2017] Seldin, Jonathan P., The search for a reduction in combinatory logic equivalent to -reduction, Part II, Theoretical Computer Science 663, 34-58.
- A paper giving the proofs of the key properties of the proposals given in Seldin 2011.
Author Information
Jonathan P. Seldin
Email: jonathan.seldin@uleth.ca
University of Lethbridge
Canada
