The Sheffer Stroke
The Sheffer Stroke is one of the sixteen definable binary connectives of standard propositional logic. The stroke symbol is “|” as in
![]()
The linguistic expression whose logical behavior is presumed modeled by this logical connective is the truth-functional phrase “not both,” from which the name NAND originates.
All sixteen connectives interpret associated functions of the Boolean algebra. In the theory of electronic circuits the Boolean functions are implemented by electronic or logic gates: the gate implementing the associated function of the Sheffer Stroke is called NAND and is known as a “universal gate.” The Sheffer Stroke has the remarkable metalogical property known as functional completeness (more precisely, weak functional completeness.) A connective is functionally complete (more precisely, weakly functionally complete) for a formal language ![]() if and only if all mathematically definable connectives of
if and only if all mathematically definable connectives of ![]() (except for the zeroary connectives or constants) can be defined by using that connective as the only connective. In using the familiar truth table for the semantics of the standard propositional logic, the functional completeness of the Sheffer Stroke means that, for every truth table labeled by a well-formed formula of the logic, there is an identical truth table whose labeling formula has the Sheffer Stroke symbol as the only connective symbol; or, every definable connective can be defined by a truth table that is labeled by a formula that has the Sheffer Stroke as its only connective symbol. (Two truth tables are identical if they agree on every truth value output corresponding to the same truth value input assignments.) The same observations about functional completeness apply to the case of the Peirce Arrow, which is the dual of the Sheffer Stroke.
(except for the zeroary connectives or constants) can be defined by using that connective as the only connective. In using the familiar truth table for the semantics of the standard propositional logic, the functional completeness of the Sheffer Stroke means that, for every truth table labeled by a well-formed formula of the logic, there is an identical truth table whose labeling formula has the Sheffer Stroke symbol as the only connective symbol; or, every definable connective can be defined by a truth table that is labeled by a formula that has the Sheffer Stroke as its only connective symbol. (Two truth tables are identical if they agree on every truth value output corresponding to the same truth value input assignments.) The same observations about functional completeness apply to the case of the Peirce Arrow, which is the dual of the Sheffer Stroke.
The discovery of the Sheffer Stroke was achieved independently by Henry M. Sheffer in 1913 after it had been realized previously by Charles Sanders Peirce, as attested by a fragment written in 1880 (and, again, in 1902). This landmark discovery was hailed by such seminal figures in the history of logic as Ludwig Wittgenstein and Bertrand Russell.
An elegant result due to Emile Post (1941) makes it possible to account for the property of functional completeness of the Sheffer Stroke on the grounds that it is lacking certain characteristic “hereditary” properties. This is examined in detail in the present article.
The logical-philosophic significance of the availability of a Sheffer function was taken by Ludwig Wittgenstein (in the Tractatus Logico-Philosophicus, 1922) to consist in its perspicuous illustration of deeper features of formal logic. In natural languages, the phrases whose logical behavior is captured by the Sheffer Stroke and the Peirce Arrow are, respectively, “not both” and “neither-nor”: these seem rather unremarkable, but this is a sign that what is at stake in functional completeness investigations is characteristically related to the study of formal logic and is not relevant to the goals of studying natural languages.
Table of Contents
- The Sheffer Stroke and Its Place in Propositional Logic
- History
- The Logical Connectives of Standard Propositional Logic and the Sheffer Stroke
- Properties of the Sheffer Stroke
- Significance of the Sheffer Stroke for Mathematical Logic, Philosophical Logic,
and Philosophy - References and Further Reading
1. The Sheffer Stroke and Its Place in Propositional Logic
The linguistic phrase whose logical behavior is traced through the Sheffer Stroke is the truth-functional expression “not both ___ and —,” and its logical equivalent is “either not ___ or not —.” The term “Sheffer Stroke” is the name of the symbol “ ![]() ” denoting the binary logical connective of the standard Propositional Logic that is usually called Sheffer Stroke. Thus, the name Sheffer Stroke is used not simply for the symbol but also for the logical connective itself. This article refers to the logical connective indifferently as the Sheffer Stroke trusting that context removes any ambiguity between the connective and its symbol.
” denoting the binary logical connective of the standard Propositional Logic that is usually called Sheffer Stroke. Thus, the name Sheffer Stroke is used not simply for the symbol but also for the logical connective itself. This article refers to the logical connective indifferently as the Sheffer Stroke trusting that context removes any ambiguity between the connective and its symbol.
Other names of the logical connective are Alternate Denial, NAND and Negated Conjunction. Readers of older Logic textbooks are likely to find the connective called Alternate Denial. There is another, related, logical connective of standard propositional logic, called NOR, Joint Denial, Negated Disjunction, and Joint Exclusion; it is sometimes called Peirce’s Arrow or Quine’s Dagger (although the last two, as with “Sheffer Stroke” are, strictly speaking, names of symbols used for that connective.) The relationship between the Sheffer Stroke and NOR is deep and has profound interest, which will be explored in this article.
Other names of the logical connective are Alternate Denial, NAND and Negated Conjunction. Readers of older Logic textbooks are likely to find the connective called Alternate Denial. There is another, related, logical connective of standard propositional logic, called NOR, Joint Denial, Negated Disjunction, and Joint Exclusion; it is sometimes called Peirce’s Arrow or Quine’s Dagger (although the last two, as with “Sheffer Stroke” are, strictly speaking, names of symbols used for that connective.) The relationship between the Sheffer Stroke and NOR is deep and has profound interest, which will be explored in this article.
The term “Sheffer Stroke” refers also to the symbol used to denote the logical connective that has the same name; this connective is also known by other names, as will be seen. This article speaks of logical connectives. Strictly speaking, the Sheffer Stroke connective is the semantic analogue of a definable binary Boolean function which can be called the associated Boolean function of the connective. This Boolean function is known as NAND in the theory of electronic or logic gates, where it serves as one of two universal gates; precisely speaking, the physical gate is an instance of implementation of the Boolean function whose propositional-logic interpretation is the Sheffer Stroke. That interpretation is not examined in the present article.
This article focuses only upon propositional logic, unless otherwise indicated. Upon turning to the examination of Wittgenstein’s comments, this restriction will be lifted. Propositional logic can be considered as the special case of predicate or first-order logic with all predicate constants as being zero-place in its signature. Propositional logic is bereft of symbolic resources needed for checking many argument forms as valid, for the translation of mathematical statements, and for many other reasons. This article is confined to propositional logic only for the limited purpose of avoiding certain complications while our present interest is in laying out certain basic concepts.
The term Sheffer Functions is sometimes used to refer to two Boolean functions, one of which is interpreted as our Sheffer Stroke and the other is known as NOR (in some interpretations) or Peirce’s Arrow (and also by other names, as will be seen.) Both of these so-called Sheffer functions are binary truth functions (with the names also used for the uninterpreted associated Boolean functions); they both have the remarkable property of being functionally complete—in the sense defined above. The term “Sheffer functions” is also used to refer to functionally complete functions of alternate or non-standard many-valued logics. Some authors who generalize the term “Sheffer function” to many-valued logics define it so that it applied only to unary or binary functions that are, each, functionally complete. Others use the term regardless of the arity of the functionally complete function. A theorem proven by Emile Post in 1921 shows that proven existence of functions of arity n = 1 or n = 2 that define all unary and binary functions of a formal language implies that those functions can also define all functions of higher arities. This result holds regardless of the number of truth values over which the connectives are defined. In the standard two-valued propositional logic, there are no unary connectives that are functionally complete but there are exactly two binary connectives that are, and these are called the Sheffer functions of the standard propositional logic.
The kind of inquiry that reveals the remarkable properties of the Sheffer Stroke is, properly speaking, metalogical or metatheoretical. The two logical connectives, NAND (or the Sheffer Stroke) and NOR, are sometimes referred to summarily as the Sheffer functions. Strictly speaking, those are the associated Boolean functions which are semantically interpreted by the logical connectives. For present purposes, this article does not dwell on this distinction. It speaks consistently about logical connectives. The article investigates the significance of the Sheffer Stroke and NOR in the section on the Properties of the Sheffer Stroke. It also traces the historical background of the discovery of these connective. (see History)
Note that there is inconsistency in the bibliography with respect to both notational variants and terminological jargon. The logician H. M. Sheffer, after whom the connective is named, actually used NOR but Russell-Whitehead used the NAND function when they extolled this discovery in a specially added section to the second edition of their famed Principia Mathematica in the aftermath of what they took to be Sheffer’s discovery. (Whitehead-Russell, 1925, 1927) It was Whitehead-Russell who gave the name “Sheffer Stroke” to the connective. Although the symbol itself had been used by Sheffer to denote NOR, Sheffer rather incongruously called the symbol of his connective “per”, in analogy with the symbol of algebraic division, and he called the connective (now usually called NOR) “rejection.”
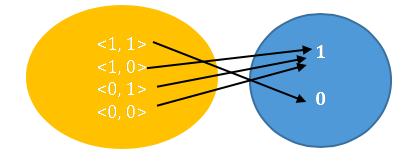
As a logical connective, the Sheffer Stroke stands for a Boolean function defined over the set of two values,
![]()
Insofar as the semantic connective Sheffer Stroke is being examined, think of the values as the truth values True and False and denote them respectively by T and F. It is not unusual to speak interchangeably, or indifferently, of truth functions and logical connectives. Unfortunately, as it was just noted, the bibliography, ranging over several decades in the development of modern logic, is not consistent when it comes to terminological or notational matters. For present purposes, lay down a certain convention: distinguish between logical connectives (also called truth functions) and their underlying or associated Boolean functions. If the symbol of the logical connective is, generally, “![]() ” then symbolize the associated Boolean function by “
” then symbolize the associated Boolean function by “![]() .” In doing so, reserve standard algebraic methods of definition for the associated functions but define the logical connectives by means of the familiar truth table.
.” In doing so, reserve standard algebraic methods of definition for the associated functions but define the logical connectives by means of the familiar truth table.
The domain ![]() of the associated function of the Sheffer Stroke
of the associated function of the Sheffer Stroke ![]() is the Cartesian product
is the Cartesian product
![]()
the range ![]() of the function is
of the function is
![]()
Thus, the associated function of the Sheffer Stroke connective is defined as follows:
![]()
For the sake of completeness, alternative ways of defining this Boolean function will be shown. These, however, should be considered as notational variants; it is the same Boolean function that they all define.
![]()
when
![]()
otherwise
![]()
It is customary to define logical connectives of logical systems or languages by means of the familiar truth table. The truth table for the connective called the Sheffer Stroke or NAND is given below.
| p | q | p |
|
q |
| T | T | T | F | T |
| T | F | T | T | F |
| F | T | F | T | T |
| F | F | F | T | F |
One can also use the familiar truth table to ascertain that the Sheffer Stroke connective receives the same truth value outputs with the negation of conjunction for all possible assignments of truth values to the individual propositional components. The propositional connective negation, by definition, reverses the truth values of its inputs and the conjunction connective receives the output T only when both of its inputs are T while it receives F for all other possible assignments of truth values to its components. This article symbolizes the negation connective by “![]() ” and the conjunction connective by “
” and the conjunction connective by “![]() ”. Because the formulas written in bold are logically equivalent, the formula formed by connecting them with “
”. Because the formulas written in bold are logically equivalent, the formula formed by connecting them with “![]() ” (symbol of material equivalence) should be a tautology: the truth table verifies this result. (The logical connective of material equivalence is so defined that it receives the output T if and only if its input values are the same truth values.)
” (symbol of material equivalence) should be a tautology: the truth table verifies this result. (The logical connective of material equivalence is so defined that it receives the output T if and only if its input values are the same truth values.)
| p | q | (p |
|
q) |
|
|
(p |
|
q) |
| T | T | T | F | T | T | F | T | T | T |
| T | F | T | T | F | T | T | T | F | F |
| F | T | F | T | T | T | T | F | F | T |
| F | F | F | T | F | T | T | F | F | F |
The linguistic expression whose logical behavior is presumed modeled by this logical connective is the truth-functional phrase “not both,” from which the name NAND originates. This expression is logically equivalent (it yields the same truth value for the same assignments of truth values to its components) with “either not the first or not the second” for two component propositions; hence the alternative name of this connective as Alternate Denial. Making the claim that the Sheffer Stroke connective models such expressions of language means that what is modeled is taken to be truth-functional expressions of a natural language like English. Truth-functionality means that the compound proposition always takes a truth value (true or false) that can be uniquely determined when the truth values of the components or parts are known; this is because the special logical particle (in this case “not both”) that connects the component propositions is definable in terms of its truth conditions (what truth value it yields for specified assignments of truth values to the component propositions it connects). Insofar as one is dealing with truth-functional expressions, the Principle of Compositionality of Meaning applies: the logical meaning of the composite depends uniquely on the specified logical meanings of its parts. For non-truth-functional meanings of “not” or “and,” the expression “not both” is not truth-functional and cannot be modeled by the connective called Sheffer Stroke or NAND.
Connecting two propositions by means of the linguistic particle modeled by the Sheffer Stroke asserts the claim that these two propositions are mutual contraries. One can appreciate what contrariety means by checking the truth table above, by means of which the Sheffer Stroke connective is defined: the compound in which the Sheffer Stroke symbol is the principal-connective symbol is false only when the connected propositional components are both true; it is true in every other case (or model, which means assignment of truth values to the propositional components or, also called, valuation.) Contrariety (or mutual contrariety), then, means that the propositions that are presumed contraries cannot possibly be true together but they can possibly be false together. One should distinguish this from the relationship known as mutual contradictoriness: two propositions are mutual contradictories if and only if they cannot possibly be true together and they cannot possibly be false together. If two propositions p and q are mutual contradictories, then the compound proposition formed by connecting them by means of the exclusive either-or is a logical truth. On the other hand, based on what has been said, and as can be seen by the truth table above, one has: when two propositions are mutual contraries, then the proposition formed by connecting them by means of the Sheffer Stroke connective is a logical truth.
a. Alternative Definitions of the Sheffer Stroke
There are other ways of defining the Sheffer Stroke connective. Its matrix definition is as follows:
|
|
T | F |
| T | F | T |
| F | T | T |
The Disjunctive Normal Form (DNF) of
![]()
is
![]()
(Corner brackets are used because there is reference to symbols of the formal object language within the metalanguage, which is a symbolically enhanced fragment of English used to talk about the formal language. Notice that symbols like “![]() ”, on the other hand, are themselves metalinguistic and do not take corner brackets. No such brackets are needed also in the case in which the formulas are presented by themselves in space reserved for them.)
”, on the other hand, are themselves metalinguistic and do not take corner brackets. No such brackets are needed also in the case in which the formulas are presented by themselves in space reserved for them.)
The DNF of a well-formed formula ![]() can be obtained from the truth table of
can be obtained from the truth table of ![]() by means of the following method: Check the rows, and only the rows, across which
by means of the following method: Check the rows, and only the rows, across which ![]() receives the truth value T. If an individual (or atomic) variable receives T on that row, reproduce it as it is,
receives the truth value T. If an individual (or atomic) variable receives T on that row, reproduce it as it is, ![]() ; if the individual variable receives F on that row, reproduce it as negated.
; if the individual variable receives F on that row, reproduce it as negated. ![]() . Next, form the conjunction of the propositional variables so represented (which means that one connects them by the connective symbol
. Next, form the conjunction of the propositional variables so represented (which means that one connects them by the connective symbol ![]() .) Do this for all rows on which
.) Do this for all rows on which ![]() receives T. Finally, join all the conjunctions formed in this manner by means of inclusive disjunctions, symbolized by
receives T. Finally, join all the conjunctions formed in this manner by means of inclusive disjunctions, symbolized by ![]() .
.
Thus, examining the truth table by means of which the Sheffer Stroke was defined, one has: the value T is received on the rows for values of the single propositional variables:
![]()
Form the conjunctions first:
![]()
Then, form their conjunction:
![]()
This expression admits of further simplification (a subject that is beyond current concerns), to yield a logically equivalent formula:
![]()
A method of representation known as the Karnaugh Map is as follows for the Sheffer Stroke. Two different variants of this method are explored. This is essentially diagrammatic as it allows for simplifications of well-formed formulas that are first transformed into their equivalent normal forms before they are mapped by this type of diagram. The normal form for the Shefer Stroke is:
![]()
The expression to the right is in both Disjunctive and Conjunctive Normal Form. It has exactly two literals, ![]() and
and ![]() . Taken as a Disjunctive Normal Form, it has as literals the negations of the two propositional variables: accordingly, we enter into the Karnaugh Map the values T and F in a way we will present now briefly. (Usually, this kind of diagram takes the values as uninterpreted or numerical,
. Taken as a Disjunctive Normal Form, it has as literals the negations of the two propositional variables: accordingly, we enter into the Karnaugh Map the values T and F in a way we will present now briefly. (Usually, this kind of diagram takes the values as uninterpreted or numerical,
![]()
but we can disregard this.) To enter the proper values, we follow the entire row or entire column along which the variable receives the truth value True as shown below. The remaining blocks receive F.
|
|
|
|
|
|
F | T |
|
|
T | T |
An alternative version (actually corresponding more closely to the initial design of this diagrammatic method) is as follows:
|
|
|
|
|
|
F | T |
|
|
T | T |
In older texts, we find definitions of connectives like the following definition of the Sheffer Stroke. We consider the propositional variables to be taking truth values in the order:
![]()
This method of definition is found, along with the truth-tabular definition, in Wittgenstein’s Tractatus.
In textbooks like the one written by Arthur Prior (1962, pp. 5-21) the definition would be given as follows:
Because Prior uses the Polish notation (see section 1c below), he defines the Sheffer Stroke and Peirce Arrow, symbolized respectively by “D” and “X”, as follows—with “N” symbolizing negation, “A” symbolizing inclusive disjunction, “K” symbolizing conjunction, while prefix notation is used throughout:
![]()
![]()
Another way of defining the Sheffer Stroke and Peirce Arrow is given (Prior, 1962, p. 12), reading the output values from left to right inside the parenthesis as corresponding to value assignments for the atomic components as
![]()
![]()
![]()
In the set-theoretic interpretation of Boolean functions, the operation that corresponds to the Sheffer Stroke or NAND is complementation of intersection of sets. Clearly, complementation (symbolized by “![]() ” is the set-theoretic analogue of negation and intersection (symbolized by “
” is the set-theoretic analogue of negation and intersection (symbolized by “![]() ”) is the set-theoretic analogue of conjunction. The symbol “
”) is the set-theoretic analogue of conjunction. The symbol “![]() ” stands for set membership.
” stands for set membership.
![]() it is not the case that both
it is not the case that both ![]() and
and ![]()
A Venn diagram can be drawn of the operation.
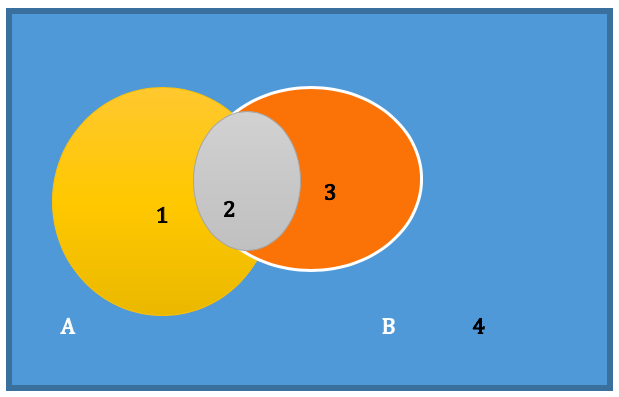
NAND Venn Diagram (yellow area)
Boolean functions can be represented as operations in an algebra,
![]()
with carrier set ![]() and adequately equipped with a set of operations of multiplication and addition-modulo-2 along with the constant or zero-ary function 1. The definitions of the operations over the carrier set’s values are:
and adequately equipped with a set of operations of multiplication and addition-modulo-2 along with the constant or zero-ary function 1. The definitions of the operations over the carrier set’s values are:
![]()
![]()
The Sheffer Stroke and Peirce Arrow are definable in this algebra as:
![]()
![]()
The multiplication sign is omitted as is conventional in standard notations. So, we have:
![]()
![]()
Considering that the general form for binary polynomials representing functions is
![]()
the coefficients are
![]()
The general form can also be represented as follows and, by having recourse to the familiar semantic truth table, we can determine the values of the coefficients which are, in this representation form, the values of the function for the shown pairs (i.e., ![]() ).
).
![]()
By carrying out the operations in the algebra, we obtain the expected result, keeping in mind that (2 = 0) (modulo 2):
![]()
b. Decision-Procedural Rules for the Sheffer Stroke
The decision procedure in propositional logic known as the Tree Method, can incorporate rules for “![]() ” as follows:
” as follows:


In the Beth-Tableau Method, the rules for “![]() ” should be represented as follows:
” should be represented as follows:


It is possible to develop a Gentzen-sequent rule for the Sheffer Stroke. (See Riser, 1967; Béziau, 2001; for a more detailed analysis, Read, 1999.) The theoretical significance of enacting proof-theoretic procedures, like Gentzen’s, consists in that the connectives are then defined by means of the rules for their introductions and/or eliminations; there is a substantive philosophic view that this is the proper approach to assessing the meanings of logical connectives. In Gentzen-style sequents, the variables to the left of the turnstile symbol (“![]() ”) are presumed joined by conjunction and those to the right are presumed joined by inclusive disjunction. A variable may be shifted from left to right or from right to left by being negated. Repeated variable letters may be deleted (by means of a rule known as Contraction) and variable letters may be shifted freely (or permuted) insofar as they stay in the same side of the turnstile.
”) are presumed joined by conjunction and those to the right are presumed joined by inclusive disjunction. A variable may be shifted from left to right or from right to left by being negated. Repeated variable letters may be deleted (by means of a rule known as Contraction) and variable letters may be shifted freely (or permuted) insofar as they stay in the same side of the turnstile.
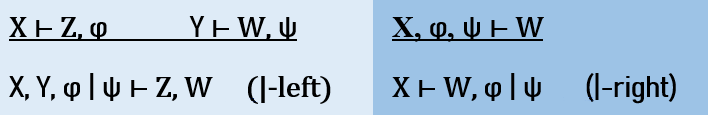
c. Alternative Symbols
Another symbol for the Sheffer Stroke or NAND connective is “![]() ” and this symbol is, appropriately, called the “Sheffer Dagger” or “Sheffer Upward Arrow.” An older symbol is “
” and this symbol is, appropriately, called the “Sheffer Dagger” or “Sheffer Upward Arrow.” An older symbol is “![]() ” (for instance, in Alonzo Church’s influential text on Mathematical Logic, Introduction to Mathematical Logic, p. 37), but this symbol is now more commonly used in certain notational variants to symbolize exclusive disjunction. (See History below for symbols used by Sheffer himself and by C. S. Peirce.)
” (for instance, in Alonzo Church’s influential text on Mathematical Logic, Introduction to Mathematical Logic, p. 37), but this symbol is now more commonly used in certain notational variants to symbolize exclusive disjunction. (See History below for symbols used by Sheffer himself and by C. S. Peirce.)
In Polish notation, which uses not infix but prefix placement for connective symbols and neatly dispenses with parentheses, the symbolization for NAND is:
![]()
To write in Polish notation that material equivalence (symbolized by “![]() ”) obtains between NAND and the negation (symbolized by “
”) obtains between NAND and the negation (symbolized by “![]() ”) of conjunction (symbolized by “
”) of conjunction (symbolized by “![]() ”), we write:
”), we write:
![]()
The symbolic variant used for logical gates in electronic circuitry also deploys prefix notation (with the symbol of the function written before and not in between the input variables. Thus,
![]()
As the case usually is with writing out functions, it should be noted that there is ambiguity surrounding the notation used for representing the Boolean function interpreting the Sheffer Stroke: it is not clear if it is the operation that is represented or if a name of the function is given. The notation of the so-called lambda-calculus (or ![]() -calculus) can be used to disambiguate. Accordingly, to indicate unambiguously that we are giving the name of the underlying function of the NAND (or Sheffer Stroke) connective, we can write:
-calculus) can be used to disambiguate. Accordingly, to indicate unambiguously that we are giving the name of the underlying function of the NAND (or Sheffer Stroke) connective, we can write:
with possible specification of the underlined input variables from the set ![]()
2. History
The logical connective we call the Sheffer Stroke and its symbol are named after Henry Maurice Sheffer who, in 1913, published a paper in which he introduced a connective (called a “primitive idea” in the jargon of the times) with remarkable logical properties. Sheffer’s project was motivated by the purpose of using this connective to provide a more parsimonious or economical rendering of Huntington’s axiom system for standard propositional logic. In the parlance of the times, the purpose was to “reduce” the number of “primitive” connectives of standard propositional logic. We will see in subsequent section what all this amounts to.
It so happens that Sheffer used another logical connective which, like the Sheffer Stroke, allows for a reduction of the number of logical connectives that are used. This connective is usually called NOR, Peirce’s Arrow or Joint Denial. The name Sheffer’s Stroke was coined by the authors of Principia Mathematica (Whitehead-Russell, 1963) who extolled the significance of the discovery of this connective and proceeded to add an entire section to the 2![]() edition of the Principia utilizing the connective. We will be able to fully appreciate the claims made about the significance of this discovery after we have studied the section on the Properties of the Sheffer Stroke. An entire section, Significance of the Sheffer Stroke for Mathematical Logic, Philosophical Logic, and Philosophy, will be devoted to assessing the importance of this connective.
edition of the Principia utilizing the connective. We will be able to fully appreciate the claims made about the significance of this discovery after we have studied the section on the Properties of the Sheffer Stroke. An entire section, Significance of the Sheffer Stroke for Mathematical Logic, Philosophical Logic, and Philosophy, will be devoted to assessing the importance of this connective.
Sheffer himself had called his connective “rejection,” inspired by the correspondence of this connective to the linguistic expression “neither-nor.” Another name that was once in usage for this connective is “dispersion.” As we have mentioned, this connective is usually called NOR or Peirce’s Arrow today. Sheffer called the propositional variables that are the connective’s related variables or inputs “rejects.” Rather inopportunely, he gave to the connective symbol the name “per” in analogy to the name of the symbol of the standard algebraic division: in terms of the underlying algebra of modern propositional logic, however, there is no satisfactory Boolean analogue to algebraic division and, so, the name “per” is misleading.
a. Peirce’s Discovery
It turns out that the American logician and philosopher Charles Sanders Peirce (1839-1914) had already discovered the logical connective we call the Sheffer Stroke, as well as the related connective NOR (also called Joint Denial, and quite appropriately Peirce’s Arrow, with other names in use being Quine’s Arrow or Quine’s Dagger and today usually symbolized by “![]() ”). The relevant manuscript, dating to 1880, numbered MS 378 in a subsequent edition and titled “A Boolian [sic] Algebra with One Constant” (Peirce, 1971), was actually destined for discarding and was salvaged for posterity literally at the nick of time in 1926. A fragmentary text by Peirce dating from 1880 also shows familiarity with the remarkable metalogical characteristics that make a single function functionally complete, and this is also the case with Peirce’s unfinished Minute Logic (1902, ch. 3): these texts were eventually published posthumously (1933, vol. 4, pp. 13-18, 215-216.)
”). The relevant manuscript, dating to 1880, numbered MS 378 in a subsequent edition and titled “A Boolian [sic] Algebra with One Constant” (Peirce, 1971), was actually destined for discarding and was salvaged for posterity literally at the nick of time in 1926. A fragmentary text by Peirce dating from 1880 also shows familiarity with the remarkable metalogical characteristics that make a single function functionally complete, and this is also the case with Peirce’s unfinished Minute Logic (1902, ch. 3): these texts were eventually published posthumously (1933, vol. 4, pp. 13-18, 215-216.)
Peirce designated the two truth functions, NAND and NOR, by using the symbol “![]() ” which he called Ampheck, coining this neologism from the Greek word ἀμφήκης which means “of equal length in both directions.” (Peirce, 1933: 4.264) Peirce’s editors disambiguated the use of symbols by assigning “
” which he called Ampheck, coining this neologism from the Greek word ἀμφήκης which means “of equal length in both directions.” (Peirce, 1933: 4.264) Peirce’s editors disambiguated the use of symbols by assigning “![]() ” to the connective we call the Sheffer Stroke while preserving the symbol “
” to the connective we call the Sheffer Stroke while preserving the symbol “![]() ” for NOR.
” for NOR.
(More about Peirce’s work in logic, including reference to the 1880 manuscript, can be found in another encyclopedia article.)
Like Sheffer did later, Peirce understood that these two connectives can be used to “reduce” all mathematically definable connectives (also called “primitives” and “constants”) of propositional logic: this means that all definable connectives of propositional logic can be defined by using only the Sheffer Stroke or NOR as the single connective. No other connective (or associated function) that takes one or two variables as inputs has this property. Standard, two-valued propositional logic has no unary functions that have the property of functional completeness. In subsequent section, we will explore this remarkable logical property in detail. At first blush, availability of this option ensures that economy of resources can be obtained—at least in terms of how many functions or connectives are to be included as undefined. Unfortunately, there is a trade-off between this gain in economy of symbolic resources and the unwieldy length and rather counterintuitive appearance of the formulas that use only the one connective.
It is characteristic of Peirce’s logical genius and emblematic of his rather under-appreciated contributions to the development of modern logic that he grasped the significance of functional completeness and figured out what truth functions—up to arity 2—are functionally complete for two-valued propositional logic. (Strictly speaking, this is the property of weak functional completeness, given that we disregard whether constants or zero-ary functions like 1 or 0 can be defined.) Peirce subscribed to a Semeiotic view, according to which the fundamental nature and proper tasks of the formal study of logic are defined by the rules set down for the construction and manipulation of symbolic resources. A proliferation of symbols for the various connectives that are admitted into the signature of a logical system suffers from a serious defect on this view: the symbolic grammar fails to match or represent the logical fact of interdefinability of the connectives. Peirce was willing sometimes to accept constructing a formal signature for two-valued propositional logic by using the two-members set of connectives ![]() , which is minimally functionally complete. This means that these two connectives—or, if we are to stick to an approach that emphasizes the notational character of logical analysis, these two symbols—are adequate expressively: every mathematically definable connective of the logic can be defined by using only these two; and the set is minimally functionally complete in the sense that neither of these connectives can be defined by the other (so, as we say, they are both independent relative to each other.) The symbol
, which is minimally functionally complete. This means that these two connectives—or, if we are to stick to an approach that emphasizes the notational character of logical analysis, these two symbols—are adequate expressively: every mathematically definable connective of the logic can be defined by using only these two; and the set is minimally functionally complete in the sense that neither of these connectives can be defined by the other (so, as we say, they are both independent relative to each other.) The symbol ![]() can be viewed as representing a constant truth function (either unary or binary) that returns the truth value False for any input or inputs. Or it can be regarded as a constant, which means that it is a zeroary (zero-input) function, a degenerate function, which refers to the truth value False. Although not using our contemporary terminology, Peirce took the second option. This set has cardinality 2 (it has exactly two members) but it is not the best we can do. Peirce’s discovery of what we have called the Sheffer Functions (anachronistically and unfairly to Peirce, but bowing to convention) shows that we can have a set of cardinality 1 (a one-member set or a so-called singleton) that is minimally functionally complete with respect to the definable connectives of two-valued propositional logic. Thus, either one of the following sets can do. The sets are functionally complete and, because they have only one member each, we say that the connectives themselves have the property of functional completeness.
can be viewed as representing a constant truth function (either unary or binary) that returns the truth value False for any input or inputs. Or it can be regarded as a constant, which means that it is a zeroary (zero-input) function, a degenerate function, which refers to the truth value False. Although not using our contemporary terminology, Peirce took the second option. This set has cardinality 2 (it has exactly two members) but it is not the best we can do. Peirce’s discovery of what we have called the Sheffer Functions (anachronistically and unfairly to Peirce, but bowing to convention) shows that we can have a set of cardinality 1 (a one-member set or a so-called singleton) that is minimally functionally complete with respect to the definable connectives of two-valued propositional logic. Thus, either one of the following sets can do. The sets are functionally complete and, because they have only one member each, we say that the connectives themselves have the property of functional completeness. ![]() is the symbol of the Sheffer Stroke or NAND and
is the symbol of the Sheffer Stroke or NAND and ![]() is the symbol of the Peirce Arrow or NOR. (We stipulate as such, even though we have not introduced our grammar formally.)
is the symbol of the Peirce Arrow or NOR. (We stipulate as such, even though we have not introduced our grammar formally.)
It is important to show, albeit briefly, how these functions can define other functions. Algebraically approached, this is a matter of functional composition but we do not enter into such details here. We will have more details in subsequent sections. In case one wonders why the satisfaction with defining the connectives of the set that comprises the symbols for negation, inclusive disjunction, and conjunction, namely ![]() , there is an explanation: there is an easy, although informal, way to show that this set is functionally complete. It is not minimally functionally complete because
, there is an explanation: there is an easy, although informal, way to show that this set is functionally complete. It is not minimally functionally complete because ![]() and
and ![]() are inter-definable. But it is functionally complete. Thus, showing that one can define these functions suffices for achieving functional completeness. Definability should be thought as logical equivalence: one connective can be defined by means of others if and only if the formulas in the definition (what is defined and what is doing the defining) are logically equivalent. (Presuppose the truth-tabular definitions of the connectives.)
are inter-definable. But it is functionally complete. Thus, showing that one can define these functions suffices for achieving functional completeness. Definability should be thought as logical equivalence: one connective can be defined by means of others if and only if the formulas in the definition (what is defined and what is doing the defining) are logically equivalent. (Presuppose the truth-tabular definitions of the connectives.)
![]()
![]()
![]()
![]()
![]()
![]()
b. The “Discovery” and Principia Mathematica
Bertrand Russell hailed this development (which he considered to be Sheffer’s “discovery”) and, with the co-author of Principia Mathematica Alfred Whitehead, added an entire section in the 2![]() edition to take advantage of the discovery. Russell was not aware that Peirce had already made the discovery in the 19
edition to take advantage of the discovery. Russell was not aware that Peirce had already made the discovery in the 19![]() century. Prompted by this applause and urged on by the weight of renewed expectations, Sheffer, who was not a prolific author, returned to the task of taking further advantage of his discovery, but he did not succeed in advancing beyond his initial contribution.
century. Prompted by this applause and urged on by the weight of renewed expectations, Sheffer, who was not a prolific author, returned to the task of taking further advantage of his discovery, but he did not succeed in advancing beyond his initial contribution.
Not only did Russell hail this discovery, but also the oracular thinker and profoundly influential philosopher Ludwig Wittgenstein (Tractatus, 1922) used grandiloquent language in celebrating the discovery that the “ideal” formal language of standard logic can be “reduced” to a single “primitive.” What this all means is discussed in the section on the Significance of the Sheffer Stroke for Mathematical Logic, Philosophical Logic, and Philosophy. Two other influential authors of an early logic textbook, David Hilbert and Wilhelm Ackermann, regarded this development as a rather unimpressive detail.
Despite the hullabaloo about the “single primitive,” efforts to take advantage of this result for constructing economical versions of Predicate Logic were sparse. No doubt, one reason is that a system that would have only the Sheffer Stroke as its connective would require use of unwieldy formulaic expressions. Abbreviation conventions would be needed, at a minimum. Another reason for the neglect, at least in Quine’s case, was that he was similarly preoccupied with generating other, similarly parsimonious, notational variants of logic (including variable-free grammars.) It was Moses Schönfinkel, one of the originators of Combinatory Logic, who adopted the Sheffer Stroke as single connective to construct a notational idiom of predicate logic. (See Bimbó, 2010.)
3. The Logical Connectives of Standard Propositional Logic and the Sheffer Stroke
It is time to briefly introduce a notational variant or idiom of standard propositional logic (SPL), within which one can locate the truth function NAND (or Sheffer’s Stroke); by referring to this formal language, one can examine and explicate the properties and significance of the Sheffer Stroke. Because one wants to be able to refer to other logical connectives besides the Sheffer Stroke, one actually lays out an expanded variant of SPL, which is called here SPLexp. Talk about SPLexp is within a fragment of English; this fragment is enhanced with specially designated symbols and, as such, it serves as our Metalanguage (ML) while SPLexp is the Object Language (OL). The next goal is to obtain ML symbols from the OL, and this is done without danger of ambiguity because the context makes clear whether OL or ML is employed. As is customary, when symbols are mentioned rather than used, they are placed within quotation marks.
The formal language SPLexp has symbolic resources for single or atomic propositional variables (up to the infinity of the natural numbers), and for logical connectives. It also has auxiliary symbols, and parentheses to be used only for the sake of preventing ambiguity of well-formed expressions. The metalinguistic symbol “![]() ” means “___ is a member of set —”. For connectives, the expansive idiom includes symbols for all definable unary and binary connectives of the standard propositional logic. For present purposes, there is no need to supply names for all the definable connectives denoted by these symbols. Definitions of the connectives are given by means of the familiar truth table. In brief,
” means “___ is a member of set —”. For connectives, the expansive idiom includes symbols for all definable unary and binary connectives of the standard propositional logic. For present purposes, there is no need to supply names for all the definable connectives denoted by these symbols. Definitions of the connectives are given by means of the familiar truth table. In brief,
Standard grammatical conventions for the construction of well-formed formulas are used.
N is the set of natural numbers. “![]() ” denotes the truth value of a well-formed formula
” denotes the truth value of a well-formed formula ![]() . Symbols from the object language are appropriated, trusting that the context removes ambiguity.
. Symbols from the object language are appropriated, trusting that the context removes ambiguity.
There are 2![]() = 4 unary connectives, and there are 2
= 4 unary connectives, and there are 2![]() raised to the second power = 16 binary connectives that are mathematically definable in the standard (two-valued) propositional logic. (In general, if n is the number of inputs to the connective, the number of mathematically definable n-ary connectives in standard propositional logic is 2
raised to the second power = 16 binary connectives that are mathematically definable in the standard (two-valued) propositional logic. (In general, if n is the number of inputs to the connective, the number of mathematically definable n-ary connectives in standard propositional logic is 2![]() raised to the n
raised to the n![]() power.)
power.)



Some characteristic equivalences, which can be checked by the familiar truth table method, are:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. Properties of the Sheffer Stroke
An examination of the properties of the Sheffer Stroke begins after having the formal idiom SPLexp in place. Introductory logic textbooks usually omit references to the special properties of the Sheffer Stroke; more advanced logic texts and mathematical logic or metalogic texts always make special mention of this connective and of its dual, the NOR or Peirce Arrow connective. (What “duality” means in this context will be examined soon.)
The student of logic learns that the Sheffer Stroke or NAND, like NOR, has a remarkable characteristic that is called functional completeness or expressive completeness. No other unary or binary connective, besides the Sheffer Stroke and its dual NOR, has this property. No connective of lesser arity (thus, zeroary or unary) has this property, either. When alternative logics are investigated, a fundamental metalogical task consists in querying the existence of functionally complete functions, which may be called Sheffer Functions. Present observations are limited to what is known as standard (sometimes called classical) logic: when it comes to alternative or non-classical logics, the connective defined as negation of conjunction should not be presumed to have the property of functional completeness. (It should be borne in mind that negation and conjunction themselves have different, non-standard, meanings in alternative logics since they are defined over more than the two truth values of standard logic.)
After defining functional completeness, it will be shown that indeed the Sheffer Stroke (or NAND) possesses this remarkable property. One needs to ask also why this is the case and why this is an important characteristic.
This property, functional or expressive completeness, is not to be confused with what is called simply “completeness.” Completeness in that sense means this: relative to what are the logical truths of a formal language ![]() , whose logical consequence relation is symbolized as “
, whose logical consequence relation is symbolized as “![]() ”, a proof system L is complete if and only if L’s derivability relation, symbolized “
”, a proof system L is complete if and only if L’s derivability relation, symbolized “![]() ”, is such that:
”, is such that:
This is equivalent to:
Roughly, what this means is that a complete system, and only a complete system, will have failures of proof or failures of derivation in all the cases, and only in the cases, in which one expects the corresponding semantical language to be failing in establishing semantic conclusions or logical truths. Think of a logical truth as a semantical conclusion of any, including the empty, set of premises.
There is more about this fundamental topic of Metalogic in other articles (see Propositional Logic and references there), but caution is needed here to note that functional completeness is not related to that other concept called simply “completeness.”
A logical connective
of a formal language
is functionally complete with respect to
if and only if every mathematically definable logical connective
of
can be defined in terms only of
.
For the case of a binary connective ![]() that is functionally complete, all mathematically definable connectives
that is functionally complete, all mathematically definable connectives ![]() can be defined by using only propositional variables and the connective
can be defined by using only propositional variables and the connective ![]() .
.
If one wants to define functional completeness in terms of the familiar semantic device of the truth table, one can do so in the following way:
a connective
is functionally complete for the language of standard propositional logic if and only if the truth tables for all mathematically definable connectives (of any arity) can be constructed with labels on the top arrow having the symbol for
as the only connective symbol.
For example, this can be done by using only the Sheffer Stroke symbol, ![]() , for certain familiar connectives of the standard propositional logic. Two truth tables are considered identical if they agree on all the truth value outputs corresponding to the same valuations (truth value assignments as inputs.) Thus, the truth-tabular definition of
, for certain familiar connectives of the standard propositional logic. Two truth tables are considered identical if they agree on all the truth value outputs corresponding to the same valuations (truth value assignments as inputs.) Thus, the truth-tabular definition of ![]() coincides with the truth table with outputs as in “
coincides with the truth table with outputs as in “![]() /
/![]() ” and the truth-tabular definition of
” and the truth-tabular definition of ![]() coincides with the truth table whose output column is as in “
coincides with the truth table whose output column is as in “![]() /
/![]() ”. Notice that the labels for
”. Notice that the labels for ![]() /
/![]() and
and ![]() /
/![]() use propositional variables and the only connective symbol they use is of
use propositional variables and the only connective symbol they use is of ![]() .
.
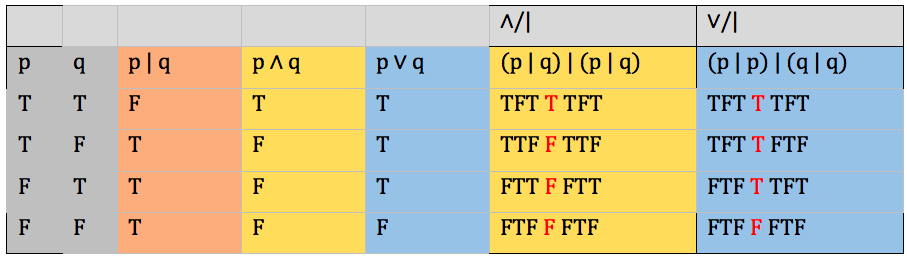
An alternative and equivalent definition is:
a connective
is functionally complete for the language of standard propositional logic if and only if for every truth table labeled by a well-formed formula of the logic there is an identical truth table whose label has the Sheffer Stroke symbol as the only connective symbol.
(Two truth tables are identical if they agree on every truth value output corresponding to the same truth value input assignments.)
The non-trivial question now faced is whether such functionally complete connectives are definable and how high one has to ascend in arity (to unary, binary, and so on) before finding a functionally complete connective. The answer is that one can stop at the level of binary connectives in the case of the standard two-valued logic: the Sheffer functions (the Sheffer Stroke and NOR) are, each, functionally complete. The details are examined below.
One can also define functional completeness as a property of groups or sets of connectives. Sometimes one finds references to functional completeness as a property of systems of connectives.
A set
of connectives is functionally complete with respect to a formal language
if and only if every mathematically definable connective
of
can be defined by using only members of
.
Such a set ![]() is then itself a member of the set of functionally complete sets of the language,
is then itself a member of the set of functionally complete sets of the language, ![]() . Thus, using “
. Thus, using “![]() ” as the symbol for set membership,
” as the symbol for set membership,
![]()
This means that the one-member set (singleton set) with the Sheffer Stroke as its only member is a functionally complete set or is a member of the set of functionally complete sets.
Of special interest is a proper subset of the functionally complete sets of connectives ![]() : sets that are minimally or non-redundantly functionally complete,
: sets that are minimally or non-redundantly functionally complete, ![]() . Here is what this means.
. Here is what this means.
A set
of logical connectives is minimally functionally complete (MFC) if and only if it is functionally complete (FC) and also it is the case that no connective in the set can be defined by using other connectives in the set.
If so, then each connective in the set is independent of the other connectives or simply independent.
Now, consider the set that is comprised only of the Sheffer Stroke connective:
![]()
This set is functionally complete. Since it has only one member, this set has to be MFC (minimally functionally complete) if it is FC (functionally complete). This is because there is only one connective; so, it is impossible for it to be defined in terms of other connectives in the set: this connective has to be independent! There are exactly two such MFC singletons in standard propositional logic (up to binary connectives):
![]()
![]()
This section concludes by highlighting certain other properties possessed by the Sheffer Stroke connective. This is done because having those properties is the underlying reason that the Sheffer Stroke connective is functionally complete. This brief investigation of those properties and of how they are related to functional completeness encapsulates the results established by the mathematicians Emil Post (1921, 1941) and William Wernick (1942).
1. Before examining the relationship between functional completeness and certain other logical properties of the Sheffer Stroke, there is a straightforward way of establishing that
![]()
is FC (functionally complete). To do this, consider how one can use the truth-tabular definition of any connective to extract its Disjunctive Normal Form (DNF). Here is an example. The same can be done with any connective regardless of its arity. This example is of a ternary or three-place connective. Extra columns are added to the truth table for illustrative purposes. In these columns the truth values of the individual propositional variables are traced across the rows in which the connective receives T as its truth value; then, it is shown how the DNF is formed.

Consider the Disjunctive Normal Form (DNF) of the given ternary connective. The method is this: form conjunctions of the atomic propositional variables across each row in which the connective receives the truth value T; the variables are written as seen in the added row of the example. Then form the inclusive disjunction of the conjunctions constructed in the previous step. Based on this truth table and the DNF that can be obtained, the definition of this connective in DNF could be given as follows:
![]()
A note about formal grammar: One takes advantage of the associativity of conjunction, inclusive disjunction and equivalence to omit unnecessary parentheses without ambiguity: when a connective ![]() is associative, “(
is associative, “(![]() ” and “
” and “![]() ” are equivalent; hence, they can both be written as “
” are equivalent; hence, they can both be written as “![]() ”. Note omission of outer parentheses.
”. Note omission of outer parentheses.
Because the above can be done for any connective, one can conclude that the set
![]()
is FC (functionally complete): any mathematically definable connective of the propositional language can be defined by using only connectives from the set ![]() . This includes the unary connectives. First, notice that negation is included in the set
. This includes the unary connectives. First, notice that negation is included in the set ![]() . The other three unary connectives are also definable as shown below.
. The other three unary connectives are also definable as shown below.
![]()
And when it comes to connectives of arity ![]() , the truth table shows the way to define them by using only connectives from the set
, the truth table shows the way to define them by using only connectives from the set ![]() , as above.
, as above.
The set
![]()
is functionally complete, as just established, but it is not minimally functionally complete. There is redundancy in it because the connectives conjunction and inclusive disjunction are inter-definable as can be seen in light of the following so-called DeMorgan equivalences:
![]()
![]()
The following two sets are not only FC (functionally complete) but also MFC (minimally functionally complete):
![]()
![]()
Now consider the Sheffer Stroke. In order to show that the set ![]() is FC, show that negation and either conjunction or inclusive disjunction are definable in terms of the Sheffer Stroke. Because
is FC, show that negation and either conjunction or inclusive disjunction are definable in terms of the Sheffer Stroke. Because ![]() and
and ![]() are, each, functionally complete, if the symbolized connectives in any one of these sets are definable in terms of the connective in
are, each, functionally complete, if the symbolized connectives in any one of these sets are definable in terms of the connective in ![]() , then this latter set also must be functionally complete.
, then this latter set also must be functionally complete.
It can be shown that, indeed, negation and inclusive disjunction, as well as conjunction, are definable in terms of the Sheffer Stroke. The truth table method can be used to verify that the following equivalences indeed obtain:
![]()
![]()
![]()
These equivalences can be justified in another way. Taking advantage of certain valid equivalences of the standard propositional logic, which are used to make replacements of phrases by their equivalents without alteration to truth value, one has:
![]()
![]()
![]()
2. Emil Post (1921, 1941; see also Pelletier and Martin, 1990) showed that any set ![]() of definable logical connectives of the standard propositional logic is functionally complete if and only if
of definable logical connectives of the standard propositional logic is functionally complete if and only if ![]() is not a subset of any of the following sets of connectives:
is not a subset of any of the following sets of connectives:
- the set of monotonic connectives (MC(
 ));
)); - the set of linear (also called countable, counting, or affine) connectives (L(
 ));
)); - the set of self-dual connectives (SD(
 ));
)); - the set of truth-preserving connectives (TP(
 ));
)); - and the set of falsehood- (or falsity-) preserving connectives (FP(
 )).
)).
If one single logical connective ![]() is to be functionally complete by itself (or if the singleton set with the function symbolized by
is to be functionally complete by itself (or if the singleton set with the function symbolized by ![]() as its only member is functionally complete), then the function
as its only member is functionally complete), then the function ![]() must lack all of the above properties of connectives. In other words,
must lack all of the above properties of connectives. In other words,
 should not be monotonic;
should not be monotonic; should not be linear;
should not be linear; should not be self-dual;
should not be self-dual; should not be truth-preserving;
should not be truth-preserving; should not be falsehood-preserving.
should not be falsehood-preserving.
After briefly defining these interesting properties, it can be shown that, among definable binary connectives, only the Sheffer functions (the Sheffer Stroke or NAND and the Peirce Arrow or NOR) lack all of those properties when one considers all the definable unary and binary connectives of the standard propositional logic. If one is examining a set of functions to determine whether it is functionally complete, check that there is at least one function in the set, which lacks one of the above properties; and perform this check for each property. So, one needs to ensure that, for each of the properties above, there is at least one function that lacks this property.
One can engage briefly the deeper analysis behind this seminal result, which can be called the Post Result (while the test presented above can be called the Post Test): All the enumerated properties are so-called Hereditary Properties. This means that if a function ![]() (or corresponding semantic connective) has a property like this, then all functions that can be defined by using only
(or corresponding semantic connective) has a property like this, then all functions that can be defined by using only ![]() must also have this property. This means that every such hereditary property
must also have this property. This means that every such hereditary property ![]() is “inherited” necessarily by all functions that are defined by means only of the function
is “inherited” necessarily by all functions that are defined by means only of the function ![]() that has
that has ![]() . But these hereditary properties are not characteristic of all definable functions. In other words, there are definable functions that lack
. But these hereditary properties are not characteristic of all definable functions. In other words, there are definable functions that lack ![]() , for each hereditary property
, for each hereditary property ![]() . This explains Post’s result. A function that can indeed define, just by itself, all definable functions should not have any one of the hereditary properties because, if it had any such property, it would necessarily transmit it to every function it defines; but, then, the function could not define functions that lack this property.
. This explains Post’s result. A function that can indeed define, just by itself, all definable functions should not have any one of the hereditary properties because, if it had any such property, it would necessarily transmit it to every function it defines; but, then, the function could not define functions that lack this property.
Monotonicity:
Consider the case of binary functions, given the present inquiry. Note that these definitions of properties apply for n-ary functions in general. Note also that the two truth values
![]()
are ordered so that the truth value denoted by “F” is lower than that denoted by “T”. The table makes this point:

This is called partial ordering and, as a relation, it can be defined set-theoretically as:
![]()
A binary function
![]()
is monotonic if and only if, for all input values ![]() :
:
What does this mean in our case of binary logical connectives? There is a test, which follows from this definition, for determining whether a given binary connective is monotonic or not. The test goes like this. Start by writing out the input pairs for truth values (<![]() >) by using a diagram as shown below. This diagram arranges the pairs of truth values so that the arrows show the ordering just talked about. Next, write as a superscript for each pair of input values the truth value taken by the connective for that pair. For instance, for conjunction one has
>) by using a diagram as shown below. This diagram arranges the pairs of truth values so that the arrows show the ordering just talked about. Next, write as a superscript for each pair of input values the truth value taken by the connective for that pair. For instance, for conjunction one has
![]()
For the Sheffer Stroke (as can be checked from its truth table), one has:
![]()
There is failure of monotonicity if and only if there is at least one case in which one can proceed down the arrows from a T to an F superscript. This type of diagram is used below to show that the Sheffer Stroke is non-monotonic.
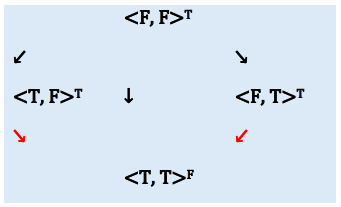
Since there are instances in which there is a shift in truth value of the connective from T to F as one goes down the red arrows, one can infer that this connective is not monotonic.
The set of monotonic unary or binary connectives is:
The Sheffer Stroke is not among them. Likewise, the Sheffer Stroke fails to be included among the other types of connectives identified above. And, so, by Post’s result, the Sheffer Stroke is functionally complete.
Linearity:
A logical connective is linear (also called countable, counting, or affine) if and only if it is the case that either all or none of the propositional inputs affect the truth value of the output. This means that for a linear connective, and only in the case of such a connective, for each of its inputs, changing the value of the input results in one of the following two cases: either the output value always changes or it never changes. For present purposes, concentrate on unary and binary connectives and proceed straight to presenting a test that can be used to determine whether a connective is linear or not. Here is how the test works: Check the cases in which the connectives takes T as its truth value. Call these the T-cases. Similarly, call the rest the F-cases. Then count the number of input variables that take T. If, and only if, the connective is linear, this number is always even for the T-cases and odd for the F-cases, or it is always odd for T-cases and even for the F-cases. One can show that this is not the case for the Sheffer Stroke. Hence, the Sheffer Stroke is not countable.
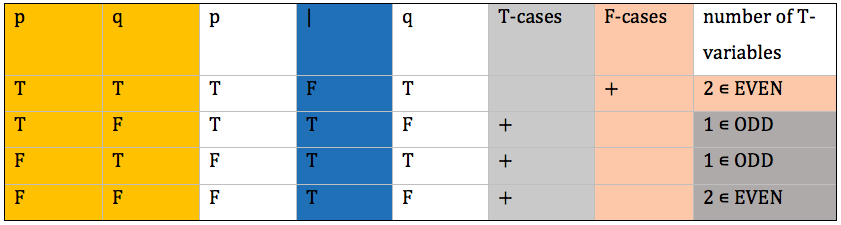
The rule is violated. The input variables that take T are even when the connective takes T as its truth value; but for the cases in which the connective takes F as its truth value, there is a mixture of even and odd numbers of input variables that are T. Hence, the Sheffer Stroke is not a linear connective.
The linear unary and binary connectives are as follows, and the Sheffer Stroke, again, is not among them.
Self-Duality:
Consider the case of unary and binary connectives. The dual of a unary or binary connective, (![]() and (
and (![]() respectively, can be defined as follows:
respectively, can be defined as follows:
![]()
Interestingly, the dual of the Sheffer Stroke is the other Sheffer function, NOR.
![]()
Now, a connective has the property of self-duality if and only if it is its own dual. As just seen, the dual of the Sheffer Stroke is the other Sheffer function, NOR; hence, the Sheffer Stroke does not have the property of self-duality. It is not among the members of the set of self-dual unary and binary connectives of the standard propositional logic.
Truth-Preservation and Falsehood-Preservation:
Finally, consider the two remaining properties of connectives, of interest for these purposes: truth-preservation and falsehood-preservation. It can be shown again that the Sheffer Stroke lacks these properties as well.
A connective is truth-preserving if and only if it yields the truth value T for all cases in which all its variable inputs are T.
In the general case of an n-ary connective, one has:
![]()
A connective is falsehood-preserving if and only if it yields the truth value F for all cases in which all its variable inputs are F.
![]()
The truth-preserving and falsehood-preserving unary and binary connectives of the standard propositional logic are given below, and, once again, the Sheffer Stroke is not among them.
The same tests could be applied on the other Sheffer function, the NOR connective, to show that this connective is also excluded from all these sets. No other unary or binary connectives would be excluded from all these sets. Therefore, the Sheffer Stroke and NOR are functionally complete and are the only connectives (among unary and binary connectives) that are functionally complete.
It can be shown that any logical connective, regardless of arity, is functionally complete if it has a property that is called complete symmetry. (see Bimbó, 1992)
It can then be ascertained that no unary connectives have this property and that the only binary connectives that have the property are the two Sheffer functions.
A binary logical connective
is completely symmetrical if and only if the following conditions hold. (“
” denotes truth value.)
In the literature, other functionally complete connectives (or, rather, their associated Boolean functions) are also called Sheffer functions. This applies in the case of non-standard or alternative logics, but these fall outside the scope of this article. In the case of the standard propositional logic, a Sheffer function is a function of any arity n (n ![]() 2) that is, taken by itself, functionally complete. The relevant fact to consider is this: Regardless of arity, a connective is functionally complete if it is completely symmetrical. This result applies only in the case of the standard (two-valued) propositional logic.
2) that is, taken by itself, functionally complete. The relevant fact to consider is this: Regardless of arity, a connective is functionally complete if it is completely symmetrical. This result applies only in the case of the standard (two-valued) propositional logic.
The definition of a completely symmetrical n-ary ![]() connective is now given:
connective is now given:
![]()
![]()
![]()
Here is a suggestive sketch of a proof of the fact that ![]() is functionally complete insofar as it is completely symmetrical. (see Bimbó, 1992)
is functionally complete insofar as it is completely symmetrical. (see Bimbó, 1992)
Assume a completely symmetrical n-ary connective, ![]() . Now, take the case of the truth table that can be constructed for
. Now, take the case of the truth table that can be constructed for
![]()
. This truth table must have only four rows, since there are exactly two propositional variables; it will have n columns since the function is n-ary.

Consider the results from the truth table above.
Since the connective is completely symmetrical, it must return or yield the same truth values (either T or F) for input values <T, F> and <F, T>. This yields exactly two cases: one in which the two truth values are T and one case in which the two truth values are both F. The first case has the truth table for the Sheffer Stroke; the second case has the truth table for the NOR connective. Thus,
In either case, the connective can be defined in terms of a functionally complete connective (either the Sheffer Stroke or NOR).
Accordingly, every definable function can be defined in terms of ![]() since
since ![]() is itself definable in terms of a functionally complete connective. This shows that
is itself definable in terms of a functionally complete connective. This shows that ![]() is itself functionally complete.
is itself functionally complete.
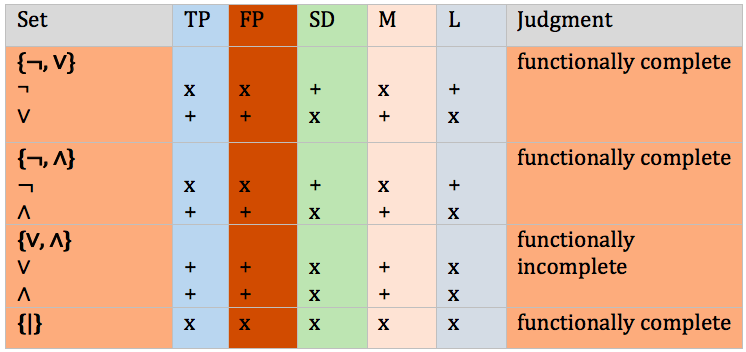
Apply the Post Test to determine whether a given set of functions is functionally complete,which means that by using only the functions in the set, all mathematically possible functions of the formal language can be defined. There are examples of sets of functions of the standard propositional logic, which are functionally complete, and one can see how the members of these sets lack, taken together, the hereditary properties discussed above. The Sheffer Stroke, and the Peirce Arrow, lack all those properties; therefore, the one-member sets that have as their single members the Sheffer Stroke or the Peirce Arrow are functionally complete. On the other hand, some sets are not functionally complete because some of the identified hereditary properties are not lacked by any one function in the given set. “TP” abbreviates “Truth-Preservativeness”, “FP” abbreviates “Falsehood-Preservativeness”, “SD” abbreviates “Self-Duality”, “M” abbreviates “Monotonicity”, and “L” abbreviates “Linearity.” Lacking the property is indicated by “x” while having the property is labeled by “+”. Thus, look for a set to have some “x” underneath each property across the row if this set is to be functionally complete.
It can be shown that the Sheffer Stroke possesses the property of functional completeness by examining its polynomial representation, which were introduced in section 1a; and the result is:
![]()
Linearity can be defined for the polynomial representations of the functions as absence of any multiplicational products from the polynomial. (This also means that all definable unary functions are linear since they have the general form
![]()
So, no unary function can be functionally complete since it has to be linear.) By examining the polynomial representation of the Sheffer Stroke we see that it is non-linear as it has a multiplicative product in it. Therefore, it lacks the hereditary property of linearity.
Next, show that it also lacks monotonicity.
![]()
![]()
Next, establish that the Sheffer Stroke is not self-dual. For a binary function in polynomial form, the self-duality condition can be given as follows.
![]()
![]()
In fact, the dual of the Sheffer Stroke is the other binary function that is functionally complete, the Peirce Arrow, whose polynomial representation is indeed:
![]()
.
Finally, it can be shown that the Sheffer Stroke is not truth-preserving and is not falsehood-preserving.
![]()
![]()
5. Significance of the Sheffer Stroke for Mathematical Logic, Philosophical Logic, and Philosophy
The significance of the Sheffer Stroke connective for mathematical logic and metalogic (the study of formal systems of logic) is evident from the observations made in the preceding section regarding the properties of this connective. Those properties are shared by its dual, the NOR connective. These two connectives are the only binary connectives that are functionally or expressively complete. They are also the first such connectives discovered to have this property as one ascends from zeroary or unary connectives. Examination of such properties belongs to what is known as Metalogic (sometimes called Metatheory). The possibility of economizing in the use of theoretical resources is greatly appealing to mathematicians and scientists. The principle widely known as Occam’s razor roughly states that stipulated entities should not be multiplied beyond the bare minimum of what is needed for a proposed theory to be fully constructible. Economy or parsimony with respect to the resources of a theory is considered a virtue and is demanded methodologically in the sense that, between two theories that have equal explanatory power and/or applications, the one that is more parsimonious should be adopted. It is not claimed that we have some independent insight into the subject addressed by the theories (for instance “nature” or a pre-theoretic structure of independent reality.) What is claimed is simply that parsimony or economy of resources is a methodological and theoretical requirement that good theories must meet.
Formal systems of logic, and formal languages, have expressive resources that are symbolic. Economic use of those resources means using in the construction and implementation of the theory as few such resources as is possible without loss of any systemic powers of expression. Ideally, economy dictates that only one resource of a certain kind is to be used, if such a resource is available or definable and is effective in the construction of all the remaining expressive resources. In the case of the connective symbols of a formal language of propositional logic, this reduction to one effective symbol proves to be feasible in the case of the standard propositional logic: hence, the revelatory significance of Sheffer’s discovery (which, as seen, had already been achieved by Peirce.) For the reduction to be effective, of course, it must be the case that all other connectives (of any arity ![]() ) must be definable in terms of the single connective symbol; in this way all the other connectives can be eliminated as expressive resources without causing a loss of the ability to express what those symbols refer to. Thus, for example, instead of “
) must be definable in terms of the single connective symbol; in this way all the other connectives can be eliminated as expressive resources without causing a loss of the ability to express what those symbols refer to. Thus, for example, instead of “![]() ”, one can write “
”, one can write “![]() ”, and the same for all other connective symbols.
”, and the same for all other connective symbols.
The advantages obtained from reduction of resources can be concrete in the case of implementations or applications of formal systems. For instance, in the construction of logic gates in electronic circuitry, the gate-types NAND and NOR are the electronic-theoretical interpretations of the same Boolean functions that are propositionally interpreted as the Sheffer connectives. As one ought to expect, NAND and NOR are universal gates. This means that any theoretically definable gate can be actually constructed from using just NAND gates or just NOR gates. Discoveries of this kind signal that a reduction in complexity is feasible, and this result can have economic and design advantages.
In practice, the advantage claimed from this reduction is outweighed by the fact that writing out well-formed expressions becomes prohibitively unwieldy if only one kind of connective symbol is used. For example, in the history of modern logic, Gottlob Frege’s notational variant never had a chance of being widely adopted because of the practically unmanageable demands it placed on typographical execution. One can think of this challenge as posing a trade-off between economy of resources and notational convenience. Or the trade-off is between reducing the type of resource (for instance, gate) used and needed, on the one hand, and the length or extension of the constructions that will have to be made, on the other. For example, to return to propositional logic, to express a well-formed formula like “![]() ” in terms of a single connective symbol,
” in terms of a single connective symbol, ![]() , one must write out the much longer equivalent well-formed formula shown below. The notational version being used in this way is significantly more unwieldy than a notational version (a grammar) that uses more, not fewer, connective symbols. Consider the formula
, one must write out the much longer equivalent well-formed formula shown below. The notational version being used in this way is significantly more unwieldy than a notational version (a grammar) that uses more, not fewer, connective symbols. Consider the formula
![]()
It is possible to adopt conventions that remove its complexity to some degree. For instance, stipulating that “![]() ” is to be written as “
” is to be written as “![]() ”, permits simplification of the formula above to
”, permits simplification of the formula above to
![]()
It is less obvious whether there is a deeper philosophical significance of the fact that a connective like Sheffer’s Stroke is available in a system of logic. Whitehead and Russell expressed boundless enthusiasm about Sheffer’s discovery, hinting only at an underlying significance of this while adopting the connective symbol in the second edition of Principia Mathematica. On the other hand, two other pioneering writers of logic textbooks, Hilbert and Ackermann, were unimpressed and reported on the Sheffer Stroke as if they were referring to trivia. Certainly, the Sheffer functions do not add to the logical system of standard propositional logic in any way. The simplification they make possible is an internal matter. If there are other logics for which, hypothetically, Sheffer functions are not available, this does not automatically mean that there is something wrong with those other systems insofar as they are assessed as formally constructed languages.
It was the influential thinker Ludwig Wittgenstein who attributed far-reaching significance to the fact that Sheffer functions are available. He did this in a somewhat obscure fashion in an influential logical-philosophical work.
a. Wittgenstein’s Tractatus and the Sheffer Stroke
In his Tractatus Logico-Philosophicus (1922, 5.1311, 6.001) Wittgenstein extolled the significance of the Sheffer functions, hinting that discovery of the functions vindicates some of the seminal claims he was raising in this famous text. It is not clear that Wittgenstein knew that there are two binary functions with the same property of being functionally complete. Wittgenstein’s connective symbol may appear, at first blush, to be the same symbol as NOR, which is the connective used by Sheffer himself in his alternative axiomatization of Huntington’s system. Wittgenstein’s connective has been mistaken as such even by Bertrand Russell, but this is a mistake. Wittgenstein uses a rather eccentric function, known in the literature as the N-operator, which has attracted attention and even led to disputes. Although this is not the place to enter into details, a few words are in order about Wittgenstein’s N-operator which is not the sentential NOR operator although it is inspired by it. A technical study of the subject is given by Soames (1983; see also Geach, 1981.)
Wittgenstein’s N-operator is defined over an open-ended set of propositional variables. Because the language that is needed is that of first-order or predicate logic, a propositional variable atom is a predicate symbol, of any arity n, accompanied by n individual constants all of which have as specified referents members of the universe of discourse (or domain.) It is an open problem for Wittgenstein’s language (whose grammar specification is rudimentary) that the domain set may or may not have a denumerably infinite number of subjects. Assuming a finitary domain for this brief excursion, and bear in mind that whatever fixes are available to address problems with Wittgenstein’s operator, are not efficient in the case of an infinite domain. Consider a grammar that comprises symbol letters for 22, individual constants, predicate (non-logical) constants, and the operator symbol. (These are not Wittgenstein’s symbols. Instead he legislates:
![]()
where the circumflex hints at the recursive mode of defining what expressions are grammatically correct. He uses “ξ” instead of “z” for molecular, not necessarily atomic, well-formed formulas.)
![]()
Then, application of the N-operator is, by definition, to negate all atomic propositions
![]()
in the set. This means that the N-operator can be defined through the following logical equivalences (insofar as the additional symbols are allowed in the metalanguage). The symbols for the existential and universal quantifier are “![]() ” and “
” and “![]() ”. These are missing from Wittgenstein’s language which is more parsimonious; but, as will be seen, Wittgenstein’s language, constructed on the N-operator, is expressively incomplete! Take, as example, the case of a unary predicate constant:
”. These are missing from Wittgenstein’s language which is more parsimonious; but, as will be seen, Wittgenstein’s language, constructed on the N-operator, is expressively incomplete! Take, as example, the case of a unary predicate constant:
![]()
One could then proceed to iterated applications of the N-operator, which will now give a clue as to how Wittgenstein’s operator is expressively incomplete.
![]()
The symbolic language cannot sort out more than one individual variable within the scope of another variable. It can express a formula like the following:
![]()
But the language lacks the resources to express formulas like the following, for which differentiation of individual variables within scopes is required:
![]()
![]()
Interestingly, the language also lacks resources for expressing ![]() . As Soames shows (1985), the defect can be remedied by adopting some additional symbolic convention that permits differentiation of individual variables within scopes. Thus, ironically, Wittgenstein’s constructed analogue to a Sheffer function, his N-operator, lacks expressive completeness. The set
. As Soames shows (1985), the defect can be remedied by adopting some additional symbolic convention that permits differentiation of individual variables within scopes. Thus, ironically, Wittgenstein’s constructed analogue to a Sheffer function, his N-operator, lacks expressive completeness. The set ![]() dispenses with the need for other connective symbols, and also for quantifier symbols (of which Wittgenstein thinks are defined through inclusive disjunction or conjunction, again disregarding the prospect of an infinite domain); yet, the language cannot express all constructible formulas of first-order logic. It was Moses Schöfinkel, the originator of combinatorial logic, (Bimbo, 2010) who constructed a functionally complete language for first-order logic using one Sheffer function.
dispenses with the need for other connective symbols, and also for quantifier symbols (of which Wittgenstein thinks are defined through inclusive disjunction or conjunction, again disregarding the prospect of an infinite domain); yet, the language cannot express all constructible formulas of first-order logic. It was Moses Schöfinkel, the originator of combinatorial logic, (Bimbo, 2010) who constructed a functionally complete language for first-order logic using one Sheffer function.
To conclude, consider the discussion of functional completeness, as touted by Wittgenstein in the Tractatus, putting aside the vicissitudes of his symbolic language. Although Wittgenstein claimed that the main subject of his Tractatus is ethical, the work examines a plethora of philosophical and logical subjects. An oft-discussed overriding objective of the work is to demarcate the limits of language; what cannot be expressed by language can be “shown,” as Wittgenstein famously claimed. The present subject fits within the Tractatus’ discussion of the nature of propositional logic and its relationship to the task of elucidation of meaning. (See Wittgenstein.)
Bursting into the scene on the heels of advances in modern logic made by Frege and Russell, the Tractatus is remarkable for its contributions to the philosophical discussion of the new logic as an instrument for clarification of logical meaning. Wittgenstein later abandoned the work’s objective of constructing an ideal formal language that would be “isomorphic” to the world of empirically ascertainable facts; he also moved away from a version of the Correspondence Theory of Truth that seems to be underpinning the Tractatus.
In the Tractatus, Wittgenstein explains that the logic of our theories about the world is not itself to be sought in the world. Let us assume that “A” symbolizes the proposition expressed by the sentence “snow is white” and “B” symbolizes the proposition “snow is a kind of precipitation.” Let us also assume for our present purposes that the truth or falsehood of propositions A and B are to be established by referring to empirical facts. It so happens in this example that both propositions, expressed by the two English sentences, are true in our actual, empirically accessible, world. Now form the compound proposition “A and B.” This new proposition must be true because both its component propositions are true. This is evident because the meaning of “and.” But how is this known? The empirical world itself does not come to our assistance. We know this regardless of empirical experience: what we know is that any compound proposition of the logical form “p and q” has to be true if, and only if, both of its components, the individual or atomic propositions p and q, are true. Thus, given p and q, the conclusion “p and q” follows validly: it is logically impossible to have a case in which the given premises are all true but the conclusion is false. Nevertheless, the logical meaning of any conjunctive proposition of the logical form “p and q” is identical with its truth conditions which comprises the determinate relations between truth value assignments to the components (whether p and q are true or false) the functionally determined truth value of the whole conjunction. Thus, the empirical fact that the conjunctive sentence is true in our actual world is irrelevant from the standpoint of the logical meaning (the truth conditions) of the logical form exemplified by the sentence “snow is white and snow is a form of precipitation.” The valuation dependency
![]()
is one of four logically possible combinations which comprise the truth conditions of the conjunctive logical form:
![]()
The actual world is not logically privileged, and Wittgenstein’s conceit that an isomorphic mapping can be accomplished, which would produce an ideal language of comprehensive applicability, was bound to be frustrated. Disregarding this rather metaphysical aspect, which Wittgenstein later also disregarded, the Tractatus contains an astute understanding and analysis of the formal logical instrument that has arisen out of modern mathematical developments. Wittgenstein’s contribution to the discussion of functional completeness fit under this aspect of the work.
Wittgenstein makes the point that “internal,” or “structural,” features of propositional forms account for truth preservation from the joint premises to the conclusion of a valid argument form. It is structural features that account, for instance, for the equivalence of logical meaning between any two propositions. This means that the propositions have forms that receive the same truth values for the same valuations (truth value assignments to their components.) Cases or valuations (also called interpretations and models) are determined by assigning truth values, true and false, to all the components of a propositional form. Wittgenstein uses the term “truth grounds” and “(logically) possible worlds” when referring to truth value assignments or valuations. Wittgenstein says that “these relations are internal and they exist as soon as, and by the very fact, that the propositions exist.” (1922, 5.13) The next thesis in Wittgenstein’s text (5.1311) is the one in which he uses his N-operator. The point made there is now presented roughly: having briefly examined the complications that arise out of Wittgenstein’s definition of an N-operator, one adjusts, instead, to a propositional language, pretending that Wittgenstein actually used the NOR function to make his case. Nothing is lost in this way because the point is to illustrate Wittgenstein’s remarks on the significance of functionally complete operators rather than to pursue further any details attaching to the N-operator itself.
Consider a valid argument form:
![]()
The usual name of this valid argument form is Disjunctive Syllogism. This is not a string of propositional forms; it is a schema, and so is something like a recipe for how to proceed correctly when drawing inferences. Wittgenstein makes the point that conventions of symbolism may create the wrong impression that there is no internal, structural connection running through all propositional forms; that there is something newly productive introduced by the multiple (connective) symbols. This, however, would be wrong. The accidental fact that many different symbols are used is what is misleading. Moreover, Wittgenstein has philosophical objections to working from the semantic side of constructing logical systems, and this has consequences for the subject under discussion. Wittgenstein considers semantic attempts to be nonsensical: for instance, to specify the referent of conjunction, in order to obtain a working semantics, commits one to the nonsense of speaking about extra-empirical items and, indeed, about things that cannot be talked about. This way of thinking shows certain underlying philosophical assumptions, which lie beyond this article’s scope, but the problem that arises is this: The construction of a logical system is to be understood as a matter of specifying formal-grammatical rules for concatenating and transforming the available symbolic resources of the system. Because of this, the failure of the grammatical or syntactical setup to show perspicuously what happens in logical operations is serious. Hence, it is imperative to show solely by manipulating the symbolic resources that there is an internal structural connection that relates all possible transformations. This is accomplished by using only one functionally complete operator symbol. This is the reason Wittgenstein extols the “discovery”. Even if one opts to multiply connective symbols, because of the greater simplicity and even intuitive appeal gained in that way, it is still crucial to be able to show that only one connective symbol suffices. Indeed, as is known from the above study of functional completeness, one could have opted for eliminating all but one connective symbol, one of the Sheffer functions. Consider further how the claim is to be made that single-connective symbolism reveals something deeper about logic itself.
Logical properties are structural features of the forms: thus, one can have tautologous, contradictory, and indeterminate (also called contingent and indefinite) propositional forms. All tautologies would have to have the same referent which, in the Fregean analysis, is the truth value true. If semantic referents are rejected, however, that leaves the grammatical means for showing the collapse of all tautologies, namely that they all have the logical meaning. The same is the case with all contradictory logical forms; they check as false for all logically possible assignments of values to their components. The remaining structural type, the contingent propositional form, is basically not logic’s business! This is indicated by the convention of assigning both truth values to a single propositional variable to generate two cases: these are two logically possible worlds if one is to semantically model the setup. The proposition can logically be true in one case and false in another; as a proposition it must be one or the other and it is not logically possible for it to be both true and false. Notice then that the two logical possibilities (p-T and p-F) have the same status. It does not matter if one of those, for an interpretation of the propositional symbol, happens to be the actual world. Logic, not depending on the workings of the empirical world, is attuned to characteristics that are invariable across all possible cases: this means, tautologies, which are true in all logically possible cases, and contradictions, which are false in all logically possible cases. The validity of the inferential schema above guarantees, for two-valued logic, that the following is a propositional tautology:
![]()
Once again, the proliferation of symbols obscures the facts about the internal structural simplicity of logic. All compound propositional forms are internally connected because they result from elementary propositional forms by means of connectives. The logic is determined by how the logical connectives are defined. Starting with elementary (also called individual or atomic) propositions, one always proceeds by combining them by means of connectives: the compounds generated are in every case dependent for their meanings (truth and falsehood) on the meanings (truth and falsehood) of their components. If one were to proceed in the opposite direction, from compounds toward the elementary propositions, there would be a decomposition of the compound propositions; the process would terminate with the elementary propositions. This is possible because all the connectives are truth-functional connectives. Thus, if, for instance, “p and q” is given as true, one can dissolve this into “p is true” and “q is true” given the definition of “and.” Once again, one sees that propositional forms are related with each other and, ultimately, they are related to two basic propositions, the true and the false, out of which any complex can be generated by using truth-functional connectives. This also shows that nothing in the logic of propositions can ever be arbitrary.
The symbolism that uses multiple connective symbols obscures this. A stronger point can be made: Something is wrong with a notational idiom, a symbolism, that fails to capture the identity of logical meanings (logical equivalence). For instance, consider the following two logically equivalent expressions or formulas, which are well-formed, it is assumed, in the idiom or notation (and represented here in the symbolically enriched metalanguage):
![]()
Even though the expressions are logically equivalent, the grammatically correct formulas representing them are not the same! This may be considered a radical notational or formal-grammatical defect. It gets even worse. There is a view that formalism is fundamentally a matter of systematic and specified manipulation of symbolic resources. Consequently, the defect faced in this case goes all the way to the roots of the most basic task of all: how to construct a faithful symbolic system relative to a given purpose. In that case, it would appear that the correct way to construct a formal system is exclusively through its minimally functionally complete sets of operators. If one has to switch to alternative idioms that have redundant operators in them (operators that can be defined by the other operators in the system), that would have to be justified by pleading such a reason as expediency or convenience.
The symbolic notation of a formal language idiom that uses only one connective symbol would remove this notational illusion, or, to make the stronger case, would remedy the deep formal-grammatical defect: then it could be perspicuously shown that all that is had is an unfolding of internal connections that run across propositional forms. Wittgenstein proceeds to write the above argument schema by using one single connective symbol which allows elimination of the symbols for disjunction and negation in order to make “the inner connection” obvious. (The contemporary symbol for the connective is the one used by Wittgenstein, which is NOR.)
![]()
To do this, replace “![]() ” by “
” by “![]() ” (thus eliminating the inclusive-disjunction symbol) and “
” (thus eliminating the inclusive-disjunction symbol) and “![]() ” by “
” by “![]() ” (thus eliminating the negation symbol). The NOR symbol is used to effect both eliminations. As a result, we have the schema shown above, in which only one connective symbol is used. Of course, one could have used the NAND or Sheffer Stroke function to effect the same elimination, in which case the result would be:
” (thus eliminating the negation symbol). The NOR symbol is used to effect both eliminations. As a result, we have the schema shown above, in which only one connective symbol is used. Of course, one could have used the NAND or Sheffer Stroke function to effect the same elimination, in which case the result would be:
![]()
Moreover, when multiple logical connectives are used in the construction of a formal system, an impression of arbitrariness may be created. Why, one may ask, is one set of logical connectives used instead of another set? The right answer is that nothing depends on which connectives are used because all the propositional formulas are internally related in strict, non-arbitrary fashion, and the construction ultimately depends on the basic building blocks and connectives. To illustrate this point, construct a formal system of the standard propositional logic by using as its set of connectives either
![]()
. Basically, it amounts to the same thing whichever one is used. This is not immediately obvious regarding the plurality of connectives seen above. But now consider how all of the connectives in these sets are definable in terms of the connective in ![]() . Thus,
. Thus, ![]() can be replaced by
can be replaced by ![]() ; and
; and ![]() can be replaced by
can be replaced by ![]() ; and
; and ![]() can be replaced by
can be replaced by ![]() . This fact makes clear that nothing depends on arbitrary choices about the connectives used. This discovery can be used as proof that there is a strict internal connection that runs through all the expressive resources.
. This fact makes clear that nothing depends on arbitrary choices about the connectives used. This discovery can be used as proof that there is a strict internal connection that runs through all the expressive resources.
Wittgenstein even points out (5.42) that having connectives in the formal system, which are interdefinable, means that they should not be properly regarded as “primitives.”
Now one can revisit the subject of the triviality of tautologies (and of logical contradictions), which is another subject on which Wittgenstein touches. There is one tautology, and a contradiction is the negation of the tautology (for the standard definition of negation.) Of course, negation itself can be expressed in terms of a Sheffer function. The ultimately perspicuous manifestation of the inner structural inter-connectedness of all logical propositions can be shown insofar as all valid tautologies can be derived from one single axiom that uses a single connective symbol. Rules of transformation and inference can be specified, to be applied to the axiom schema, to generate all valid tautologies. This is indeed possible, as French logician Jean Nicod (1917) demonstrated by constructing producing a one-postulate axiomatization of the standard propositional logic. Nicod’s postulate, written with metalinguistic symbols for writing a schema, is:
![]()
An alternative and equivalent formulation of the Nicod Postulate, which avoids having any sub-formulas of the postulate schema being tautologous, is the following. (Notably, in the original formulation, the sub-formula ![]() is tautologous.)
is tautologous.)
![]()
The Nicod Postulate can be deployed as the single axiom in a formal system whose only rule of inference is given by the following rule schema:
![]()
6. References and Further Reading
- Béziau, Jean-Yves. 2001. “Sequents and Bivaluations”, Logique et Analyse 176, pp. 373-94.
- Bimbó, Katalin. 2010. “Schöfinkel-Type Operators for Classical Logic”, Studia Logica 95: 355-78.
- Church, Alonzo. 1996. Introduction to Mathematical Logic, revised and enlarged edition,
Princeton: Princeton University Press. - Church, Alonzo. 1953. “Review of Sobociński (1953), Journal of Symbolic Logic 18: 284-85.
- Geach, P. T. 1981. “Wittgenstein’s Operator N”, Analysis 41: 168-71.
- Goodell, John D. and Tenny Lode. 1953. “Decision Elements”, Journal of Symbolic Logic 18:
283-84. - Hilbert, D., and W. Ackermann. 1928. Grundzüge der theoretischen Logik. Berlin: Springer.
- Houser, N., Roberts, Don D., and Van Evra, James (eds.). 1997. Studies in the Logic of Charles Sanders Peirce. Bloomington, IN: Indiana University Press.
- Nicod, Jean G. P. 1917. “A Reduction in the Number of Primitives Propositions of Logic”, Proceedings of the Cambridge Philosophical Society 19: 32-41.
- Peirce, Charles S. 1931-1966. Collected Papers of Charles Sanders Peirce. 8 volumes, ed. by
Hartshorne, C, Weiss, P. and Burks, A. W.. Cambridge, MA: Harvard University Press. - Peirce, Charles S. 1967. “Annotated Catalogue of the Papers of Charles S. Peirce”,
Manuscripts in the Houghton Library of Harvard University, as identified by Richard
Robin. Amherst: University of Massachusetts Press. - Peirce, Charles, S. 1971. “The Peirce Papers: A supplementary catalogue”, Transactions of
the C. S. Peirce Society 7: 37–57. - Pelletier, Jeffrey Francis and Norman M. Martin. 1990. “Post’s Functional Completeness
Theorem”, Notre Dame Journal of Formal Logic 31: 462-75. - Post, Emil L. 1921. “Introduction to a General Theory of Elementary Propositions”, American Journal of Mathematics 43: 163-85.
- Post, Emil L. 1941. The Two-Valued Iterative Systems of Mathematical Logic, vol. 5 of Annals of Mathematical Studies, Princeton: Princeton University Press.
- Prior, Arthur N. 1962. Formal Logic. Oxford: Clarendon Press.
- Quine, Willard Van O. 1995. Selected Logic Papers, enlarged edition, Cambridge, MA:
Harvard University Press. - Read, Steven. 1999. “Sheffer’s Stroke: A Study in Proof-Theoretic Harmony”, Danish
Yearbook of Philosophy 34: 7-24. - Riser, John. 1967. “A Gentzen-Type Calculus for Sequents for Single-Operator Propositional
Logic”, The Journal of Symbolic Logic 32: 75-80. - Sheffer, H. M. 1913. “A Set of Five Independent Postulates for Boolean Algebras, with
Application to Logical Constants”, Transactions of the American Mathematical Society 14: 481-88. - Soames, Scott. 1983. “Generality, Truth Functions, and Expressive Capacity in the Tractatus”, The Philosophical Review 92: 573-89.
- Sobociński, Bolesław, 1953. “On a Universal Decision Element”, Journal of Computing Systems 1: 71-80.
- Wernick, William. 1942. “Complete Sets of Logical Functions”, Transactions of the American
Mathematical Society 51: 117-32. - Whitehead, Alfred and Bertrand Russell. 1910, 1912, 1913. Principia Mathematica, 3
volumes. Cambridge: Cambridge University Press; 1925, 1927. Principia Mathematica, second edition, 2 volumes, Cambridge: Cambridge University Press. - Wittgenstein, Ludwig. 1922. Tractatus Logico-Philosophicus, tr. C.K. Ogden. London:
Routledge & Kegan Paul.
Author Information
Odysseus Makridis
Email: makridis@fdu.edu
Fairleigh Dickinson University
U. S. A.
